Giải bài tập SGK Tin học 10 Bài 4: Bài toán và thuật toán
Để các em có thêm nhiều tài liệu tham khảo hữu ích cho môn Tin học 10, đội ngũ eLib xin giới thiệu đến các em học sinh nội dung giải bài tập SGK bên dưới đây. Tài liệu được biên soạn gồm 7 câu hỏi trang 44 có phương pháp và lời giải đi kèm. Mời các em cùng theo dõi!
Mục lục nội dung

1. Giải bài 1 trang 44 SGK Tin học 10
Hãy phát biểu một bài toán và chỉ rõ Input và Output của bài toán đó.
Phương pháp giải
Dựa vào hiểu biết của bản thân và nội dung mục 1 khái niệm bài toán được trình bày ở trang 32 SGK Tin học 10 để phân tích và đưa ra câu trả lời phù hợp.
Hướng dẫn giải
Ví dụ Bài toán Tính diện tích tam giác
Phát biểu bài toán: Cho ba cạnh của tam giác ABC là: X, Y, Z. Hãy tính diện tích tam giác ABC.
- Input: Ba cạnh tam giác X, Y, Z
- Output: Diện tích tam giác
2. Giải bài 2 trang 44 SGK Tin học 10
Dãy các thao tác sau:
Bước 1. Xóa bảng;
Bước 2. Vẽ đường tròn;
Bước 3. Quay lại bước 1.
Có phải là thuật toán không? Tại sao?
Phương pháp giải
Từ các kiến thức đã học và nội dung mục 2 khái niệm thuật toán được trình bày ở trang 33 SGK Tin học 10 để phân tích và đưa ra câu trả lời phù hợp.
Hướng dẫn giải
Dãy các thao tác trên không phải là thuật toán, vì không thoả mãn tính chất dừng: đến bước 3 lại quay lại bước 1, nó tạo thành vòng lặp vô hạn không có điều kiện kết thúc.
3. Giải bài 3 trang 44 SGK Tin học 10
Hãy chỉ ra tính dừng của thuật toán tìm kiếm tuần tự.
Phương pháp giải
Dựa vào hiểu biết của bản thân và nội dung mục 2 khái niệm thuật toán được trình bày ở trang 33,34 SGK Tin học 10 để trả lời.
Hướng dẫn giải
- Thuật toán tìm kiếm tuần tự:
+ Bước 1: Nhập N, các số hạng a1, a2,…, aN và giá trị khoá k;
+ Bước 2: i ← 1
+ Bước 3: Nếu ai = k thì thông báo chỉ số i, rồi kết thúc;
+ Bước 4: i ← i +1
+ Bước 5: Nếu i > N thì thông báo dãy A không có số hạng nào có giá trị bằng k, rồi kết thúc;
+ Bước 6: Quay lại bước 3;
- Tính dừng của thuật toán tìm kiếm tuần tự: nghĩa là thuật toán phải kết thúc sau một số hữu hạn lần bước tính.
+ Thuật toán chia làm hai trường hợp:
Nếu tìm thấy giá trị cần tìm trong dãy A (ai= k) thì thông báo chỉ số i (vị trí tìm thấy khoá k trong dãy A), rồi kết thúc
Nếu không tìm thấy giá trị cần tìm trong dãy A, vì bước 4 thực hiện việc tăng giá trị của i lớn hơn 1, nên sau N lần thì i > N, thông báo dãy A không có giá trị nào bằng k, rồi kết thúc
4. Giải bài 4 trang 44 SGK Tin học 10
Cho N và dãy số a1....aN, hãy tìm giá trị nhỏ nhất (Min) của dãy đó.
Hãy mô tả thuật toán giải bài toán trên bằng cách liệt kê hoặc bằng sơ đồ khối.
Phương pháp giải
Từ nội dung mục 3 SGK Tin học 10 trang 36 để phân tích và đưa ra câu trả lời phù hợp với đề bài.
Hướng dẫn giải
- Xác định bài toán:
+ Input: Số N và dãy N số a1, a2, ...,aN.
+ Output: Giá trị nhỏ nhất (Min) của dãy số.
- Ý tưởng:
+ Khởi tạo giá trị Min = a1
+ Lần lượt nhận giá trị i chạy từ 2 đến N, so sánh giá trị số hạng a1 với giá trị Min, nếu ai < Min thì Min nhận giá trị mới ai
- Thuật toán:
+ Mô tả thuật toán theo cách liệt kê:
- Bước 1: Nhập N và dãy a1,…, aN;
- Bước 2: Min ← a1; i ← 2;
- Bước 3: Nếu i > N thì đưa ra giá trị Min rồi kết thúc;
- Bước 4: Nếu ai < Min thì Min ← ai; i ← i+1 rồi quay lại Bước 3
- Mô tả thuật toán bằng sơ đồ khối:
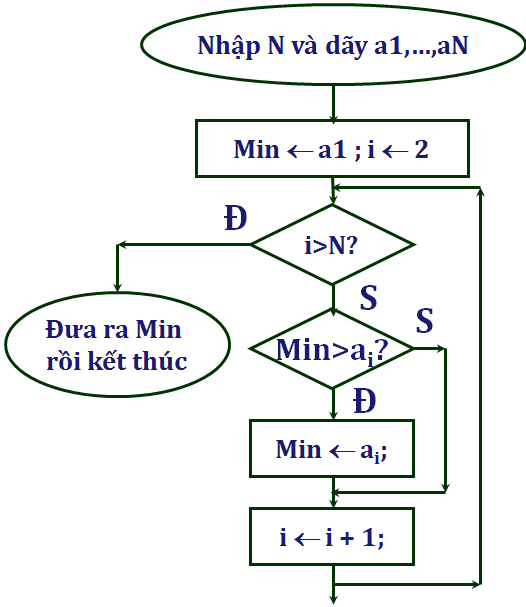
5. Giải bài 5 trang 44SGK Tin học 10
Tìm nghiệm của phương trình bậc hai tổng quát: ax2+bx+c=0. Hãy mô tả thuật toán giải bài toán trên bằng cách liệt kê hoặc bằng sơ đồ khối.
Phương pháp giải
Dựa vào các kiến thức đã học và nội dung chính được trình bày mục 3 một số ví dụ về thuật toán được trình bày ở trang 36 SGK Tin học 10 để phân tích và đưa ra câu trả lời phù hợp.
Hướng dẫn giải
- Xác định bài toán:
+ Input: Các số thực a, c, c (a≠0)
+ Output: Các số thực X thoả mãn ax2 + bx + c = 0
- Ý tưởng:
+ Tính D = b2 - 4ac
+ Lần lượt xét ba trường hợp cho giá trị D:
+ Nếu D < 0 thì phương trình vô nghiệm
+ Nếu D = 0 thì kết luận phương trình có một nghiệm x =-b/2a
+ Nếu D > 0 thì kết luận phương trình có hai nghiệm phân biệt là: x1, x2 = (-b ± \(\sqrt{D}\))/2a
- Mô tả thuật toán bằng cách liệt kê:
+ Bước 1: Nhập a, b, c;
+ Bước 2: Tính D = b2 - 4ac;
+ Bước 3: Nếu D < 0 → phương trình vô nghiệm \(\rightarrow\) Bước 6;
+ Bước 4: Nếu D = 0 → phương trình có nghiệm kép x = -b/2a → Bước 6;
+ Bước 5: Nếu D > 0 → phương trình có hai nghiệm x1, x2 = (-b ± \(\sqrt{D}\))/2a → Bước 6;
+ Bước 6: Kết thúc.
- Mô tả thuật toán bằng sơ đồ khối:
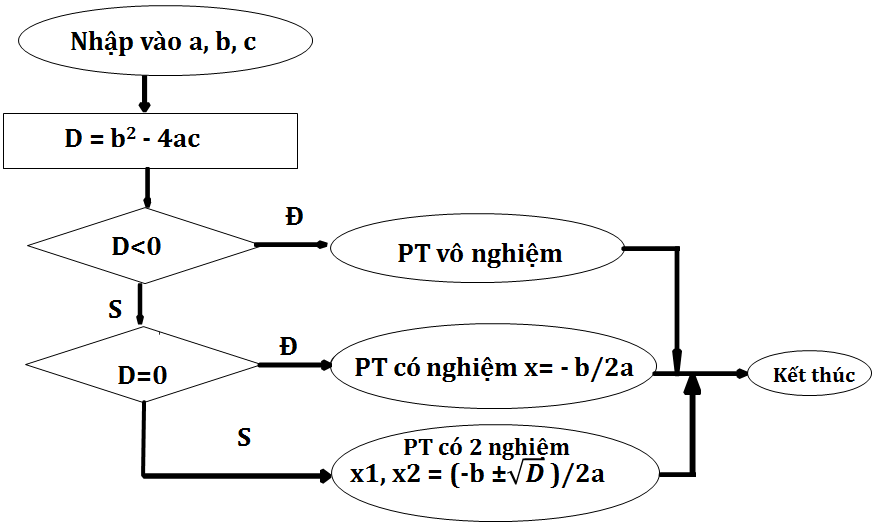
6. Giải bài 6 trang 44 SGK Tin học 10
Cho N và dãy số a1... aN, hãy sắp xếp dãy số đó thành dãy số không tăng (số hạng trước lớn hơn hay bằng số hạng sau). Hãy mô tả thuật toán giải bài toán trên bằng cách liệt kê hoặc bằng sơ đồ khối.
Phương pháp giải
Từ vào hiểu biết của bản thân và nội dung mục 3 được trình bày ở trang 36 SGK Tin học 10 để trả lời.
Hướng dẫn giải
- Xác điịnh bài toán
+ Input: Dãy A gồm N số nguyên a1, a2..., aN
+ Output: Dãy A được sắp xếp lại thành dãy không tăng
- Ý tưởng: Với mỗi cặp số hạng đứng liền kề trong dãy, nếu số trước nhỏ hơn số sau ta đổi chỗ chúng cho nhau. Việc đó được lặp lại, cho đến khi không có sự đổi chỗ nào xảy ra nữa.
- Mô tả thuật toán bằng cách liệt kê:
+ Bước 1. Nhập N, các số hạng a,,a2..., aN;
+ Bước 2: M ← N ;
+ Bước 3: Nếu M < 2 thì đưa ra dãy A đã được sắp xếp rồi kết thúc;
+ Bước 4: M ← M-1, i ← 0
+ Bước 5: i ← i+1
+ Bước 6: Nếu i>M thì quay lại bước 3
+ Bước 7: Nếu ai < ai+1 thì tráo đổi ai và ai+1 cho nhau
+ Bước 8: Quay lại Bước 5
7. Giải bài 7 trang 44 SGK Tin học 10
Cho N và dãy số a1....aN, hãy cho biết có bao nhiêu số hạng trong dãy có giá trị bằng 0. Hãy mô tả thuật toán giải bài toán trên bằng cách liệt kê hoặc bằng sơ đồ khối.
Phương pháp giải
Từ các kiến thức đã học kết hợp với nội dung mục 3 một số ví dụ về thuật toán được trình bày ở SGK Tin học 10 để giải quyết bài tập này.
Hướng dẫn giải
- Xác định bài toán
+ Input: Dãy A gồm N số nguyên a1, a2..., aN ;
+ Output: Số số hạng trong dãy A có giá trị bằng 0.
- Ý tưởng: Tìm kiếm tuần tự được thực hiện một cách tự nhiên. Ta dùng biến dem để đếm số số hạng trong dãy A có giá trị bằng 0. Bắt đầu từ i = 1 và mỗi lần tăng i lên 1, ta lần lượt so sánh ai = 0?, nếu ai = 0 thì tăng dem lên 1, tiếp tục quá trình cho đến khi i > N thì đưa ra kết quả dem và kết thúc.
- Mô tả thuật toán bằng cách liệt kê:
+ Bước 1: Nhập N, dãy a1,..,aN
+ Bước 2: i:=1; dem:=0
+ Bước 3: Nếu i>N thì đến Bước 5
+ Bước 4: Nếu a[i]=0 thì dem:=dem+1; i:=i+1 quay lại Bước 3
+ Bước 5: Thông báo kết quả la dem
- Mô tả thuật toán bằng cách sơ đồ khối:
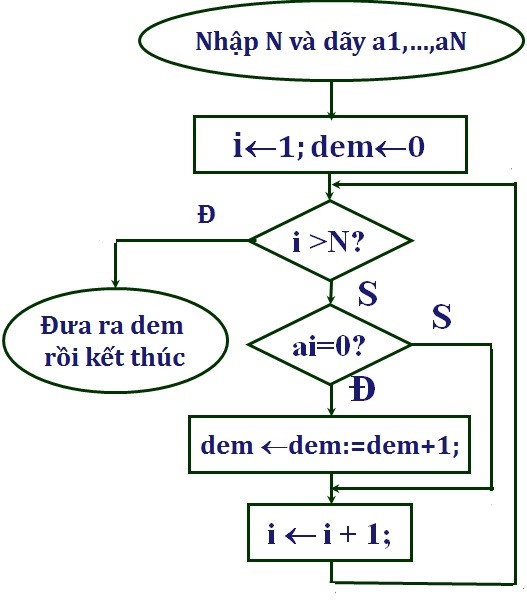
Tham khảo thêm
- doc Giải bài tập SGK Tin học 10 Bài 1: Tin học là một ngành khoa học
- doc Giải bài tập SGK Tin học 10 Bài tập và thực hành 1: Làm quen với thông tin và mã hóa thông tin
- doc Giải bài tập SGK Tin học 10 Bài 3: Giới thiệu về máy tính
- doc Giải bài tập SGK Tin học 10 Bài 5: Ngôn ngữ lập trình
- doc Giải bài tập SGK Tin học 10 Bài 6: Giải bài toán trên máy tính
- doc Giải bài tập SGK Tin học 10 Bài 7: Phần mềm máy tính
- doc Giải bài tập SGK Tin học 10 Bài 8: Những ứng dụng của tin học
- doc Giải bài tập SGK Tin học 10 Bài 9: Tin học và xã hội
