Bài 9: Kiểm định giả thiết về tính độc lập
Nội dung bài giảng Lý thuyết xác suất thống kê Bài 9: Kiểm định giả thiết về tính độc lập sau đây sẽ giúp các bạn tìm hiểu về tính độc lập với các ví dụ minh họa cụ thể. Cùng eLib tham khảo nhé!

Giả sử quan sát đồng thời hai dấu hiệu A và B trên cùng một phần tử.
Dấu hiệu A có các dấu hiệu thành phần là: \(A_1, A_2,..., A_h\);
Dấu hiệu B có các dấu hiệu thành phần là: \( B_1, B_2,..., B_k\)
Ta cần kiểm định giả thiết:
H0: A và B độc lập; H1: A và B không độc lập.
Lấy mẫu kích thước n và trình bày kết quâ quan sát dưới dạng bảng sau đây:
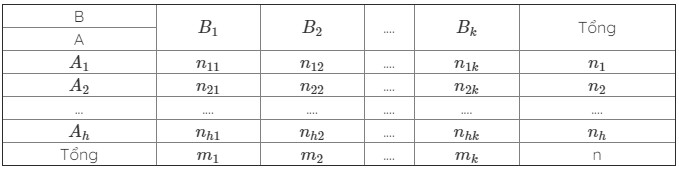
Trong đó:
\({n_i} = \left( {i = \overline {1,h} } \right)\) là tổng số phần tử mang dấu hiệu thành phần Ai.
\({m_j} = \left( {j = \overline {1,k} } \right)\) là tổng số phần tử mang dâu hiệu thành phần Bj
\({n_{{\rm{ij}}}}{\rm{ }}\left( {i = \overline {1,h} ,{\rm{ }}j = \overline {1,k} } \right)\) là tổng số phần tử mang dấu hiệu thành phần Ai và Bj.
Gọi Ci là biến cố chọn được phần tử mang dấu hiệu Ai
Dj là biến cố chọn được phần tử mang dấu hiệu Bj
Khi n khá lớn, theo định nghĩa thống kê về xác suất ta có:
\(P\left( {{C_i}{D_j}} \right) = \frac{{{n_{{\rm{ij}}}}}}{n};\,\,\,\,P\left( {{C_i}} \right) = \frac{{{n_{\rm{i}}}}}{n};\,\,\,\,P\left( {{D_j}} \right) = \frac{{{m_{\rm{j}}}}}{n};\)
Nếu H0 đúng, tức A, B độc lập thì các dấu hiệu Ai, Bj cũng độc lập. Do đó:
\(P({C_i}.{D_j}) = P\left( {{C_i}} \right)P\left( {{D_j}} \right)\)
Tức là:
\(\frac{{{n_{{\rm{ij}}}}}}{n} = \frac{{{n_{\rm{i}}}}}{n}.\frac{{{m_{\rm{j}}}}}{n}\)
Từ đó ta có qui tắc quyết định như sau:
- Lấy mẫu kích thước n, từ mẫu này tính:
\({\chi ^2} = \sum\limits_{i = 1}^h {\sum\limits_{j = 1}^k {\frac{{{{\left( {\frac{{{n_{{\rm{ij}}}}}}{n} - \frac{{{n_{\rm{i}}}}}{n}.\frac{{{m_{\rm{j}}}}}{n}} \right)}^2}}}{{\frac{{{n_{\rm{i}}}}}{n}.\frac{{{m_{\rm{j}}}}}{n}}}} } = n\left( {\sum\limits_{i = 1}^h {\sum\limits_{j = 1}^k {\frac{{n_{{\rm{ij}}}^2}}{{{n_i}.{m_j}}} - 1} } } \right)\)
- Với mức ý nghĩa a đã cho, tra bảng \({\chi ^2}\) với bậc tự do \((k-1)(h-1)\) để tìm \(\chi _\alpha ^2\) (hoặc dùng hàm CHIINV trong Excel). Nếu \({\chi ^2} > \chi _\alpha ^2\) thì bác bỏ H0, thừa nhận H1 Nếu \({\chi ^2} \le \chi _\alpha ^2\) thì có thể chấp nhận H0
Thí dụ: Làm thí nghiệm bón một loại phân theo 3 phương pháp khác nhau cho cùng một loại cây trồng và quan sát việc ra hoa của loại cây này, ta có kết quả cho ở bảng sau:

Với mức ý nghĩa \(\alpha = 0,05\) hãy kết luận xem phương pháp bón phân khác nhau có ảnh hưởng tới việc ra hoa của loại cây đó không ?
Giải:
Đặt giả thiết H0: Phương pháp bón phân (dấu hiệu A) độc lập với việc ra hoa của cây (dấu hiệu B).
H1: Phương pháp bón phân không độc lập (có ảnh hưởng) đến việc ra hoa của cây.
Từ bảng số liệu đã cho, để tính \({\chi ^2}\) trước hết ta tính các số hạng:
\({\alpha _{{\rm{ij}}}} = \frac{{n_{{\rm{ij}}}^2}}{{{n_i}{m_j}}}\,\,\,\,(\forall i,j)\)
Ở thí dụ ta đang xét, ứng với ô có \(n_{ij}=40\) (tức i = 1 và j = 1) thì:
\({\alpha _{11}} = \frac{{n_{{\rm{11}}}^2}}{{{n_1}{m_1}}}\,\,\, = \frac{{{{40}^2}}}{{178.55}} = 0,163432\)
Ứng với ô có \(n_{ij}=75\) (tức i = 1 và j = 2) thì:
\({\alpha _{12}} = \frac{{n_{12}^2}}{{{n_1}{m_2}}}\,\,\, = \frac{{{{75}^2}}}{{178.87}} = 0,363231\)
Đối với các ô còn lại ta cũng tính tương tự. Kết quả tính toán được trình bày dưới dạng bảng như sau:
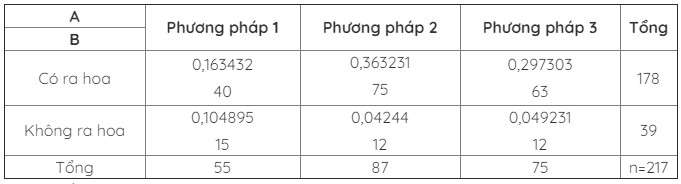
Từ các kết quả tính ở bảng trên, ta tính được:
\(\sum\limits_{i = 1}^h {\sum\limits_{j = 1}^k {\frac{{n_{{\rm{ij}}}^2}}{{{n_i}.{m_j}}}} } = 0,163432 + 0,363231 +... + 0,049231 = 1,020533\)
Vậy:
\({\chi ^2} = n\left( {\sum\limits_{i = 1}^h {\sum\limits_{j = 1}^k {\frac{{n_{{\rm{ij}}}^2}}{{{n_i}.{m_j}}}} } - 1} \right) = 217(1,020533 - 1) = 4,45565\)
Với mức ý nghĩa \(\alpha = 0,05\), tra bảng \({\chi ^2}\) với bậc tự do:
\(V = (h - 1).(k - 1) = (3 - 1).(2 - 1) = 2\)
ta được:
\(\chi _\alpha ^2 = \chi _{0,05}^2 = 5,991\)
Vì \(\chi _\alpha ^2 = 4,45565 < \chi _{0,05}^2 = 5,991\), nên ta chấp nhận giả thiết H0, tức phương pháp bón phân không ảnh hưởng đến việc ra hoa của loại cây này.
Trên đây là nội dung bài giảng Bài 9: Kiểm định giả thiết về tính độc lập mà eLib.VN muốn chia sẻ đến các bạn sinh viên. Hy vọng đây sẽ là tư liệu hữu ích giúp các bạn nắm được nội dung bài học tốt hơn. Chúc các bạn học tốt.
Tham khảo thêm
- doc Bài 1: Các khái niệm Kiểm định giả thiết thống kê
- doc Bài 2: Kiểm định giả thiết phương pháp khoảng tin cậy và trung bình của tổng thể
- doc Bài 3: Kiểm định giả thiết bằng p-value
- doc Bài 4: Tính xác suất sai lầm loại 2
- doc Bài 5: Kiểm định giả thiết về tỷ lệ tổng thể và sự bằng nhau của hai trung bình
- doc Bài 6: Kiểm định giả thiết về sự bằng nhau của hai tỷ lệ và phương sai của tổng thể
- doc Bài 7: Kiểm định giả thiết về sự bằng nhau của hai phương sai
- doc Bài 8: Kiểm định giả thiết về phân phối xác suất của đại lượng ngẫu nhiên
