Lý 10 Bài 31: Phương trình trạng thái của khí lí tưởng
Chúng ta xác định mối liên hệ giữa 3 thông số trạng thái: áp suất, thể tích và nhiệt độ tuyệt đối thông qua phương trình nào? Để trả lời cho câu hỏi trên, mời các em cùng theo dõi nội dung bài học dưới đây. Chúc các em học tốt!
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Khí thực và khí lí tưởng.
- Khí thực:
- Khí thực là chất khí tồn tại trong thực tế như (oxi, nitơ, cacbonic,....)
- Khi không yêu cầu độ chính xác cao, ta có thể áp dụng các định luật về chất khí lí tưởng để tính áp suất, thể tích và nhiệt độ của khí thực.
- Khí lí tưởng:
- Khí lí tưởng là tuân theo đúng các định luật về chất khí đã học.
- Khí lí tưởng tuân theo đúng các định luật Bôi-lơ- Ma-ri-ốt và Sác- lơ, còn khí thực chỉ tuân theo gần đúng các định luật này.
1.2. Phương trình trạng thái của khí lí tưởng.
-
Xét một lượng khí chuyển từ trạng thái 1 \(({p_1},{\rm{ }}{V_1},{\rm{ }}{T_1})\) sang trạng thái 2 \(({p_2},{\rm{ }}{V_2},{\rm{ }}{T_2})\) qua trạng thái trung gian 1’ \((p,{\rm{ }}{V_2},{\rm{ }}{T_1})\) :
-
Quá trình đi từ 1 → 1’: đẳng nhiệt
\({p_1}{V_{1}} = p.{V_2}\) (1)
-
Quá trình đi từ 1’ → 2 : đẳng tích
\(\frac{{p'}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}}\) (2)
- Từ (2) \( \to P'\) rồi thế vào (1)
- Ta có : \(\frac{{{P_1}{V_1}}}{{{T_1}}} = \frac{{{P_2}{V_2}}}{{{T_2}}}\) hay \(\frac{{p.V}}{T} = \) hằng số
- Độ lớn của hằng số này phụ thuộc vào khối lượng khí.
- Phương trình trên do nhà vật lí người Pháp Cla- pê- rôn đưa ra vào năm 1834 gọi là phương trình trạng thái của khí lí tưởng hay phương trình Cla- pê- rôn.
1.3. Quá trình đẳng áp
a) Quá trình đẳng áp
Quá trình đẳng áp là quá trình biến đổi trạng thái khi áp suất không đổi.
b) Liên hệ giữa thể tích và nhiệt độ tuyệt đối trong quá trình đẳng áp
Từ phương trình trạng thái:
\(\frac{{{P_1}{V_1}}}{{{T_1}}} = \frac{{{P_2}{V_2}}}{{{T_2}}}\) nếu \({P_1} = {P_2}\) nghĩa là áp suất không đổi, ta có:
\(\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_2}}}{{{T_2}}} \to \frac{V}{T} = \) hằng số
⇒ Trong quá trình đẳng áp của một lượng khí nhất định, thể tích tỉ lệ thuận với nhiệt độ tuyệt đối.
c) Đường đẳng áp
- Đường biểu diễn sự biến thiên của thể tích theo nhiệt độ khi áp suất không đổi gọi là đường đẳng áp.
- Đặc điểm:
- Đường thẳng có đường kéo dài đi qua gốc tọa độ trong hệ tọa độ(V,T)
- Đường ở trên ứng với áp suất nhỏ hơn ở đường bên dưới
- Dạng đường đẳng áp :
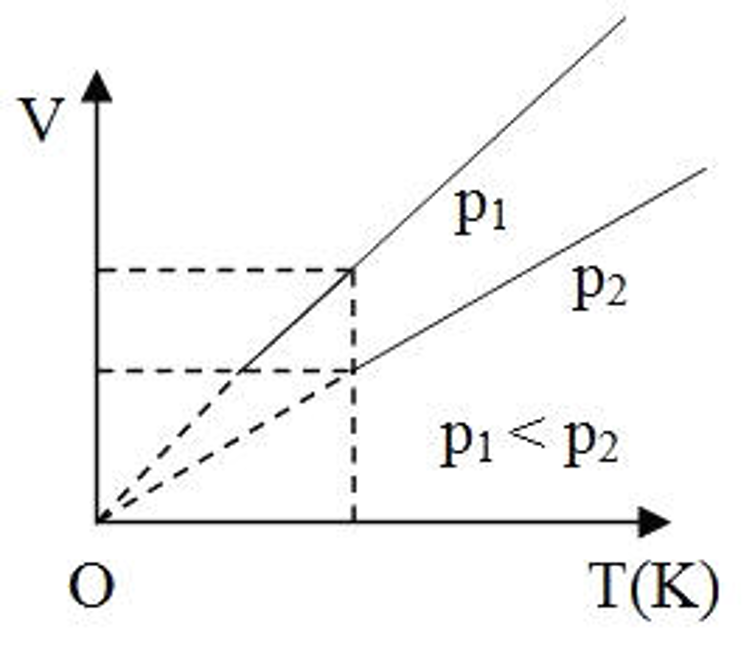
-
Trong hệ toạ độ OVT đường đẳng áp là đường thẳng kéo dài đi qua góc toạ độ.
-
Ứng với các thể tích khác nhau của cùng một lượng khí ta có những đường đẳng áp khác nhau. Đường ở trên có áp suất nhỏ hơn.
1.4. Độ không tuyệt đối.
- Ý nghĩa : Khi T=0 K => p=0 và V=0. Điều đó thực tế chỉ có thể gần đạt được mà thôi. Vì nếu đạt được thì vật chất ngừng hoạt động, nghĩa là trái với quy luật vận đọng cảu vật chất .
- Nhiệt giai Kevin: Nhiệt giai bắt đầu nhiệt độ bằng 0 K gọi là “Độ không tuyệt đối”. Các nhiệt độ trong nhiệt giai Kevin đều có giá trị dương và mỗi độ chai tỏng nhiệt giai này cũng bằng mỗi độ chia trong nhiệt giai Celsius.
→ Không thể đạt tới 0 K và 0 K gọi là độ không tuyệt đối.
2. Bài tập minh họa
2.1. Dạng 1: Xác định khối lượng riêng của không khí
Tính khối lượng riêng của không khí ở đỉnh núi Phăng-xi-păng cao 3 140 m. Biết rằng mỗi khi lên cao thêm 10 m thì áp suất khí quyển giàm 1 mmHg và nhiệt độ trên đỉnh núi là 20C. Khối lượng riêng của không khí ở điều kiện chuẩn (áp suất 760 mmHg và nhiệt độ 00C) là 1,29 kg/m3 .
Hướng dẫn giải
Cứ lên cao thêm 10 m thì áp suất khí quyển giảm 1mmHg.
⇒ Ở độ cao 3140 thì áp suất khí quyển giảm 312 mmHg.
⇒ Áp suất của khí quyển ở đỉnh núi Phan - xi - păng là: 760 - 314 = 446 mmHg.
Trạng thái 1:
\(p_1 = 760 – 314 = 446 mmHg\); \(T_1 = 273 + 2 = 275 K\); V1, D1
Trạng thái 2:
\(p_0 = 760 mmHg\); \(T_0 = 273 K\); V0; D0 = 1,29 kg/m3
Phương trình trạng thái khí lí tưởng:
\(\frac{{{p_0}{V_0}}}{{{T_0}}} = \frac{{pV}}{T_1} \Rightarrow \frac{{{V_0}}}{V_1} = \frac{P_1}{{{P_0}}}.\frac{{{T_0}}}{T_1}= \frac{{446.273}}{{760.275}} = 0,583\)
Lại có:
\( V_{0}=\frac{m}{D_{0}} ; V_{1}=\frac{m}{D_{1}} \)
\( \Rightarrow \frac{V_{0}}{V_{1}}=\frac{\frac{m}{D_{0}}}{\frac{m}{D_{1}}}=\frac{D_{1}}{D_{0}} \)
\( \Rightarrow D_{1}=D_{0} \cdot \frac{V_{0}}{V_{1}}=1,29.0,5826=0,75\left(\mathrm{kg} / \mathrm{cm}^{3}\right) \)
Vậy, khối lượng riêng của không khí ở đỉnh núi Phăng-xi-phăng là: \(D_{1}= 0,75\left(\mathrm{kg} / \mathrm{cm}^{3}\right) \)
2.2. Dạng 2: Tìm thể tích của lượng khí
Trong phòng thí nghiệm, người ta điều chế được 40 cm3 khí hiđrô ở áp suất 750 mmHg và nhiệt độ 270C. Tính thể tích của lượng khí trên ở nhiệt độ 270C. Tính thể tích của lượng khí trên ở điều kiện chuẩn (áp suất 760mmHg và nhiệt độ 00C ).
Hướng dẫn giải
Trạng thái 1: p1 = 750 mmHg; T1 = 300 K; V1 = 40 cm3
Trạng thái 2: p0 = 760 mmHg; T0 = 273 K; V0 = ? cm3
Phương trình trạng thái khí lí tưởng: \(\frac{{{p_0}{V_0}}}{{{T_0}}} = \frac{{{p_1}{V_1}}}{{{T_1}}}\)
⇒ V0 = \(\frac{{{p_1}{V_1}{T_0}}}{{{p_0}{T_1}}} = \frac{{750.40.273}}{{760.300}}\)= 36 cm3
Vậy, thể tích khí ở điều kiện tiêu chuẩn là: V0 = 36 cm3
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Một lượng khí ở trong một xilanh thẳng đứng có pit-tông ở bên trong. Khí có thể tích 3ℓ ở 27oC. Biết diên tích tiết diện pit-tông S = 150 cm3, không có má sát giữa pit-tông và xilanh, pit-tông vẫn ở trong xilanh và trong quá trình áp suất không đổi. Khi đun nóng xilanh đến 100oC thì pit-tông được nâng lên một đoạn là bao nhiêu?
Câu 2: Hai bình có thể tích lần lượt là V1 = 40 ℓ, V2 = 10 ℓ thông nhau qua một cái van. Van chỉ mở khi áp suất trong bình 1 lớn hơn trong bình 2 từ 105Pa trở lên. Ban đầu bình 1 chứa khí ở áp suất p0 = 0,9.105 Pa và nhiệt độ T0 = 300 K, còn bình 2 là chân không. Người ta làm nóng đều cả hai bình từ nhiệt độ T0 lên nhiệt độ T = 500 K. Tính áp suất cuối cùng trong mỗi bình. bao nhiêu?
Câu 3: Một ống thuỷ tinh hình trụ (có tiết diện không đổi), một đầu kín được dùng làm ống Tô-ri-xen-li để đo áp suất khí quyển. Vì có một ít không khí ở trong ống trên mức thuỷ ngân, nên khi áp suất khí quyển là p0 (đo bằng ống Tô-ri-xen-li chuẩn) ở nhiệt độ T0 thì chiều cao cột thuỷ ngân H0 . Nếu ở nhiệt độ T1 chiều cao cột thuỷ ngân là H1 thì áp suất khí quyển pk là bao nhiêu? Biết chiều dài của ống từ mật thuỷ ngân trong chậu đến đầu trên được giữ không đổi và bằng L.
Câu 4: Một nhiệt kế khí gồm có hai bình giống nhau, dung tích mỗi bình là V, nối với nhau bởi một ống nằm ngang có chiều dài ℓ và tiết diện S. Trong ống có một giọt thuỷ ngân để ngăn cách không khí trong hai ống và để làm vật chuẩn chỉ nhiệt độ. Bình bên phải đặt trong máy điều nhiệt và được giữ ở nhiệt độ T0 . Tìm công thức cho sự phụ thuộc của nhiệt độ T của bình bên trái vào độ dời x của giọt thuỷ ngân. Cho V, ℓ, S là các giá trị hợp lí và suy ra rằng nhiệt kế này khá nhạy.
Câu 5: Một bình chứa 4,8 lít khí hiđrô ở 5.105 Pa ở 14 °C. Người ta tăng nhiệt độ của khí lên tới 26 °C. Vì bình không thật kín nên có một phần khí thoát ra ngoài và áp suất trong bình không thay đổi. Biết khối lượng mol của hiđrô là μ = 2.10-3 kg/mol. Khối lượng khí thoát ra ngoài là bao nhiêu?
3.2. Bài tập trắc nghiệm
Câu 1: Một bình chứa kín một chất khí ở nhiệt độ 57°C và áp suất 30atm. Người ta cho 2/3 lượng khí thoát ra khỏi bình và hạ nhiệt độ xuống còn 41°C. Tính áp suất của khí còn lại trong bình. Coi thể tích của bình chứa không thay đổi khi hạ nhiệt độ. Chọn đáp án đúng.
A. 6,98 atm
B. 10,1 atm
C. 7,66 atm
D. 5,96 atm
Câu 2: Hai bình có thể tích V1 = 40 lít, V2 = 10 lít thông với nhau bằng một ống có khóa ban đầu đóng. Khóa này chỉ mở nếu p1 ≥ p2 +105 Pa; p1, p2 là áp suất khí trong hai bình. Ban đầu bình 1 chứa khí ở áp suất p0 = 0,9.105 Pa và nhiệt độ T0 = 300K. Trong bình 2 là chân không. Người ta nung nóng đều hai bình từ T0 đến T = 500K. Tới nhiệt độ nào thì khóa mở? Tính áp suất cuối cùng trong bình 2?. Chọn đáp án đúng.
A. Tm = 393 K, p = 0,9.105 Pa.
B. Tm = 593 K, p = 0,9.105 Pa
C. Tm = 333 K, p = 0,4.105 Pa
D. Tm = 383 K, p = 0,6.105 Pa.
Câu 3: Một bình chứa khí hyđrô nén, thể tích 10 lít, nhiệt độ 7°C, áp suất 50 atm. Khi nung nóng bình, vì bình hở nên một phần khí thoát ra ngoài; phần khí còn lại có nhiệt độ 17°C còn áp suất vẫn như cũ. Tính khối lượng hyđrô đã thoát ra ngoài.
A. 1,89g
B. 2,32g
C. 4,78g
D. 1,47g
Câu 4: Người ta bơm khí ôxi ở điều kiện chuẩn và một bình có thể tích 500 lít. Sau nửa giờ bình chứa đầy khí ở nhiệt độ 24°C và áp suất 765 mmHg. Xác định khối lượng khí bơm vào sau mỗi giây. Coi quá trình bơm diễn ra 1 cách đều đặn, khối lượng riêng của không khí ở điều kiện tiêu chuẩn là ρ = 1,29 kg/m3.
A. 3,3 mg
B. 1,29 kg
C. 3,3 kg
D. 1,29 mg
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Phương trình trạng thái của khí lí tưởng Vật lý 10 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài giảng Phương trình trạng thái của khí lí tưởng này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :
-
Nêu được định nghĩa quá trình đẳng áp, viết được biểu thức liên hệ giữa thể tích và nhiệt độ tuyệt đối trong quá trình đẳng áp và nhận được dạng đường đẳng áp trong hệ tọa độ (p, T) và (p, t).
-
Hiểu được ý nghĩa vật lí của “Không độ tuyệt đối”.

