Lý 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số và Phương pháp Fre-nen
Trong các bài học trước, eLib đã cùng các em tìm hiểu các loại dao động. Ở bài học này, eLib xin giới thiệu đến các bạn cách tổng hợp dao động điều hòa cùng phương cùng tần số. Hi vọng đây sẽ là bài học bổ ích giúp các em học sinh có thể nắm chắc được kiến thức cũng như vận dụng vào làm bài tập.
Mục lục nội dung

1. Tóm tắt lý thuyết
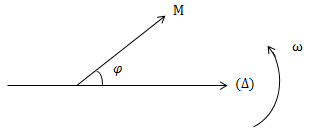
1.1. Vectơ quay
- Ta có thể biểu diễn một dao động x = Acos(ωt + φ) bằng một vectơ quay tại thời điểm ban đầu có các đặc điểm sau:
- Có góc tai góc tọa độ của Ox
- Có độ dài bằng biên độ dao động; OM = A
- Hợp với Ox một góc φ
1.2. Phương pháp giản đồ Fre-nen
a. Đặt vấn đề
Tìm tổng của hai dao động
x1 = A1cos(ωt + φ1), x2 = A2cos(ωt + φ2)
b. Phương pháp giản đồ Fre-nen
- Ta lần lượt ta vẽ hai vec tơ quay đặt trưng cho hai dao động:
- Ta thấy \(\overrightarrow {O{M_1}} \) và \(\overrightarrow {O{M_2}} \) quay với tốc độ góc ω thì \(\overrightarrow {OM} \) cũng quay với tốc độ góc là ω.
- Phương trình tổng hợp
- x = Acos(ωt+φ)
- Kết luận: Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số là một dao động điều hòa cùng phương, cùng tần số với hai dao động đó. Trong đó:
- \(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos ({\varphi _2} - {\varphi _1})} \) (1)
- \(\tan \varphi = \frac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}{\rm{cos}}{\varphi _1} + {A_2}\cos {\varphi _2}}}\) (2)
c. Ảnh hưởng của độ lệch pha
- Ta có:
- Δφ = φ2 – φ1 = k2π: x1, x2 cùng pha ⇒ A = A1 + A2 và φ = φ1 = φ2
- Δφ = φ2 – φ1 = (2k+1)π: x1, x2 ngược pha \(\left\{ \begin{array}{l} A = \left| {{A_1} - {A_2}} \right|\\ \varphi = {\varphi _1}neu{A_1} > {A_2} \end{array} \right.\)
- Δφ = (2k+1) \(\frac{\pi }{2}\) ⇒ x1 ⊥ x2 ⇒ A = \(\sqrt {A_1^2 + A_2^2} \)
2. Bài tập minh họa
2.1. Dạng 1: Tìm phương trình dao động tổng hợp
Tổng hợp các dao động sau: x1 = 2cos(2πt − π) cm và x2 = 3cos(2πt + π) cm
Hướng dẫn giải
Δφ = π − (−π) = 2π: x1, x2 cùng pha
⇒ A = A1 + A2 = 2 + 3 = 5 cm
φ = π; φ = −π
→ x = 5cos(2πt ± π) cm
2.2. Dạng 2: Tìm phương trình dao động thành phần
Cho 2 dao động cùng phương, cùng tần số có phương trình
Dao động tổng hợp x = x1 + x2 = \(6\sqrt 3 \cos (\omega t + \varphi )\). Tìm giá trị lớn nhất của A2 khi thay đổi A1?
Hướng dẫn giải
Định lý sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
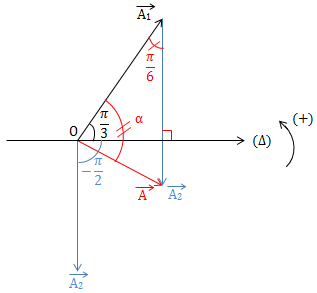
x = x1 + x2 ⇒ \(\overrightarrow A = \overrightarrow {{A_1}} + \overrightarrow {{A_2}} \)
\({A_2} = \frac{{6\sqrt 3 }}{{\frac{1}{2}}}.\sin \alpha = 12\sqrt 3 .\sin \alpha \)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương cùng tần số có các phương trình là: x1 = 4cos(10t + \(\frac{\pi }{4}\) cm và x2 = 3cos(10t + \(\frac{{3\pi }}{4}\)) cm. Xác định vận tốc cực đại và gia tốc cực đại của vật.
Câu 2: Dao động tổng hợp của hai dao động điều hòa cùng phương có biểu thức x = 5cos(6\(\pi \)t + \(\frac{\pi }{2}\)) cm. Dao động thứ nhất có biểu thức là x1 = 5cos(6\(\pi \)t + \(\frac{\pi }{3}\)) (cm). Tìm biểu thức của dao động thứ hai.
Câu 3: Một vật khối lượng m = 100g thực hiện đồng thời 2 dao động điều hòa cùng phương : \({x_1} = 5\cos (20t)\) cm, \({x_1} = 12\cos (20t + \pi )\) cm. Năng lượng dao động của vật là bao nhiêu?
Câu 4: Một vật thực hiện đồng thời 2 dao động điều hòa cùng phương, cùng tần số 10Hz và có biên độ lần lượt là 7cm và 8cm. Hiệu số pha của 2 dao động là p/3 rad. Độ lớn vận tốc của vật khi vật có li độ 12cm là bao nhiêu?
3.2. Bài tập trắc nghiệm
Câu 1: Cho 2 dao động điều hòa: x1 = 5cos(2πt +\(\frac{\pi }{4}\)) cm, x2 = 5cos(2πt + \(\frac{{3\pi }}{4}\)) cm. Tìm phương trình dao động tổng hợp.
A. x = 5\(\sqrt 2 \)cos(2πt + \(\frac{\pi }{2}\)) cm
B. x = 5\(\sqrt 2 \)cos(2πt) cm
C. x = 5\(\sqrt 2 \)cos(2πt − \(\frac{\pi }{2}\)) cm
D. x = 5\(\sqrt 2 \)cos(2πt +\(\frac{\pi }{6}\)) cm
Câu 2: Một vật tham gia đồng thời 2 dao động: x1 = 3cos(5πt+ \(\frac{\pi }{3}\)) cm, x2 = 3\(\sqrt 3 \)cos(5πt + \(\frac{\pi }{6}\)) cm. Tìm phương trình dao động tổng hợp.
A. x = 7,9cos(5πt + \(\frac{{41\pi }}{{180}}\)) cm
B. x = 7,9cos(πt + \(\frac{{41\pi }}{{180}}\)) cm
C. x = 7,9cos(5πt − \(\frac{{41\pi }}{{180}}\)) cm
D. x = 7,9cos(πt − \(\frac{{41\pi }}{{180}}\)) cm
Câu 3: Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là \({x_1} = 4\cos (10t + \frac{\pi }{4})\) cm và \({x_1} = 3\cos (10t - \frac{{3\pi }}{4})\) cm. Độ lớn vận tốc của vật ở vị trí cân bằng là:
A. 100 cm/s B. 50 cm/s C. 80 cm/s D. 10 cm/s
Câu 4: Vật khối lượng 400 g tham gia đồng thời 2 dao động điều hòa cùng phương với các phương trình: x1 = 3sin(5πt + \(\frac{\pi }{2}\)) cm, x2 = 6cos(5πt + \(\frac{\pi }{6}\)) cm. Vận tốc cực đại của vật là:
A. 81 cm/s
B. 81,7 cm/s
C. 81,7 m/s
D. 81 m/s
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Tổng hợp hai dao động điều hòa cùng phương, cùng tần số và Phương pháp Fre-nen Vật lý 12 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài giảng Tổng hợp hai dao động điều hòa và Phương pháp Fre-Nen này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như:
- Biểu diễn được phương trình dao động điều hòa bằng phương pháp vectơ quay.
- Vận dụng được phương pháp giản đồ Fre – nen để tìm phương trình dao động tổng hợp hai dao động điều hòa cùng phương, cùng tần số.
.png)
