Giải bài tập SBT Vật lý 11 Bài tập cuối chương IV: Từ trường
Hướng dẫn Giải bài tập SBT Vật lý 11 Bài 10 dưới đây sẽ giúp các em học sinh nắm vững phương pháp giải Bài tập cuối chương IV: Từ trường và ôn tập một số kiến thức trọng tâm. Mời các em cùng theo dõi.
Mục lục nội dung

1. Giải bài IV.1 trang 54 SBT Vật lý 11
Một đoạn dây dẫn thẳng dài 100 cm có dòng điện cường độ 20 A chạy qua và được đặt vuông góc với các đường sức từ trong một từ trường đều. Khi đó đoạn dây dẫn này bị tác dụng một lực từ 1,2 N. Xác định cảm ứng từ của từ trường đều.
A. 80T B. 60.10-3T
C. 70T D. 7,8.10-3T
Phương pháp giải
Áp dụng công thức:
B=F/I.l để tính cảm ứng từ
Hướng dẫn giải
- Vì dòng điện I hướng vuông góc với cảm ứng từ \(\vec B\), nên α = π/2 và sinα=1. Từ đó ta suy ra cảm ứng từ của từ trường đều có độ lớn bằng :
\(B = \frac{F}{{I\ell }} = \frac{{1,2}}{{{{20.100.10}^{ - 2}}}} = {60.10^{ - 3}}T\)
- Chọn đáp án: B
2. Giải bài IV.2 trang 54 SBT Vật lý 11
Một đoạn dây dẫn thẳng dài 1,8 m được đặt trong một từ trường đều có cảm ứng từ 0,80 T. Khi có dòng điện cường độ 4,0 A chạy qua đoạn dâ dãn này thì đoạn dây dẫn bị tác dụng một lực từ bằng 1,5 N. Góc hợp bởi hướng của dòng điện thẳng và hướng của từ trường là
A. 300 B. 450
C. 600 D .150
Phương pháp giải
Tính góc hợp bởi hướng của dòng điện thẳng và hướng của từ trường theo công thức:
\(\sin \alpha = \frac{F}{{BI\ell }}\)
Hướng dẫn giải
- Áp dụng công thức về lực từ: F=BIlsinα
- Ta suy ra góc hợp bởi hướng của dòng điện thẳng và hướng của từ trường:
\(\begin{array}{l} \sin \alpha = \frac{F}{{BI\ell }}\\ = \frac{{1,5}}{{0,80.4,0.1,8}} = 0,26\\ \Rightarrow \alpha = {15^0} \end{array}\)
- Chọn đáp án: D
3. Giải bài IV.3 trang 54 SBT Vật lý 11
Một đoạn dây dẫn dài 0,80 m đặt nghiêng một góc 600 so với hướng của các đường sức từ trong một từ trường đều có cảm ứng từ 0,50 T. Khi dòn điện chạy qua đoạn dây dẫn này có cường độ 7,5 A, thì đoạn dây dẫn bị tác dụng một lực từ bằng
A. 4,2 N.
B. 2,6 N.
C. 3,6 N.
D. 1,5N.
Phương pháp giải
Áp dụng công thức:
\(F = BIlsin\alpha \) để tính lực từ
Hướng dẫn giải
- Lực từ tác dụng là:
\(\begin{array}{l} F = BIlsin{60^0}\\ \approx {0,50.7,5.0,8.10^{ - 2}}.0,87 \approx 2,6N \end{array}\)
- Chọn đáp án B
4. Giải bài IV.4 trang 55 SBT Vật lý 11
Khi cho dòng điện cường độ 10 A chạy qua một vòng dây dẫn đặt trong không khí, thì cảm ứng từ tại tâm của vòng dây dẫn có độ lớn là 2,1.10-4T. Bán kính của vòng dây là
A. 5,0 cm.
B. 0,30 cm.
C. 3,0 cm.
D. 2,5 cm.
Phương pháp giải
Tính bán kính theo công thức:
\({R = 2\pi {{.10}^{ - 7}}\frac{I}{B}}\)
Hướng dẫn giải
- Ta có:
\(\begin{array}{*{20}{l}} {B = 2\pi {{.10}^{ - 7}}\frac{I}{R}}\\ { \Rightarrow R = 2\pi {{.10}^{ - 7}}\frac{I}{B}}\\ { = 2\pi {{.10}^{ - 7}}\frac{{10}}{{{{2,1.10}^{ - 4}}}} \approx 0,03m = 3cm} \end{array}\)
Vậy bán kính của vòng dây là: 3cm
- Chọn đáp án C
5. Giải bài IV.5 trang 55 SBT Vật lý 11
Một ống dây dẫn hình trụ dài 85 cm (không lõi sắt) gồm 750 vòng dây, trong đó có dòng điện cường độ 5,6 A. Cảm ứng từ bên trong ống dây dẫn là
A. 6,2T
B. 6,2.10−4T
C. 6,2.10−2T
D. 6,2.10−3T
Phương pháp giải
Áp dụng công thức:
\(B = 4\pi {.10^{ - 7}}\frac{{NI}}{l}\) để tính cảm ứng từ
Hướng dẫn giải
- Cảm ứng từ bên trong ống dây dẫn:
\(\begin{array}{l} B = 4\pi {.10^{ - 7}}\frac{{NI}}{l}\\ = {4.3,14.10^{ - 7}}.\frac{{750}}{{{{85.10}^{ - 2}}}}.5,6 = {6,2.10^{ - 3}}T \end{array}\)
- Chọn đáp án D
6. Giải bài IV.6 trang 55 SBT Vật lý 11
Bắn một prôtôn với vận tốc 1,5.105m/sm/s bay vào một từ trường đều theo hướng vuông góc với các đường sức từ. Cảm ứng từ của từ trường là 2,0.10−4T. Prôtôn có điện tích 1,6.10-19 C và khối lượng 1,672.10-27 kg. Bán kính quỹ đạo của prôtôn là:
A. 0,784 m.
B. 7,84 m.
C. 0,784 cm.
D. 7,84 cm.
Phương pháp giải
Áp dụng công thức:
\(R = \frac{{mv}}{{|q|B}}\) để tính bán kính quỹ đạo
Hướng dẫn giải
- Bán kính quỹ đạo của prôtn là:
\(\begin{array}{l} R = \frac{{mv}}{{|q|B}}\\ \frac{{{{1,672.10}^{ - 27}}{{.1,5.10}^5}}}{{{{2.10}^{ - 4}}{{.1,6.10}^{ - 19}}}} = 7,84m \end{array}\)
- Chọn đáp án B.
7. Giải bài IV.7 trang 55 SBT Vật lý 11
Cho hai dòng điện có cùng cường độ 8 A chạy trong hai dây dẫn thẳng dài, đặt vuông góc với nhau, cách nhau một khoảng 8,0 cm trong chân không: dây dẫn thứ nhất thẳng đứng có dòng điện chạy từ dưới lên trên, dây dẫn thứ hai thẳng ngang có dòng điện chạy từ trái qua phải. Xác định cảm ứng từ tại trung điểm của khoảng cách giữa hai dây dẫn này.
Phương pháp giải
- Vận dụng quy tắc nắm tay phải để xác định chiều vecto cảm ứng từ
- Tính độ lớn cảm ứng từ theo công thức:
\({R = 2\pi {{.10}^{ - 7}}\frac{I}{B}}\)
- Độ lớn cảm ứng từ tổng hợp được tính theo công thức:
\(B = {B_1}\sqrt 2 \)
Hướng dẫn giải
Khoảng cách giữa hai dây dẫn thẳng có dòng điện I1 và I2 là đoạn thẳng CD = d = 8,0 cm nằm trong cùng mặt phẳng ngang p chứa dòng điện I2.
Hai vectơ cảm ứng từ \(\vec B_1\) và \(\vec B_2\) lần lượt do I1 và I2 gây ra tại trung điểm M của đoạn CD có hướng như trên Hình IV. 1G:
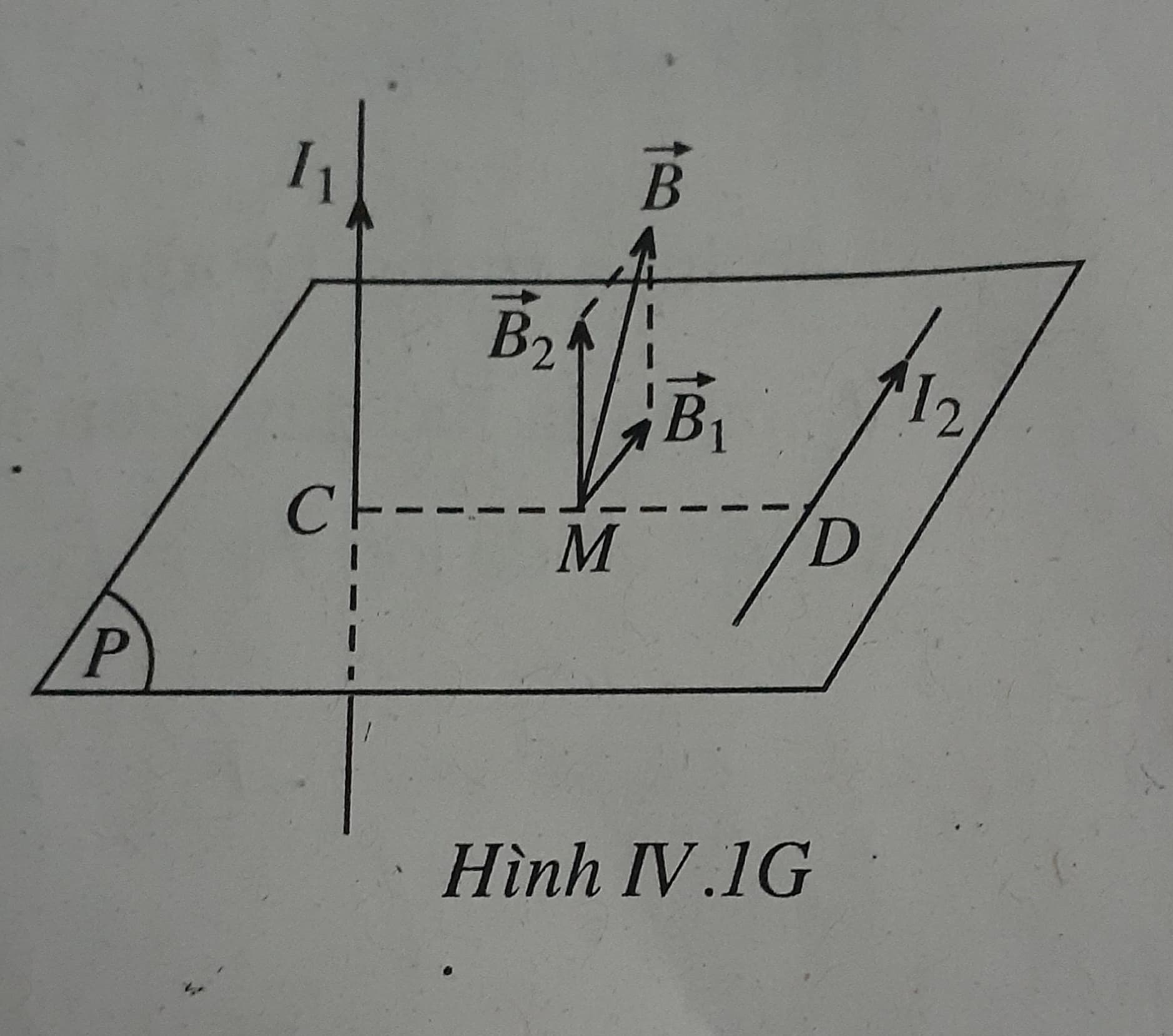
−\(\vec B_1\) song song với dây dẫn có dòng điện I2 và cùng chiều với I2, \(\vec B_2\) song song với dây dẫn có dòng điện I1 và cùng chiều với I1, có độ lớn bằng nhau
\({B_1} = {B_2} = {2.10^{ - 7}}.\frac{{8,0}}{{{{4,0.10}^{ - 2}}}} = {4,0.10^{ - 5}}T\)
- Vecto cảm ứng từ tổng hợp tại điểm M:
\(\vec B = \vec B_1 + \vec B_2\)
- Vì tính chất vuông góc nên cảm ứng từ là:
\(B = {B_1}\sqrt 2 = 4\sqrt 2 {.10^{ - 5}}T\)
8. Giải bài IV.8 trang 55 SBT Vật lý 11
Ba dòng điện có cùng cường độ \({I_1} = {I_2} = {I_3} = I\) và cùng chiều chạy trong ba dây dẫn thẳng dài, đồng phẳng, song song cách đều nhau.
a) Xác định lực từ tác dụng lên một đơn vị dài của dây dẫn có dòng điện I2 nằm giữa I1 và I3.
b) Nếu đổi chiều dòng điện I2 thì lực từ tác dụng lên nó thay đổi thế nào?
Phương pháp giải
a) Vận dụng quy tắc bàn tay phải để xác định chiều của cảm ứng từ
Tính lực từ theo công thức:
\({F_0} = \frac{F}{\ell } = B{I_2} \) với \({B_1} = {B_2} = {2.10^{ - 7}}.\frac{I}{a}\)
b) Khi đổi chiều dòng điện thì lực từ vẫn không đổi trong trường hợp này
Hướng dẫn giải
Áp dụng quy tắc bàn tay phải, ta xác định được các vectơ cảm ứng từ B1 và B3 do hai dòng điện I1và I3 gây ra tại mọi điểm trên dây dẫn có dòng điện I2 nằm giữa I1 và I3 đều có phương vuông góc vớimặt phẳng chứa ba dòng điện, có chiều ngược nhau (Hình IV.3G) và có cùng độ lớn:
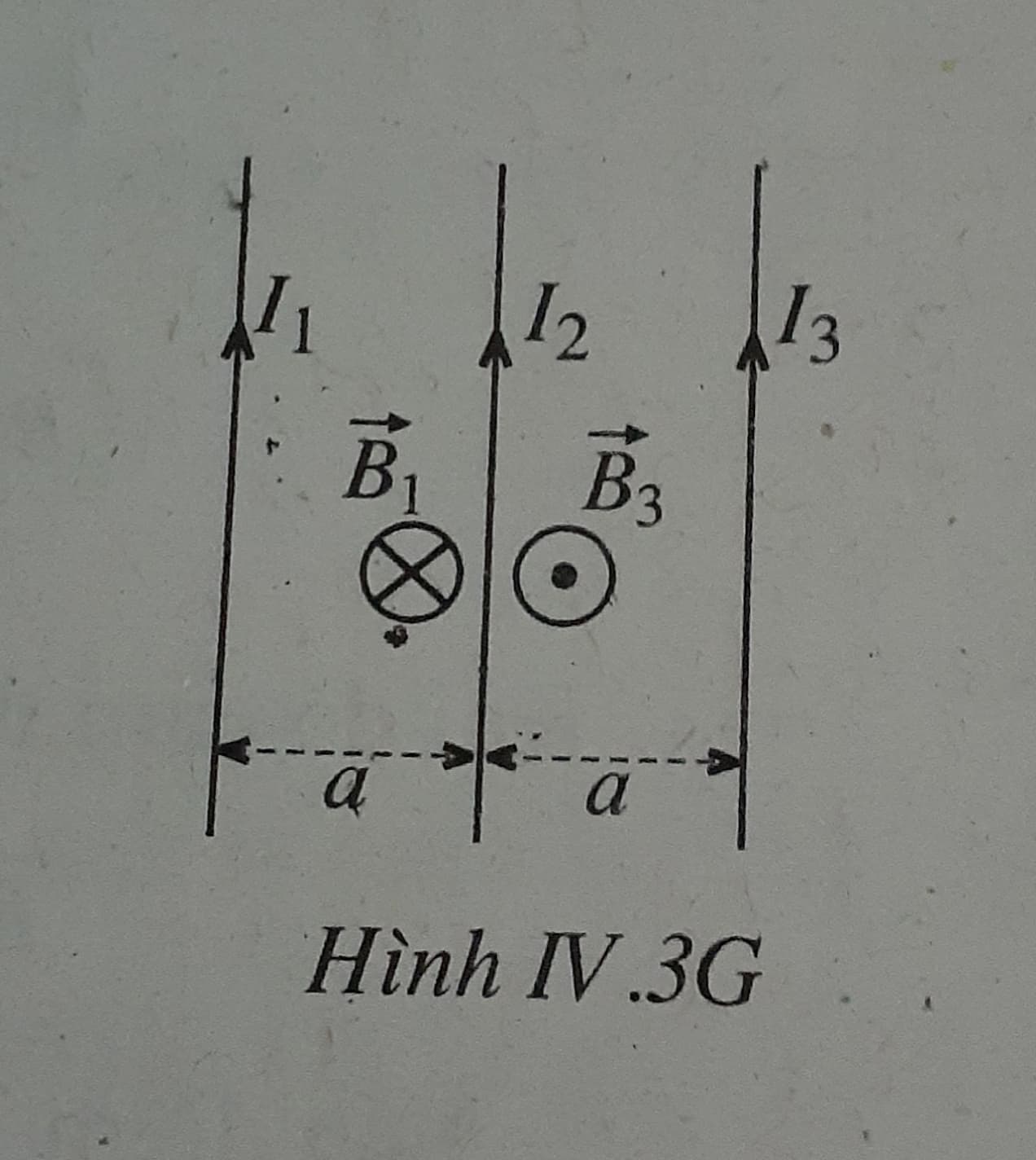
\({B_1} = {B_2} = {2.10^{ - 7}}.\frac{I}{a}\)
nên vectơ cảm ứng từ tổng hợp tại mọi điểm trên dây dẫn có dòng điện I2 luôn có giá trị bằng không:
\(\vec B = \overrightarrow {{B_1}} + \overrightarrow {{B_3}} = \vec 0\)
- Do đó, lực từ tác dụng lên mỗi đơn vị dài trên dây dẫn có dòng điện I2 cũng luôn có giá trị bằng không:
\({F_0} = \frac{F}{\ell } = B{I_2} = 0\)
b) Nếu đổi chiều dòng điện I2 thì lực từ tác dụng lên I2 vẫn bằng không.
