Giải bài tập SBT Vật lý 11 Bài tập cuối chương V: Cảm ứng điện từ
eLib xin giới thiệu đến các em học sinh nội dung Hướng dẫn giải Bài tập cuối chương V: Cảm ứng điện từ dưới đây, nhằm giúp các em nắm vững cách giải các bài tập chi tiết và rõ ràng. Hy vọng đây sẽ là tài liệu tham khảo hữu ích với các em học sinh.
Mục lục nội dung
1. Giải bài V.1 trang 66 SBT Vật lý 11
2. Giải bài V.2 trang 66 SBT Vật lý 11
3. Giải bài V.3 trang 66 SBT Vật lý 11
4. Giải bài V.4 trang 66 SBT Vật lý 11
5. Giải bài V.5 trang 66 SBT Vật lý 11
6. Giải bài V.6 trang 67 SBT Vật lý 11
7. Giải bài V.7 trang 67 SBT Vật lý 11
8. Giải bài V.8 trang 67 SBT Vật lý 11

1. Giải bài V.1 trang 66 SBT Vật lý 11
Một ống dây dẫn hình trụ gồm nhiều vòng dây đồng quấn sít nhau trên suốt chiều dài của nó. Dây đồng có đường kính 0,50 mm. Dòng điện chạy trong các vòng dây có cường độ 2,0 A. Xác định độ lớn của cảm ứng từ trong lòng ống dây dẫn này.
A. 5,0 mT. B. 4,2 mT.
C. 2,5 T. D. 3,5 mT.
Phương pháp giải
Áp dụng công thức:
\(B = 4\pi {.10^{ - 7}}.\frac{1}{d}I\) để tính cảm ứng từ trong ống dây dẫn
Hướng dẫn giải
- Cảm ứng từ trong ống dây dẫn hình trụ có độ dài l, gồm N vòng dây trong đó có dòng điện cường độ I được tính theo công thức:
\(B = 4\pi {.10^{ - 7}}N\frac{I}{l}\)
- Vì N vòng dây dẫn có cùng đường kính d được quấn sít nhau trên suốt chiều dài l của ống dây, nên ta có: l = Nd. Thay vào trên, ta tìm được :
\(\begin{array}{l} B = 4\pi {.10^{ - 7}}.\frac{1}{d}I\\ = {4.3,14.10^{ - 7}}.\frac{1}{{{{0,50.10}^{ - 3}}}}.2,0 \approx 5,0mT \end{array}\)
- Chọn đáp án A
2. Giải bài V.2 trang 66 SBT Vật lý 11
Một khung dây dẫn phẳng có diện tích 28 cm2 được đặt trong từ trường đều có cảm ứng từ 1,5.10-4 T. Xác định từ thông qua khung dây dẫn khi t trường hợp với mặt khung dây một góc 300.
A. 5,4.10-7 Wb. B. 2,1.10-7 Wb.
C. 3,6.10-5 Wb D. 8,3.10-6 Wb.
Phương pháp giải
Tính từ thông theo công thức:
\({\rm{\Phi }} = Bscos\alpha \)
Hướng dẫn giải
- Từ thông qua khung dây dẫn là:
\(\begin{array}{l} {\rm{\Phi }} = Bscos\alpha \\ = {1,5.10^{ - 4}}{.28.10^{ - 4}}.0,5 = {2,1.10^{ - 7}}Wb \end{array}\)
- Chọn đáp án B
3. Giải bài V.3 trang 66 SBT Vật lý 11
Một thanh kim loại chuyển động với vận tốc 25 m/s trong một từ trường đều có cảm ứng từ 3,8 mT theo phương vuông góc với các đường sức từ. Ở hai đầu của nó có một hiệu điện thế 28 mV. Độ dài của thanh kim loại là
A. 19cm
B. 42 cm.
C.32 cm.
D. 29 cm.
Phương pháp giải
Dựa vào công thức tính từ thông và công thức Fa-ra-đây, tính được độ dài của thanh kim loại theo công thức: \(\ell = \frac{u}{{Bv}}\)
Hướng dẫn giải
- Sau khoảng thời gian Δt, thanh kim loại có độ dài l chuyển động với vận tốc \(\vec v\) theo phương vuông góc với từ trường đều \(\vec B\), quét được diện tích ΔS = IvΔt. Khi đó từ thông qua diện tích quét ΔS bằng :
\({\rm{\Delta \Phi }} = B{\rm{\Delta }}S = B\ell v{\rm{\Delta }}t\)
- Áp dụng công thức của định luật Fa-ra-đây, ta có :
\(\left| {{e_c}} \right| = |\frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}| = B\ell v\)
- Vì thanh kim loại có hai đầu hở, nên suất điện động cảm ứng xuất hiện trong thanh này bằng hiệu điện thế giữa hai đầu của nó : |ec| = u = 28 mV. Thay vào công thức trên, ta xác định được độ dài của thanh kim loại :
\(\ell = \frac{u}{{Bv}} = \frac{{{{28.10}^{ - 3}}}}{{{{3,8.10}^{ - 3}}.25}} = 29cm\)
- Chọn đáp án D
4. Giải bài V.4 trang 66 SBT Vật lý 11
Một thanh kim loại dài 1,2 m chuyển động với vận tốc 15 m/s trong từ trường đều theo hướng hợp với các đường sức từ một góc 30°. Xác định độ lớn của cảm ứng từ nếu trong thanh này xuất hiện suất điện động cảm ứng 6,2 mV.
A. 0,69 mT.
B. 2,4 mT.
C. 0,20 mT.
D. 3,2 mT.
Phương pháp giải
- Tính suất điện động cảm ứng theo công thức:
\(\left| {{e_c}} \right| = |\frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}| = B\ell v\sin {30^o}\)
- Độ lớn của cảm ứng từ được tính theo công thức:
\(B = \frac{{\left| {{e_c}} \right|}}{{\ell v\sin {{30}^0}}} \)
Hướng dẫn giải
- Sau khoảng thời gian Δt, thanh kim loại có độ dài l chuyển động với vận tốc \(\vec v\) theo phương hợp với từ trường đều \(\vec B\) một góc α, nên diện tích quét vuông góc với các đường sức từ sẽ là ΔS = lvsinα.Δt, do đó từ thông qua diện tích quét ΔS bằng :
\({\rm{\Delta \Phi }} = B{\rm{\Delta }}S = B\ell v\sin \alpha .{\rm{\Delta }}t\)
- Áp dụng công thức của định luật Fa-ra-đây, ta có :
\(\left| {{e_c}} \right| = |\frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}| = B\ell v\sin {30^o}\)
- Từ đó suy ra:
\(B = \frac{{\left| {{e_c}} \right|}}{{\ell v\sin {{30}^0}}} = \frac{{{{6,2.10}^{ - 3}}}}{{1,2.15.0,50}} \approx 0,69mT\)
- Chọn đáp án A
5. Giải bài V.5 trang 66 SBT Vật lý 11
Một thanh đồng dài 20 cm, quay với tốc độ 50 vòng/s trong một từ trường đều có cảm ứng từ 25 mT quanh một trục song song với từ trường và đi qua một đầu và vuông góc với thanh đồng. Suất điện động cảm ứng xuất hiện trong thanh đồng là
A. 0,60 V.
B. 0,157 V.
C. 2,5 V.
D. 36 V.
Phương pháp giải
- Tính từ thông theo công thức:
\({\rm{\Delta \Phi }} = B{\rm{\Delta }}S = B\pi {\ell ^2}.n{\rm{\Delta }}t\) với \(\Delta S = \pi {l^2}n\Delta t\)
- Áp dụng công thức:
\(|{e_c}| = B\pi .{l^2}.n\) để tính suất điện động cảm ứng
Hướng dẫn giải
- Sau khoảng thời gian Δt, thanh đồng quay quanh một trục song song với từ trường và đi qua một đầu của nó, quét được một diện tích :
\(\Delta S = \pi {l^2}n\Delta t\)
với l là độ dài và n là tốc độ quay của thanh đồng. Khi đó từ thông qua diện tích quét ΔS có trị số bằng :
\({\rm{\Delta \Phi }} = B{\rm{\Delta }}S = B\pi {\ell ^2}.n{\rm{\Delta }}t\)
- Áp dụng công thức của định luật Fa – ra – đây \(\left| {{e_c}} \right| = |\frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}|\) ta xác định được suất điện động cảm ứng trong thanh kim loại:
\(\begin{array}{l} |{e_c}| = B\pi .{l^2}.n\\ = {25.10^{ - 3}}.3,14.{({20.10^{ - 2}})^2}.50 = 0,157V \end{array}\)
- Chọn đáp án B
6. Giải bài V.6 trang 67 SBT Vật lý 11
Một vòng dây dẫn diện tích 100 cm2 được đặt trong một từ trường đều có cảm ứng từ 1,0 T sao cho mặt phẳng vòng dây vuông góc với các đường sức từ. Suất điện động cảm ứng xuất hiện trong vòng dây dẫn khi cắt bỏ từ trường trong khoảng thời gian 10ms là
A. 0,60 V.
B. 5,0 mV.
C. 1,0 V
D. 10 mV
Phương pháp giải
- Áp dụng công thức:
\(\left| {{\rm{\Delta \Phi }}} \right| = \left| {0 - BS} \right| = BS\) để tính từ thông
- Tính suất điện động cảm ứng theo công thức:
\(\left| {{e_c}} \right| = \frac{{BS}}{{{\rm{\Delta }}t}}\)
Hướng dẫn giải
- Trong khoảng thời gian Δt cắt bỏ từ trường, từ thông qua vòng dây dẫn biến thiên một lượng:
\(\left| {{\rm{\Delta \Phi }}} \right| = \left| {0 - BS} \right| = BS\)
- Áp dụng công thức của định luật Fa-ra-đây:
\({e_c} = |\frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}|\)
- Ta xác định được suất điện động cảm ứng xuất hiện trong vòng dây dẫn:
\(\left| {{e_c}} \right| = \frac{{BS}}{{{\rm{\Delta }}t}} = \frac{{{{1,0.100.10}^{ - 4}}}}{{{{10.10}^{ - 3}}}} = 1,0V\)
- Chọn đáp án C
7. Giải bài V.7 trang 67 SBT Vật lý 11
Một đĩa tròn A bằng đồng, bán kính 5,0cm, đặt trong từ trường đều có cảm ứng từ 0,20 T sao cho trục quay của đĩa này song song với các đường sức từ (Hình V.l). Khi cho đĩa A quay đều với tốc độ 3,0 vòng/s quanh trục của nó, thì có một dòng điện chạy trong mạch kín abGa (với a, b là hai tiếp điểm trượt) qua điện kế G. Xác định :
a) Độ lớn của suất điện động xuất hiện trong mạch abGa.
b) Chiều của dòng điện chạy trong mạch aba, nếu từ trường hướng từ ngoài vào mặt phẳng hình vẽ và đĩa A quay ngược chiều kim đồng hồ.
Phương pháp giải
- Tính từ thông theo công thức:
\({\rm{\Delta \Phi }} = B{\rm{\Delta }}S = B\pi {R^2}n{\rm{\Delta }}t\)
- Độ lớn của suất điện động được tính theo công thức:
\(\begin{array}{l} |{e_c}| = B\pi {R^2}n\\ \end{array}\)
Hướng dẫn giải
- Sau khoảng thời gian Δt, bán kính của đĩa tròn A nằm trùng với đoạn ab quét được một điện tích:
\(\Delta S = \pi {R^2}n\Delta t\)
- Khi đó từ thông qua diện tích quét ΔS biến thiên một lượng:
\({\rm{\Delta \Phi }} = B{\rm{\Delta }}S = B\pi {R^2}n{\rm{\Delta }}t\)
- Áp dụng công thức của định luật Fa-ra-đây:
\(\left| {{e_c}} \right| = |\frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}|\), ta xác định được suất điện động xuất hiện trong mạch là:
\(\begin{array}{l} |{e_c}| = B\pi {R^2}n\\ = 0,20.3,14.{({5,0.10^{ - 2}})^2}.3,0 \approx 4,7mV \end{array}\)
b) Vì từ thông qua diện tích quét ΔS của đĩa A luôn tăng (ΔΦ>0) theo thời gian quay, nên theo định luật Len-xơ, dòng điện cảm ứng iC chạy trong mạch aba phải theo chiều đi từ b qua đĩa A đến a sao cho từ trường cảm ứng của dòng ic luôn ngược chiều với từ trường \(\vec B\) , chống lại sự tăng của từ thông qua diện tích quét ΔS và có tác dụng cản trờ chuyển động của đĩa A.
8. Giải bài V.8 trang 67 SBT Vật lý 11
Một ống dây dẫn hình trụ dài 62,8 cm, gồm 1000 vòng dây quấn sít nhau, điện trở rất nhỏ và bên trong nó là không khí, tiết diện của mỗi vòng dây có diện tích 50cm2. Dòng điện trong ống dây dẫn có cường độ 4,0A. Xác định :
a) Độ lớn của cảm ứng từ trong lòng ống dây dẫn.
b) Từ thông qua ống dây dẫn.
c) Độ tự cảm của ống dây dẫn.
Phương pháp giải
a) Áp dụng công thức:
\(B = 4\pi {.10^{ - 7}}.N\frac{I}{l}\) để tính cảm ứng từ
b) Từ thông qua ống dây được tính theo công thức:
\(\begin{array}{l} {\rm{\Phi }} = NBS\\ \end{array}\)
c) Tính độ tự cảm theo công thức:
\(L = \frac{{\rm{\Phi }}}{I}\)
Hướng dẫn giải
a) Độ lớn của cảm ứng từ trong lòng ống dây dẫn:
\(\begin{array}{l} B = 4\pi {.10^{ - 7}}.N\frac{I}{l}\\ = {4.3,14.10^{ - 7}}.1000\frac{4}{{{{62,8.10}^{ - 2}}}} = {8,0.10^{ - 3}}T \end{array}\)
b) Từ thông qua ống dây dẫn gồm N vòng dây:
\(\begin{array}{l} {\rm{\Phi }} = NBS\\ = {1000.8,0.10^{ - 3}}{.50.10^{ - 4}} = {40.10^{ - 3}}{\rm{Wb}} \end{array}\)
c) Độ tự cảm của ống dây dẫn:
\(L = \frac{{\rm{\Phi }}}{I} = \frac{{{{40.10}^{ - 3}}}}{{4,0}} = 10mH\)
9. Giải bài V.9 trang 67 SBT Vật lý 11
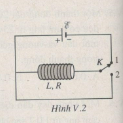
Một ống dây dẫn có độ tự cảm 200 mH và có điện trở 2,0Ω được mắc vào mạch điện chứa nguồn điện E(với r ≈ 0) và một khoá đảo mạch K (Hình V.2). Hỏi cường độ đòng điện trong mạch giảm bao nhiêu lần khi chuyển đảo mạch K từ tiếp điểm 1 sang tiếp điểm 2 trong khoảng thời gian 50ms để cắt nguồn điện khỏi mạch và nối đoản mạch ống dây dẫn ?
Phương pháp giải
- Tính cường độ dòng điện theo công thức:
I0=E/(R+r)
- Tính suất điện động tự cảm theo công thức:
\({e_{tc}} = - L\frac{{{\rm{\Delta }}i}}{{{\rm{\Delta }}t}}\)
- Lập tỉ số:
\({ - \frac{{\Delta i}}{i} = \frac{{R\Delta t}}{L} = - \frac{{I - {I_0}}}{I} = n - 1}\) để tìm độ giảm cường độ trong mạch
Hướng dẫn giải
- Khi khoá K đặt tại tiếp điểm 1: dòng điện trong ống dây dẫn có cường độ bằng:
I0=E/(R+r)
- Khi khoá K đặt tại tiếp điểm 2: dòng điện i trong ống dây có cường độ giảm từ I0 đến I, làm xuất hiện suất điện động tự cảm trong nó có trị số:
\({e_{tc}} = - L\frac{{{\rm{\Delta }}i}}{{{\rm{\Delta }}t}}\)
- Áp dụng định luật Ôm cho mạch điện gồm cuộn dây dẫn, (L, R) có suất điện động tự cảm etc bị nối đoản mạch, ta có etc=Ri
\(\begin{array}{l} \Rightarrow - L\frac{{{\rm{\Delta }}i}}{{{\rm{\Delta }}t}} = Ri\\ \Rightarrow - \frac{{{\rm{\Delta }}i}}{i} = \frac{{R{\rm{\Delta }}t}}{L} = \frac{{{{2,0.50.10}^{ - 3}}}}{{{{200.10}^{ - 3}}}} = 0,50 \end{array}\)
- Thay số:
\(\begin{array}{l} - \frac{{{\rm{\Delta }}i}}{i} = - \frac{{I - {I_0}}}{I} = n - 1\\ n - 1 = 0,50\\ = > n = 1 + 0,50 = 1,50 \end{array}\)
ta tìm được n = 1,5
10. Giải bài V.10 trang 68 SBT Vật lý 11
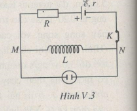
Một đèn nêon (Ne) được mắc vào mạch điện nhự Hình V.3, với nguồn điện E = 1,6V; r = 1,0 Ω ; điện trở R = 7,0 Ω và cuộn dây dẫn L = 10 mH.Đèn nêon trong mạch chỉ phát sáng (do hiện tượng phóng điện tự lực) khi hiệu điện thế giữa hai cực của nó đạt từ 80 V trở lên.
a) Khoá K đóng. Đèn nêon có phát sáng không ?
b) K đang đóng. Người ta đột nhiên mở khoá K và thấy đèn nêon loé sáng. Hỏi khoảng thời gian Δt để cường độ dòng điện trong mạch giảm đến không, phải thoả mãn điều kiện gì?
Phương pháp giải
a) Áp dụng công thức:
\({I_0} = \frac{E}{{R + r}} \) để tính cường độ dòng điện
b) Từ công thức Fa-ra-đây:
\({u_{tc}} \approx \left| {{e_{tc}}} \right| = L|\frac{{{\rm{\Delta }}i}}{{{\rm{\Delta }}t}}|\)
Tính thời gian Δt để cường độ dòng điện trong mạch giảm đến không theo công thức:
\({\rm{\Delta }}t \le \frac{{L\left| {I - {I_0}} \right|}}{{80}}\)
Hướng dẫn giải
a) Khi khóa K đang đóng: dòng điện trong mạch điện có cường độ không đổi xác định theo định luật Ôm cho toàn mạch:
\({I_0} = \frac{E}{{R + r}} = \frac{{1,6}}{{7,0 + 1,0}} = 0,20A\)
Hiệu điện thế giữa hai cực của đèn neon nhỏ không đáng kể, nên đèn không phát sáng.
b) Khi ngắt khóa K: cường độ dòng điện i trong cuộn cảm L giảm nhanh từ I0 = 0,20A đến I = ,0 làm xuất hiện trong nó suất điện động tự cảm etc và hình thành giữa hai đầu đoạn mạch MN một hiệu điện thế
\({u_{tc}} \approx \left| {{e_{tc}}} \right| = L|\frac{{{\rm{\Delta }}i}}{{{\rm{\Delta }}t}}|\)
(do cuộn cảm L có điện trở nhỏ không đáng kể)
- Muốn đèn lóe sáng thì utc ≥ 80V
\(\begin{array}{l} \Rightarrow L\left| {\frac{{{\rm{\Delta }}i}}{{{\rm{\Delta }}t}}} \right| \ge 80\\ \Rightarrow {\rm{\Delta }}t \le \frac{{L\left| {{\rm{\Delta }}i} \right|}}{{80}}\\ \Rightarrow {\rm{\Delta }}t \le \frac{{L\left| {I - {I_0}} \right|}}{{80}} \Rightarrow {\rm{\Delta }}t \le 25\mu s \end{array}\)