10 đề thi Học kì 1 môn Toán lớp 11 năm 2020 có đáp án
Nhằm giúp các em học sinh ôn tập và nắm vững các kiến thức đã học, eLib xin gửi đến các em bộ tài liệu 10 đề thi HK1 môn Toán 11 năm 2020 có đáp án. Tài liệu được biên soạn theo cấu trúc của các trường trên cả nước với đáp án và hướng dẫn giải chi tiết. Hi vọng đây sẽ là một tài liệu tham khảo hữu ích trong quá trình học tập của các em.
Mục lục nội dung

1. Đề thi học kì 1 môn Toán 11 số 1
TRƯỜNG THPT VÕ VĂN KIỆT
ĐỀ THI HK1
NĂM HỌC: 2020-2021
MÔN: TOÁN – LỚP 11
Thời gian: 60 phút (không kể thời gian giao đề)
Câu 1 (2,5 điểm). Giải các phương trình sau:
a) \(2cosx - \sqrt 3 = 0\)
b) \(si{n^2}x - 3sinxcosx + 2co{s^2}x = 0\)
c) \(\sqrt 2 si{n^3}\left( {x - \frac{\pi }{4}} \right) = 2sinx\)
Câu 2 ( 1,5 điểm).
a) Tìm hệ số x7 trong khai triển \({\left( {3x + 1} \right)^{11}}\) thành đa thức.
b) Tìm số tự nhiên n > 5 trong khai triển \({\left( {x + \frac{1}{3}} \right)^n}\) thành đa thức biến x có hệ số x7 bằng 9 lần hệ số x5.
Câu 3 ( 2,0 điểm). Một hộp có chứa 9 viên bi xanh được đánh số từ 1 đến 9 và 5 viên bi đỏ được đánh số từ 10 đến 14. Chọn ngẫu nhiên hai viên bi.
a) Tính xác suất để chọn được 2 viên bi cùng màu.
b) Tính xác suất để chọn được hai viên bi khác màu và tổng 2 số ghi trên hai viên bi là số lẻ.
Câu 4 ( 2,0 điểm). Trong mặt phẳng (Oxy) cho điểm A( -2;3) và đường tròn (C) có tâm I(3;-1) bán kính R = 4.
a) Tìm tọa độ điểm A’ là ảnh của điểm A qua phép tịnh tiến \({T_{\overrightarrow u }}\) với \(\overrightarrow u = \left( {4; - 1} \right)\).
b) Viết phương trình đường tròn ( C’) là ảnh của đường tròn ( C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng trục Oy và phép vị tự tâm O tỉ số k = -2.
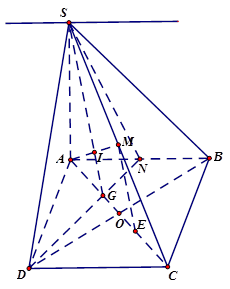
Câu 5 ( 2,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt trung điểm SC và AB.
a) Tìm giao tuyến \(\left( {SAC} \right) \cap \left( {SBD} \right)\;\) và \(\left( {SAB} \right) \cap \left( {SCD} \right).\)
b) Tìm giao điểm I của AM với mặt phẳng (SND) và tính \(\frac{{AI}}{{AM}}\).
-----------------HẾT---------------------
Học sinh không được sử dụng tài liệu. CBCT không giải thích gì thêm.
HƯỚNG DẪN CHẤM
|
Câu |
Đáp án |
Điểm |
|
1 (2,5 điểm) |
a) \(\begin{array}{l} 2cosx - \sqrt 3 = 0\\ \Leftrightarrow cosx = \frac{{\sqrt 3 }}{2}\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = \frac{\pi }{6} + k2\pi }\\ {x = \frac{{ - \pi }}{6} + k2\pi } \end{array}} \right.\;\left( {k\in Z} \right) \end{array}\) |
0.5
0.5 |
|
b) \(\cos x = 0\) không thỏa mãn phương trình. \(\cos x \ne 0\;\) phương trình trở thành \(\begin{array}{l} ta{n^2}x - 3tanx + 2 = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {tanx = 1}\\ {tanx = 2} \end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = \frac{\pi }{4} + k\pi }\\ {x = arctan2 + k\pi } \end{array}} \right.\;\left( {k\in Z} \right) \end{array}\) |
0.25
0.25 0.25 0.25 |
|
|
c) Đặt \(t = x - \frac{\pi }{4}\;\), phương trình trở thành \(\begin{array}{l} si{n^3}t = \sqrt 2 sin\left( {t + \frac{\pi }{4}} \right)\\ \Leftrightarrow si{n^3}t = sint + cost\;\;\; \end{array}\) sin t = 0 không thỏa mãn. \(\sin t \ne 0\) phương trình trở thành: \(\begin{array}{l} 1 = \frac{1}{{{{\sin }^2}t}} + \frac{{\cos t}}{{{{\sin }^3}t}}\\ \Leftrightarrow {\cot ^3}t + {\cot ^2}t + \cot t = 0\\ \Leftrightarrow \cot t = 0\\ \Leftrightarrow t = \frac{\pi }{2} + k\pi \\ \Rightarrow x = \frac{{3\pi }}{4} + k\pi \end{array}\) |
0.25
0.25 |
|
|
2 (1,5 điểm) |
a) Ta có \({(3x + 1)^{11}} = \sum\limits_{k = 0}^{11} {C_{11}^k{3^{11 - k}}{x^{11 - k}}} \) Ycbt \(11 - k = 7 \Leftrightarrow k = 4\) Vậy hệ số x7 trong khai triển là \(C_{11}^4{3^7} = 721710.\) |
0.5 0.25 0.25 |
|
b) Ta có \({(\frac{1}{3} + x)^n} = \sum\limits_{k = 0}^n {C_n^k{{(\frac{1}{3})}^{n - k}}{x^k}} \) \(C_n^7{\left( {\frac{1}{3}} \right)^{n - 7}} = 9C_n^5{\left( {\frac{1}{3}} \right)^{n - 5}}\) \( \Leftrightarrow C_n^7 = C_n^5 \Leftrightarrow n - 7 = 5 \Leftrightarrow n = 12.\) |
0.25
0.25 |
|
|
3 (2 điểm)
|
a) \(\left| \Omega \right| = C_{14}^2 = 91\) Gọi A biến cố chọn được hai viên bi cùng màu \(\left| {{\Omega _A}} \right| = C_9^2 + C_5^2 = 46\) \(P(A) = \frac{{46}}{{91}}\) |
0.25 0.5 0.25 |
|
b) \(\left| \Omega \right| = C_{14}^2 = 91\) Gọi B biến cố “ chọn 2 viên bi khác màu và tổng số ghi trên hai bi là số lẻ” \(\left| {{\Omega _B}} \right| = C_5^1C_3^1 + C_4^1C_2^1 = 23.\) \(P(B) = \frac{{23}}{{91}}\) |
0.25
0.5 0.25 |
|
|
4 (2 điểm) |
a) \({T_{\overrightarrow u }}(A) = A'(x';y'){\rm{ }}\) \(\begin{array}{l} \left\{ \begin{array}{l} x' = x + a\\ y' = y + b \end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l} x' = 2\\ y' = 2 \end{array} \right. \Rightarrow A'(2;2) \end{array}\) |
0.5
0.5 |
|
b) \({Đ_{oy}}\left( C \right) = \left( {{C_1}} \right){_{oy}}\left( I \right) = {I_1}\left( {x';y'} \right)\) \(\left\{ {\begin{array}{*{20}{c}} {x' = - 3}\\ {y' = - 1} \end{array} \Leftrightarrow \left( {{C_1}} \right)\left\{ \begin{array}{l} {I_1}\left( { - 3; - 1} \right)\\ {R_1} = R = 4 \end{array} \right.} \right.\) \(V\left( {O; - 2} \right)\left( {{C_1}} \right) = \left( {C'} \right) \Rightarrow V\left( {O; - 2} \right)\left( {{I_1}} \right) = {I_1}\left( {x';y'} \right)\) \(\left\{ {\begin{array}{*{20}{c}} {x' = 6}\\ {y' = 2} \end{array}\left( {{C_1}} \right)\left\{ {\begin{array}{*{20}{c}} {I'\left( {6;2} \right)\;}\\ {R' = 8} \end{array}} \right.} \right.\) Phương trình (C’) \({\left( {x - 6} \right)^2} + {\left( {y - 2} \right)^2} = 64\) |
0.25
0.25
0.25 0.25 |
|
|
5 (2 điểm) |
\(\left\{ \begin{array}{l} S \in \left( {SAC} \right)\\ S \in \left( {SBD} \right) \end{array} \right.\) Suy ra S điểm chung thứ nhất. Gọi O là giao điểm AC và BD nên O là điểm chung của hai mặt phẳng. \( \Rightarrow (SAC) \cap (SBD) = SO\) Tương tự ta có S là điểm chung thứ nhất của (SAB) và (SCD) \(\left. \begin{array}{l} AB//CD\\ AB \subset (SAB)\\ CD \subset (SCD) \end{array} \right\} \Rightarrow (SAB) \cap (SCD) = d\left( {S \in d,d//AB} \right)\) |
0.25
0.25
0.25
0.25 |
|
Gọi G giao điểm AC và DN, suy ra G là trọng tâm tam giác ABD. Gọi I là giao điểm AM và SG. Ta có \(I \in AM\) và \(I \in SG \subset (SDN) \Rightarrow I = AM \cap (SDN)\) Gọi E là trung điểm GC. Ta có ME là đường trung bình tam giác SGC. Tương tự IG là đường trung bình tam giác AME. Vậy \(\frac{{AI}}{{AN}} = \frac{1}{2}\) |
0.25
0.25 0.25
0.25 |
2. Đề thi học kì 1 môn Toán 11 số 2
TRƯỜNG THPT NAM KỲ KHỞI NGHĨA
ĐỀ THI HK1
NĂM HỌC: 2020-2021
MÔN: TOÁN – LỚP 11
Thời gian: 60 phút (không kể thời gian giao đề)
Phần I. Trắc nghiệm (2,0 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm.
Câu 1: Tập xác định D của hàm số \(y = 2\sin \left( {x - \frac{\pi }{3}} \right)\)
A. \(D = \left[ { - 1;1} \right]\)
B. \(D = \left[ { - 2;2} \right]\)
C. D = R
D. D = Z
Câu 2: Tìm giá tị nhỏ nhất M của hàm số \(y = 1 - 2\cos x\).
A. M = - 1
B. M = 1
C. M = 3
D. M = - 3
Câu 3: Trong mặt phẳng tọa độ Oxy, cho điểm M(1;-2). Phép tịnh tiến theo vectơ \(\vec v\left( { - 1;1} \right)\) biến điểm M thành điểm N. Tìm toa độ điểm N.
A. N(0;-1)
B. N(2;-3)
C. N(-2;3)
D. N(-1;0)
Câu 4: Cho tam giác ABC có trọng tâm G. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Phép vị tự nào sau đây biến \(\Delta ABC\) thành \(\Delta NPM\).
A. \({V_{\left( {A;\frac{1}{2}} \right)}}\)
B. \({V_{\left( {M;\frac{1}{2}} \right)}}\)
C. \({V_{\left( {G; - 2} \right)}}\)
D. \({V_{\left( {G; - \frac{1}{2}} \right)}}\)
Câu 5: Có 10 cặp vợ chồng cùng tham dự chương trình Game show truyền hình thực tế. Có bao nhiêu cách chọn ra hai cặp đôi trong 10 cặp vợ chồng trên sao cho hai cặp đôi đó là hai cặp vợ chồng.
A. 19
B. 90
C. 45
D. 190
Câu 6: Trong khai triển của biểu thức \({\left( {{a^2} - \frac{1}{b}} \right)^7}\), số hạng thứ năm là:
A. \( - 35{a^6}{b^{ - 4}}\)
B. \(35{a^6}{b^{ - 4}}\)
C. \( - 21{a^4}{b^5}\)
D. \(21{a^4}{b^5}\)
Câu 7: Cho hình chóp S.ABCD với đáy là tứ giác ABCD. Thiết diện của hình chóp cắt bởi mặt phẳng \((\alpha)\) tùy ý không thể là:
A. Lục giác
B. Tứ giác
C. Ngũ giác
D. Tam giác
Câu 8: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Giao tuyến của 2 mặt phẳng (SAD) và (SBC) là đường thẳng song song với đường thẳng nào sau đây?
A. AC
B. BD
C. AD
D. SC
Phần II. Tự luận (8,0 điểm)
Câu 1 (1,0 điểm): Giải phương trình \(\cos 5x.\cos x = \cos 4x\).
Câu 2 (1,5 điểm): Tìm số hạng không chứa x trong khai triển của biểu thức \({\left( {2x - \frac{1}{{{x^2}}}} \right)^{12}}\).
---Để xem tiếp nội dung và đáp án của Đề thi số 2, các em vui lòng chọn chức năng Xem Online hoặc tải về máy tính---
3. Đề thi học kì 1 môn Toán 11 số 3
TRƯỜNG THPT NGUYỄN THỊ DIỆU
ĐỀ THI HK1
NĂM HỌC: 2020-2021
MÔN: TOÁN – LỚP 11
Thời gian: 60 phút (không kể thời gian giao đề)
Câu 1: (3 điểm) Giải phương trình:
a) \(\sqrt 3 \sin x - \cos x - 2\cos 2x = 0\)
b) \(1 - \sin x + \cos 3x = \cos x - \sin 2x + \cos 2x\)
Câu 2: (1 điểm) Cho 10 học sinh trong đó có 4 nam và 6 nữ. Có bao nhiêu cách chọn một tổ công tác gồm 5 người trong đó có một tổ trưởng và một thủ quỹ đều là nữ đồng thời trong tổ phải có nam.
Câu 3: (1 điểm) Để thành lập đội tuyển học sinh giỏi toán, nhà trường chọn 4 học sinh từ 21 học sinh gồm : 6 học sinh khối 10, 7 học sinh khối 11 và 8 học sinh khối 12. Tính xác suất để trong đội tuyển mỗi khối có ít nhất một học sinh được chọn.
Câu 4: (1 điểm)
Tìm số hạng không chứa x của khai triển \({\left( {2{x^4} - \frac{3}{x}} \right)^n}\)
Biết \(C_n^0 - 3C_n^1 + {3^2}C_n^2 - {3^3}C_n^3 + ... + {( - 1)^n}{.3^n}C_n^n\) = 1024
Câu 5: (1 điểm)
Cho A(-4, 3); B(2, 5); C(5, -2); tìm phương trình đường tròn (C’) là ảnh của đường tròn đường kính AB qua phép vị tự tâm G; k = -2 với G là trọng tâm tam giác ABC.
Câu 6: (3 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD // BC và AD = 2BC. O là giao điểm 2 đường chéo AC, BD và G là trọng tâm \(\Delta SCD\), M là trung điểm SD.
a) Tìm giao tuyến của (SAD) và (SBC). Tìm giao điểm K của BM và (SAC).
b) Chứng minh: OG // (SBC).
c) CK cắt SA tại N. Tính tỉ số \(\frac{{SN}}{{SA}}\).
---Để xem đáp án của Đề thi số 3, các em vui lòng chọn chức năng Xem Online hoặc tải về máy tính---
4. Đề thi học kì 1 môn Toán 11 số 4
TRƯỜNG THPT NGUYỄN THỊ ĐỊNH
ĐỀ THI HK1
NĂM HỌC: 2020-2021
MÔN: TOÁN – LỚP 11
Thời gian: 60 phút (không kể thời gian giao đề)
Câu 1: Đường thẳng \(y = - \frac{1}{2}\) cắt đồ thị của hàm số \(y = \cos x\) tại những điểm có hoành độ nào?
A. \(x = \pm \frac{\pi }{6} + k2\pi ,k \in Z\)
B. \(x = \pm \frac{{2\pi }}{3} + k2\pi ,k \in Z\)
C. \(x = \pm \frac{\pi }{3} + k2\pi ,k \in Z\)
D. \(x = \pm \frac{{2\pi }}{3} + k\pi ,k \in Z\)
Câu 2: Tìm m để phương trình \(m\sin 2x + \sqrt 3 \cos 2x = m + 1\) vô nghiệm?
A. m < 1
B. \(m \ge 1\)
C. \(m \le 1\)
D. m > 1
Câu 3: Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Khi đó giao tuyến của hai mặt phẳng (SAB) và (SCD) là:
A. Đường thẳng qua S và song song với BD
B. Đường thẳng qua S và song song với AD
C. Đường thẳng qua S và song song với AC
D. Đường thẳng qua S và song song với AB
Câu 4: Từ tập \(A = \left\{ {0;1;2;3;4} \right\}\) lập được bao nhiêu số tự nhiên lẻ gồm bốn chữ số đôi một khác nhau?
A. 24
B. 36
C. 48
D. 60
Câu 5: Qua ba điểm không thẳng hàng xác định bao nhiêu mặt phẳng?
A. 1
B. 2
C. 3
D. 4
---Còn tiếp---
5. Đề thi học kì 1 môn Toán 11 số 5
TRƯỜNG THPT TRẦN VĂN GIÀU
ĐỀ THI HK1
NĂM HỌC: 2020-2021
MÔN: TOÁN – LỚP 11
Thời gian: 60 phút (không kể thời gian giao đề)
Câu 1. Trong mặt phẳng tọa độ Oxy, cho điểm M(1;0). Phép quay tâm O góc 90o biến điểm M thành điểm
A. M'(0;2).
B. M'(0;1).
C. M'(1;1).
D. M'(2;0).
Câu 2. Khẳng định nào sau đây là sai?
A. Hàm số y = x + cos x là hàm số chẵn.
B. Hàm số y = sin x là hàm số lẻ.
C. Hàm số y = cos x là hàm số chẵn.
D. Hàm số y = x + sin x là hàm số lẻ.
Câu 3. Tính giá trị biểu thức \(S = C_7^1 + C_7^2 + C_7^3 + C_7^4 + C_7^5 + C_7^6 + C_7^7\).
A. S = 128.
B. S = 127.
C. S = 49.
D. S = 149.
Câu 4. Một câu lạc bộ cầu lông có 26 thành viên. Số cách chọn một ban đại diện gồm một trưởng ban, một phó ban và một thư ký là
A. 13800.
B. 6900.
C. 15600.
D. 1560.
Câu 5. Trong mặt phẳng tọa độ Oxy, cho A(1;2), B(-3;4). Phép tịnh tiến biến điểm A thành điểm B có vectơ tịnh tiến là
A. \(\vec v = \left( {4;2} \right)\).
B. \(\vec v = \left( {-4;2} \right)\).
C. \(\vec v = \left( {4;-2} \right)\).
D. \(\vec v = \left( {-4;-2} \right)\).
---Còn tiếp---
6. Đề thi học kì 1 môn Toán 11 số 6
TRƯỜNG THPT GÒ VẤP
ĐỀ THI HK1
NĂM HỌC: 2020-2021
MÔN: TOÁN – LỚP 11
Thời gian: 60 phút (không kể thời gian giao đề)
A. TRẮC NGHIỆM (3 điểm)
Câu 1. Với \(k \in Z\), tập xác định của hàm số y = tan x là:
A. \(D = R\backslash \left\{ {\frac{\pi }{2} + k2\pi } \right\}\)
B. \(D = R\backslash \left\{ {\frac{\pi }{2} + k\pi } \right\}\)
C. \(D = R\backslash \left\{ {k\pi } \right\}\)
D. \(D = R\backslash \left\{ {k2\pi } \right\}\)
Câu 2. Với \(k \in Z\), chọn công thức nghiệm đúng của phương trình \(\cot x = \cot \alpha \):
A. \(x = \alpha + k2\pi \)
B. \(x = - \alpha + k2\pi \)
C. \(x = \alpha + k\pi \)
D. \(x = - \alpha + k\pi \)
Câu 3. Với \(k \in Z\), chọn nghiệm đúng của phương trình sin x = - 1:
A. \(x = \frac{\pi }{2} + k2\pi \)
B. \(x = \frac{\pi }{2} + k\pi \)
C. \(x = - \frac{\pi }{2} + k\pi \)
D. \(x = - \frac{\pi }{2} + k2\pi \)
Câu 4. Với \(k \in Z\), chọn nghiệm đúng của phương trình \(\tan 3x = \sqrt 3 \).
A. \(x = \frac{\pi }{9} + \frac{{k\pi }}{3}\)
B. \(x = - \frac{\pi }{9} + \frac{{k\pi }}{3}\)
C. \(x = \frac{\pi }{9} + k\pi \)
D. \(x = - \frac{\pi }{9} + k\pi \)
Câu 5. Với \(n,k \in {{\rm N}^*};n \ge k\), chọn công thức đúng ?
A. \(A_n^k = \left( {n - k} \right)!\)
B. \({P_n} = n!\)
C. \(C_n^k = \left( {n + k} \right)!\)
D. \({P_{n + 1}} = \left( {n - 1} \right)!\)
---Còn tiếp---
7. Đề thi học kì 1 môn Toán 11 số 7
Trường THPT Thủ Đức
Số câu: 12 câu trắc nghiệm và 6 câu tự luận
Thời gian: 60 phút (không kể thời gian giao đề)
Năm học: 2020-2021
8. Đề thi học kì 1 môn Toán 11 số 8
Trường THPT Nguyễn Viết Xuân
Số câu: 40câu trắc nghiệm
Thời gian: 60 phút (không kể thời gian giao đề)
Năm học: 2020-2021
9. Đề thi học kì 1 môn Toán 11 số 9
Trường THPT Nguyễn Du
Số câu: 20 câu trắc nghiệm và 3 câu tự luận
Thời gian: 90 phút (không kể thời gian giao đề)
Năm học: 2020-2021
10. Đề thi học kì 1 môn Toán 11 số 10
Trường THPT Nguyễn Thị Minh Khai
Số câu: 23 câu trắc nghiệm và 3 câu tự luận
Thời gian: 90 phút (không kể thời gian giao đề)
Năm học: 2020-2021
-Bấm TẢI VỀ hoặc chọn chức năng XEM ONLINE để xem đầy đủ nội dung các Đề thi 1-10-
Tham khảo thêm
- docx 10 đề thi Học kì 1 môn Toán lớp 11 năm 2019 có đáp án