Lý 12 Bài 3: Con lắc đơn

Gồm một vật nhỏ khối lượng m, treo ở đầu dưới một sợi dây không dãn, khối lượng không đáng kể, chiều dài l, đầu trên sợi dây được treo vào điểm cố định.

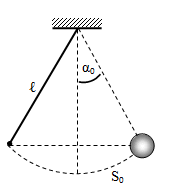
• Các phương trình dao động điều hòa

Li độ cong: s = S₀cos(ωt + φ) (cm, m)

Li độ góc: α = α₀cos(ωt + φ) (độ, rad)

• Chú ý

Con lắc đơn dao động điều hòa khi góc lệch nhỏ và bỏ qua mọi ma sát.

s = l.α và S₀ = l.α₀ với α và α₀ có đơn vị rad.

• Tần số góc: \(\omega = \sqrt {\frac{g}{l}} \)
• Chu kì của con lắc đơn: T = 2π\(\sqrt {\frac{l}{g}} \)
• Tần số của con lắc đơn: f =\(\frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \)

Nhận xét: Khi con lắc dao động điều hòa thì chu kì không phụ thuộc khối lượng vật nặng và cũng không phụ thuộc biên độ.

a. Động năng của con lắc đơn: \({{\rm{W}}_d} = \frac{1}{2}m{v^2}\)

b. Thế năng của con lắc đơn: \({{\rm{W}}_t} = mgl(1 - \cos \alpha )\)

c. Cơ năng của con lắc đơn: \({\rm{W = }}\frac{1}{2}m{v^2} + mgl(1 - \cos \alpha ) = mgl(1 - \cos {\alpha _0}) = \frac{1}{2}mv_{\max }^2\)

Nếu bỏ qua ma sát thì cơ năng của con lắc được bảo toàn.

• Chú ý: Công thức đúng với mọi li độ góc α ≤ 900α ≤ 900

Một con lắc đơn có chiều dài l = 16 cm. Kéo con lắc lệch khỏi vị trí cân bằng một góc 90^o rồi thả nhẹ. Bỏ qua mọi ma sát , lấy g = 10 m/s², π² = 10. Chọn gốc thời gian lúc thả vật, chiều dương là chiều chuyển động ban đầu của vật. Viết phương trình dao động của vật theo li độ góc.

Hướng dẫn giải

Ta có: ω =\(\sqrt {\frac{g}{l}} \)= 2,5 rad/s

cosφ  = \(\frac{\alpha }{{{\alpha _0}}}\) = \(\frac{{ - {\alpha _0}}}{{{\alpha _0}}}\) = −1 = cosπ ⇒ φ = π rad

Vậy: α = 0,157cos(2,5π+π) rad

Một con lắc đơn dao động điều hoà theo phương trình li độ góc α = 0,1cos(2πt+π4) rad. Trong khoảng thời gian 5,25 s. Tính từ thời điểm con lắc bắt đầu dao động, có bao nhiêu lần con lắc có độ lớn vận tốc bằng 1/2 vận tốc cực đại của nó?

Hướng dẫn giải

Trong một chu kỳ dao động có 4 lần \(v = \frac{{{v_{\max }}}}{2}\)  tại vị trí \({{\rm{W}}_d} = \frac{{\rm{W}}}{4}\)  ⇒  \({\rm{W}}t = \frac{3}{4}{{\rm{W}}_{t\max }}\)

Tức là lúc li độ 

α = \(\pm \frac{{{a_{\max }}\sqrt 3 }}{2}\) với chu kì con lắc đơn đã cho T = 1s

Ta có t = 5,25 s = 5T + 14T

Khi t = 0 s thì α₀ = 0,1cos( \(\frac{\Pi }{4}\)) =  \(\frac{{{a_{\max }}\sqrt 2 }}{2}\); vật chuyển động theo chiều âm về VTCB

Sau 5 chu kì vật trở lại vị trí ban đầu, sau T/4 tiếp vật chưa qua được vị trí α = \(- \frac{{{a_{\max }}\sqrt 3 }}{2}\)

Vậy: Trong khoảng thời gian 5,25 s tính từ thời điểm con lắc bắt đầu dao động, con lắc có độ lớn vận tốc bằng 1/2 vận tốc cực đại của nó 20 lần.

Câu 1: Một lò xo có chiều dài tự nhiên l₀ = 20 cm. Khi treo vật có khối lượng m = 100 g thì chiều dài của lò xo khi hệ cân bằng l = 24 cm. Tính chu kì dao động tự do của hệ.

Câu 2: Một con lắc lò xo dao động thẳng đứng. Khi vật có khối lượng m = 0,2 kg. Trong 20 s con lắc thực hiện được 50 dao động. Tính độ cứng của lò xo.

Câu 3: Vật nặng gắn vào lò xo có độ cứng k = 100 N/m, dao động điều hòa, thực hiện được 10 dao động trong 4 s. Tính chu kì dao động và khối lượng của vật. Lấy g = 10 m/s².

Câu 4 : Một vật có khối lượng m = 100 g gắn vào một lò xo nằm ngang. Con lắc lò xo này dao động điều hòa với tần số f = 10 Hz. Tính độ cứng của lò xo. 

Câu 1: Cho một con lắc đơn có dây treo dài , quả nặng khối lượng m, kéo con lắc lệch khỏi vị trí cân bằng một góc  rồi thả nhẹ cho vật dao động. Bỏ qua mọi ma sát, chọn gốc thế năng tại vị trí cân bằng của vật. Cơ năng của con lắc trong quá trình dao động là:

A. \(mg\ell (1 - \cos {\alpha _0})\)          B. mg\(\ell \)cos\({\alpha _0}\)                 C. mg\(\ell \)                           D. mg\(\ell \)(1 + cos )

Câu 2: Một con lắc đơn có chiều dài 1 m, khối lượng quả nặng bằng100 (g) dao động với biên độ góc 30⁰ tại nơi có g = 10 m/s². Bỏ qua mọi ma sát. Cơ năng của con lắc đơn là:

A. \(\frac{{2 - \sqrt 3 }}{2}{\kern 1pt} {\kern 1pt} {\kern 1pt} J\)                          B. \(\frac{5}{{36}}{\kern 1pt} {\kern 1pt} {\kern 1pt} J\)                        C. \(0,5{\kern 1pt} {\kern 1pt} {\kern 1pt} J\)                         D. \(\frac{{125}}{9}{\kern 1pt} {\kern 1pt} {\kern 1pt} J\)

Câu 3: Một con lắc đơn có khối lượng của vật nặng là m = 200 g dao động với phương trình s = 10sin2t (cm). Ở thời điểm  s, con lắc có động năng là:

A. 10^-2 J                             B. 10 mJ                      C. 1 J                              D. 1 mJ

Câu 4: Một con lắc đơn dao động điều hoà với biên độ góc . Với li độ góc  bằng bao nhiêu thì động năng của con lắc gấp 2 lần thế năng?

A. \(\alpha = \pm 2,{89^o}\)                   B. \(\alpha = 3,{45^o}\)               C. \(\alpha = \pm 3,{45^o}\)               D. \(\alpha = 2,{89^o}\)

4. Kết luận

Qua bài con lắc đơn này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như : 

• Hiểu được cấu tạo con lắc đơn.
• Viết được phương trình động học của con lắc đơn.
• Điều kiện để vật nặng con lắc đơn dao động điều hòa. Viết được công thức tính chu kì, tần số góc của dao động.
• Viết được công thức tính thế năng, động năng và cơ năng của con lắc đơn.
• Xác định lực kéo về tác dụng vào con lắc đơn.