10 đề thi giữa HK1 môn Toán 12 năm 2021 - 2022 có đáp án

ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 1

MÔN TOÁN 12

NĂM HỌC 2021-2022

I. Tóm tắt lý thuyết

1.1. Giải tích

a) Sự đồng biến, nghịch biến của hàm số

Định nghĩa

Hàm số y = f(x) đồng biến (tăng) trên K ⇔ ∀x1, x2 ∈ K, x1 < x2 thì f(x1) < f(x2).

Hàm số y = f(x) nghịch biến (giảm) trên K ⇔ ∀x1, x2 ∈ K, x1 < x2 thì f(x1) > f(x2).

Quy tắc xét tính đơn điệu của hàm số

 i) Tìm tập xác định

 ii) Tính đạo hàm f'(x). Tìm các điểm xi (i= 1 , 2 ,..., n) mà tại đó đạo hàm bằng 0  hoặc không xác định.

 iii) Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.

 iv) Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

b) Cực trị của hàm số

Quy tắc tìm cực trị của hàm số

- Quy tắc 1:

Bước 1. Tìm tập xác định của hàm số.

Bước 2. Tính f'(x) . Tìm các điểm tại đó f'(x) bằng 0 hoặc f'(x) không xác định.

Bước 3. Lập bảng biến thiên.

Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.

- Quy tắc 2:

Bước 1. Tìm tập xác định của hàm số.

Bước 2. Tính f'(x). Giải phương trình f'(x) và ký hiệu xi (i = 1; 2; 3;...) là các nghiệm của nó.

Bước 3. Tính f"(x) và f"(xi).

Bước 4. Dựa vào dấu của f"(xi) suy ra tính chất cực trị của điểm xi.

c) Giá trị lớn nhất - Giá trị nhỏ nhất của hàm số

Tìm GTLN - GTNN của hàm sô trên một khoảng, nửa khoảng.

Tìm GTLN - GTNN của hàm số trên một đoạn.

d)  Khảo sát sự biến thiên và vẽ đồ thị hàm số

Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc ba.

Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc bốn (trùng phương)

Khảo sát sự biến thiên và vẽ đồ thị hàm số phân thức bậc nhất/bậc nhất (hàm nhất biến).

e) Bài toán về sự tương giao của đồ thị hàm số

Tìm số giao điểm của hai đường (C1):y=f(x) và (C2):y=g(x).

Biện luận theo m nghiệm của phương trình f(x)=m.

1.2. Hình học

a) Khối lăng trụ và khối chóp

Khối lăng trụ là phần không gian được giới hạn bởi một hình lăng trụ kể cả hình lăng trụ ấy.

Khối chóp là phần không gian được giới hạn bởi một hình chóp kể cả hình chóp ấy.

Khối chóp cụt là phần không gian được giới hạn bởi một hình chóp cụt kể cả hình chóp cụt ấy.

b) Khái niệm về hình đa diện,  khối đa diện

c) Phép dời hình và sự bằng nhau giữa các khối đa diện

-  Trong không gian quy tắc đặt tương ứng mỗi điểm \(M\) với điểm \(M’\) xác định duy nhất được gọi là một phép biến hình trong không gian.

-  Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm tùy ý.

-  Thực hiện liên tiếp các phép dời hình sẽ được một phép dời hình.

-  Phép dời hình biến một đa diện thành một đa diện, biến các đỉnh, cạnh, mặt của đa diện này thành đỉnh, cạnh, mặt tương ứng của đa diện kia.

d) Lý thuyết khối đa diện lồi và khối đa diện đều

    Chỉ có năm khối đa diện đều. Đó là:

    - Loại {3; 3}: khối tứ diện đều.

    - Loại {4; 3}: khối lập phương.

    - Loại {3; 4}: khối bát diện đều.

    - Loại {5; 3}: khối 12 mặt đều.

    - Loại {3; 5}: khối 20 mặt đều.

e) Thể tích của khối đa diện

+ Công thức tính thể tích khối chóp

    Trong đó: S là diện tích đáy, h là chiều cao khối chóp.

+ Công thức tính thể tích khối lăng trụ

    Trong đó: B là diện tích đáy, h là hiều cao khối lăng trụ

+ Thể tích khối hộp chữ nhật: V = abc

    Trong đó: a, b, c là ba kích thước của khối hộp chữ nhật.

+ Thể tích khối lập phương: V = a3

    Trong đó a là độ dài cạnh của hình lập phương.

2. Bài tập minh họa

2.1. Bài tập tự luận

Câu 1: Cho hàm số y = 2x2 + 2mx + m - 1 có đồ thị là (Cm), m là tham số.

a) Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m = -1

b) Xác định m để hàm số:

i) Đồng biến trên khoảng (-1; +∞)

ii) Có cực trị trên khoảng (-1; +∞)

c) Chứng minh rằng (Cm) luôn cắt trục hoành tại hai điểm phân biệt với mọi m.

Hướng dẫn giải

a) Với m = 1 ta được hàm số: y = 2x2 + 2x

- TXĐ: D = R,

- Sự biến thiên:

+ Chiều biến thiên: y' = 4x + 2

y' = 0 ⇔ x = -1/2

+ Bảng biến thiên:

+ Bảng biến thiên:

Kết luận: Hàm số nghịch biến trên (-∞; -1/2), đồng biến trên (-1/2; +∞).

Đồ thị hàm số có điểm cực tiểu là (-1/2; -1/2)

- Đồ thị:

Ta có: 2x2 + 2x = 0 ⇔ 2x(x + 1) = 0

⇒ x = 0; x = -1

+ Giao với Ox: (0; 0); (-1; 0)

+ Giao với Oy: (0; 0)

b) Xét hàm số y = 2x2 + 2mx + m - 1

y' = 4x + 2m = 2(2x + m)

y' = 0 ⇒ x = -m/2

Ta có bảng xét biến thiên :

Từ bảng biến thiên ta thấy :

- Hàm số đồng biến trên khoảng (-1; +∞)

- Hàm số có cực trị trên khoảng (-1; +∞)

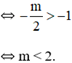
c) Nhận thấy: 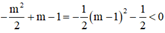 với mọi m.

Suy ra, giá trị cực tiểu luôn nhỏ hơn 0 với mọi m.

Dựa vào bảng biến thiên suy ra đường thẳng y = 0 (trục hoành) luôn cắt đồ thị hàm số tại 2 điểm phân biệt (đpcm).

Câu 2: Cho hình lăng trụ và hình chóp có diện tích đáy và chiều cao bằng nhau. Tính tỉ số thể tích của chúng.

Hướng dẫn giải

Gọi S là diện tích đáy và h là chiều cao của hình lăng trụ và của hình chóp, ta có:

- Thể tích khối lăng trụ là: V1 = Sh

- Thể tích khối chóp là: V2= Sh/3

Vậy V1/ V2=3Sh/Sh = 3

Câu 3: Cho khối hộp ABCD.A’B’C’D’. Gọi E và F theo thứ tự là trung điểm của các cạnh BB’ và DD’. Mặt phẳng (CEF) chia khối hộp trên làm hai khối đa diện. Tính tỉ số thể tích của hai khối đa diện đó.

Hướng dẫn giải

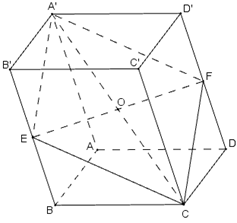
Gọi O là tâm hình hộp và tâm của hình bình hành BB’D’D. Khi đó O là trung điểm của EF.

Ta có: A’ ∈ CO (1)

CO ⊂ mp(CEF)(2)

Mặt khác A’E // CF, A’F // CE

Nên mp(CEF) cắt hình hộp theo thiết diện là hình bình hành A’ECF.

mp(CEF) chia hình hộp ABCD.A’B’C’D’ thành hai khối đa diện (Đ) và (Đ’).

Gọi (Đ) là khối đa diện có các đỉnh là A, B, C, D, A’, E, F và (Đ’) là khối đa diện còn lại.

Phép đối xứng qua tâm O biến các đỉnh A, B, C, D, A’, E, F của đa diện (Đ) lần lượt thành các đỉnh C’, D’, A’, B’, C, F, E của khối da diện (Đ’)

Suy ra phép đối xứng qua tâm O biến (Đ) thành (Đ’), nghĩa là hai hình đa diện (Đ) và (Đ’) bằng nhau.

Vậy tỉ số thể tích của (Đ) và (Đ’) bằng 1.

2.2. Bài tập trắc nghiệm

Câu 1: Giá trị của \(\lim _{x \rightarrow 1}\left(3 x^{2}-2 x+1\right)\) bằng:

A. 2 

B. 3

C. \(+\infty\)

D. 1

Câu 2: Tìm số hạng không chứa x trong khai triển của \(\left(x \sqrt{x}+\frac{1}{x^{4}}\right)^{n},\) với x > 0, nếu biết rằng \(C_{n}^{2}-C_{n}^{1}=44\)

A. 525

B. 485

C. 165

D. 238

Câu 3: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB và AC, E là điểm trên cạnh CD với ED = 3E C. Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD là.

A. Tam giác MNE.

B. Tứ giác MNEF với F là điểm bất kì trên cạnh BD.

C. Hình bình hành MNEF với F là điểm trên cạnh BD mà EF // BC.

D. Hình thang MNEF với F là điểm trên cạnh BD mà EF // BC.

Câu 4: Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau lập từ các chữ số 1, 2, 3, 4, 5?

A. 900 

B. 60 

C. 125 

D. 20 

Câu 5: Khi cắt hình chóp tứ giác S.ABCD bởi một mặt phằng, thiết diện không thể là hình nào?

A. Tứ giác.

B. Tam giác.

C. Lục giác.

D. Ngũ giác.

Câu 6: Tìm giá trị lớn nhất M của hàm số \(y=2 x^{3}+3 x^{2}-12 x+2\) trên đoạn [-1 ; 2].

A. M = 10.

B. M = 6.

C. M = 11.

D. M=15.

Câu 7: Cho hình lăng trụ đều BAC.A'B'C' có cạnh đáy bằng 2a, cạnh bên bằng a. Tính góc giữa hai mặt phẳng \(\left(A B^{\prime} C^{\prime}\right)\) và \(\left(A^{\prime} B^{\prime} C^{\prime}\right)\).

A. \(\arccos \frac{\sqrt{3}}{4}\)

B. \(\arcsin \frac{\sqrt{3}}{4}\)

C. \(\frac{\pi}{3}\).

D. \(\frac{\pi}{6}\).

Câu 8: Cho cấp số cộng có tổng n số hạng đầu là \(S_{n}=4 n^{2}+3 n, n \in \mathbb{N}^{*}\) thì số hạng thứ 10 của cấp số cộng là

A. \(u_{10}=79\)

B. \(u_{10}=71\)

C. \(u_{10}=95\)

D. \(u_{10}=87\)

.........

---(Để xem tiếp nội dung của đề thi các em vui lòng xem tại online hoặc đăng nhập để tải về máy)--- 

Câu 1. Gọi M, N là giao điểm của đồ thị hàm số \(y=\frac{x+1}{x-2}\) và đường thẳng d: y = x + 2. Hoành độ trung điểm I của đoạn MN là

A. \(-\frac{5}{2}\)

B. \(-\frac{1}{2}\)

C. 1

D. \(\frac{1}{2}\).

Câu 2. Tâm đối xứng của đồ thị hàm số nào sau đây cách gốc tọa độ một khoảng lớn nhất?

A. \(y=\frac{2x-1}{x+3}\)                 

B. \(y=\frac{1-x}{1+x}\) 

C. \(y=2{{x}^{3}}-3{{x}^{2}}-2\) 

D. \(y=-{{x}^{3}}+3x-2\) 

Câu 3. Cho hàm số \(f(x)={{x}^{3}}+a{{x}^{2}}+bx+c\). Mệnh đề nào sau đây sai ?

A. Đồ thị hàm số luôn có điểm đối xứng.

B. Đồ thị hàm số luôn cắt trục hoành

C. Hàm số luôn có cực trị.

D. \(\underset{x\to +\infty }{\mathop{\lim }}\,f(x)=+\infty \text{ }\).

Câu 4. Cho hàm số \(y=\frac{x-1}{x+2}\) có đồ thị (C). Tiếp tuyến của (C) tại giao điểm của (C) với trục hoành có phương trình là:

A. y = 3x                     

B. y = x – 3   

C. y = 3x – 3              

D. \(y=\frac{1}{3}(x-1)\).

Câu 5. Cho hàm số y = f(x) có đồ thị như hình vẽ dưới đây.

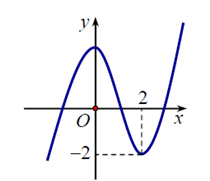
Mệnh đề nào dưới đây đúng ?

A. Hàm số có giá trị cực tiểu bằng 2.

B. Hàm số đạt cực đại tại x = 0 và giá trị cực tiểu tại x = 2.

C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng – 2 .

D. Hàm  số có ba điểm cực trị.

Câu 6. Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số \(y=\frac{2x}{x-2}\).

A. 2y – 1= 0             

B. 2x – 1 = 0     

C. x – 2 = 0              

D. y – 2 = 0.

Câu 7. Cho hàm số \(y=\frac{1}{4}{{x}^{4}}-2{{x}^{2}}+3\). Khẳng định nào sau đây đúng ?

A. Hàm số nghịch biến trên khoảng \((-2;0),(2;+\infty )\).

B. Hàm số nghịch biến trên khoảng \((-\infty ;-2),(0;2)\).

C. Hàm số nghịch biến trên khoảng \((-\infty ;0)\).

D. Hàm số đồng biến trên khoảng \((-\infty ;-2),(2;+\infty )\).        

Câu 8. Đồ thị sau đây là của hàm số nào ?

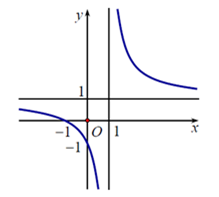
A. \(y=\frac{2x-3}{2x-2}\)

B. \(y = \dfrac{x}{{x - 1}}\)

C. \(y = \dfrac{{x - 1}}{{x + 1}}\)

D. \(y = \dfrac{{x + 1}}{{x - 1}}\)

Câu 9. Tìm giá trị lớn nhất của hàm số \(y = \dfrac{{3x - 1}}{ {x - 3}}\) trên đoạn [0 ; 2].

A. \(-\dfrac {1 }{ 3}\)                             

B. – 5   

C. 5                                 

D. \(\dfrac{1 }{3}\)

Câu 10. Hàm số \(y=\frac{1}{3}{{x}^{3}}-2{{x}^{2}}+3x\text{ }\) nghịch biến trên khoảng nào trong những khoảng sau đây?

A. (1 ; 4)                        

B. (1 ; 3)

C. (-3 ; -1)                     

D. (- 1 ; 3)

..........

---(Để xem tiếp nội dung của đề thi các em vui lòng xem tại online hoặc đăng nhập để tải về máy)--- 

TRƯỜNG TRƯỜNG THPT NGUYỄN CÔNG TRỨ

ĐỀ THI GIỮA HK1

NĂM HỌC: 2021-2022

MÔN: TOÁN 12

Câu 1: 

Cho hàm số y=f(x) có đạo hàm trên R và có bảng xét dấu \({f}'(x)\) như sau

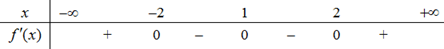
Mệnh đề nào sau đây đúng?

A. Hàm số y=f(x) đồng biến trên khoảng \((-2\,;\,1).\)

B. Hàm số y=f(x) đồng biến trên khoảng \((-\infty \,;\,2).\)

C. Hàm số y=f(x) nghịch biến trên khoảng \((-2\,;\,2).\)

D. Hàm số y=f(x) nghịch biến trên khoảng \((2\,;\,+\infty ).\)

Câu 2: Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau

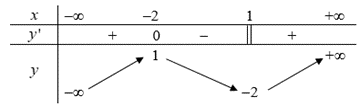
Mệnh đề nào sau đây đúng?

A. Hàm số y=f(x) đạt cực tiểu tại x=-2.                

B. Hàm số y=f(x) đạt cực tiểu tại x=1.                 

C. Hàm số y=f(x) đạt cực đại tại x=1.                  

D. Hàm số y=f(x) có đúng một điểm cực trị.

Câu 3:  Đường tiệm cận đứng của đồ thị hàm số \(y=\frac{3x-2}{1-2x}\) là đường thẳng

A. \(x=\frac{1}{2}.\)             

B. \(y=-\frac{3}{2}.\)        

C. \(x=\frac{2}{3}.\)        

D. \(x=-\frac{1}{2}.\)

Câu 4:  Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?

​

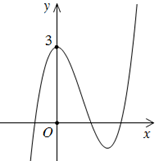
A. \(y={{x}^{4}}-3{{x}^{2}}+3\).

B. \(y={{x}^{3}}-3{{x}^{2}}-3\).

C. \(y=-{{x}^{3}}+3{{x}^{2}}+3\).

D. \(y={{x}^{3}}-3{{x}^{2}}+3\).

Câu 5:   Với a là số thực dương tùy ý, \({{a}^{2}}.{{a}^{\frac{1}{3}}}\) bằng

A. \({{a}^{\frac{2}{3}}}.\)

B. \({{a}^{\frac{7}{3}}}.\)                                        

C. \({{a}^{\frac{5}{3}}}.\)    

D. \({{a}^{\frac{4}{3}}}.\)

Câu 6:  Nếu \(x,\,\,y\) là hai số thực dương tùy ý thỏa mãn \(\log x\ge \log y\) thì

A. \(x\le y.\)               

B. \(x>y.\)                           

C. \(x < y\)

D. \(x\ge y.\)

Câu 7: Tập xác định D của hàm số \(y={{\log }_{5}}(x-3)\) là

A. \(D=[3\,;\,+\infty ).\)         

B. \(D=\left[ 0\,;\,+\infty  \right).\)                             

C. \(D=(3\,;\,+\infty ).\) 

D. \(D=(0\,;\,+\infty ).\) 

Câu 8: Đạo hàm của hàm số \(f(x)={{5}^{x}}\) là

A. \({f}'(x)={{5}^{x}}.ln5.\)      

B. \({f}'(x)=x{{.5}^{x-1}}.\)          

C. \({f}'(x)=\frac{{{5}^{x}}}{\ln 5}\cdot \)      

D. \({f}'(x)=x.\ln 5.\)

Câu 9:  Mệnh đề nào sau đây sai?

A. Số cạnh của một hình lăng trụ luôn lớn hơn số đỉnh của nó.

B. Số đỉnh của một hình lăng trụ luôn lớn hơn 5.

C. Số cạnh của một hình chóp luôn lớn hơn số mặt của nó.

D. Số mặt của một hình chóp luôn lớn hơn 4.

Câu 10:  Gọi M là trung điểm cạnh \({B}'{C}'\) của khối lăng trụ \(ABC.{A}'{B}'{C}'\). Mặt phẳng nào sau đây chia khối lăng trụ \(ABC.{A}'{B}'{C}'\) thành hai khối lăng trụ?

A. \((MAB).\)   

B. \((MA{A}').\)         

C. \((MA'B).\)    

D. \((MAB').\) 

..........

---(Để xem tiếp nội dung của đề thi các em vui lòng xem tại online hoặc đăng nhập để tải về máy)--- 

TRƯỜNG TRƯỜNG THPT DUY TÂN

ĐỀ THI GIỮA HK1

NĂM HỌC: 2021-2022

MÔN: TOÁN 12

Câu 1: Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau

Đồ thị của hàm số \(y=\left| f\left( x \right) \right|\) có bao nhiêu điểm cực trị?

A. 2                           

B. 4                              

C. 5                            

D. 3

Câu 2: Hàm số nào sau đây nghịch biến trên mỗi khoảng xác định của nó?

A. \(y=-{{x}^{3}}-2{{x}^{2}}+3.\)  

B. \(y=\frac{x+1}{x-2}.\)                    

C. \(y=\frac{2x+1}{x+2}.\)              

D. \(y=2{{x}^{3}}+3{{x}^{2}}+10x-1.\)

Câu 3: Đường cong hình bên là đồ thị của hàm số \(y=\frac{\text{ax}+b}{cx+d}\), với a, b, c, d là các số thực. Mệnh đề nào dưới đây đúng?

A. \(\left( 1;3;-5 \right).\)

B. \(y'>0\,\,;\,\,\forall x\ne 1\).                                  

C. \(y'<0\,\,;\,\,\forall x\in \mathbb{R}.\)                      

D. \(y'<0\,\,;\,\,\forall x\ne 1\).

Câu 4: Cho hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\) có đồ thị như hình bên. Mệnh đề nào dưới đây là đúng?

A. \(a<0,b>0,c<0.\)         

B. \(a>0,b<0,c>0\)         

C. \(a>0,b<0,c<0\).         

D. \(a>0,b>0,c<0\).

Câu 5: Cho hàm số y=f(x) xác định và liên tục trên R và bảng biến thiên sau.

Khẳng định nào sau đây sai?

A. Đường thẳng y=-2 cắt đồ thị hàm số tại 3 điểm phân biệt.  

B. Hàm số có điểm cực tiểu là x=-2.

C. \(f(x)={{x}^{3}}+3{{x}^{2}}-4\).                                                            

D. Hàm số nghịch biển trên khoảng (-2;0).

Câu 6: Cho \(a=1+{{2}^{-x}}\), \(b=1+{{2}^{x}}\). Biểu thức biểu diễn b theo a là:

A. \(\frac{a+2}{a-1}\).     

B. \(\frac{a-2}{a-1}\).       

C. \(\frac{a-1}{a}\).         

D. \(\frac{a}{a-1}\).

Câu 7: Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình bên. Phát biểu nào sau đây là đúng?

A. Hàm số đạt cực đại tại x=1\                             

B. Giá trị cực tiểu của hàm số là -1

C. Hàm số đạt cực tiểu tại x=1                             

D. Hàm số có 3 cực trị    .

Câu 8: Cho hàm số \(y=f\left( x \right)\) có đạo hàm trên R và có đồ thị là đường cong như hình vẽ dưới đây.

Đặt \(g\left( x \right)=f\left( f\left( x \right) \right)\). Số nghiệm của phương trình \({{g}^{/}}\left( x \right)=0\) là :

A. 6                            

B. 7                             

C. 5                             

D. 8

Câu 9: Đồ thị như hình vẽ là đồ thị của hàm số nào dưới đây?

A. \(y=-{{x}^{3}}-\text{3}{{x}^{2}}-4.\)                   

B. \(y={{x}^{3}}-\text{3}{{x}^{2}}+4\)

C. \(y={{x}^{3}}-\text{3}{{x}^{2}}-4\)                     

D. \(y=-{{x}^{3}}\text{+3}{{x}^{2}}-4\)

Câu 10: Để đường thẳng \(d:y=x-m+2\) cắt đồ thị hàm số \(y=\frac{2x}{x-1}\) \(\left( C \right)\) tại hai điểm phân biệt A và B sao cho độ dài AB ngắn nhất thì giá trị của m thuộc khoảng nào?

A. \(m\in \left( -4;-2 \right)\).

B. \(m\in \left( 2;4 \right)\).   

C. \(m\in \left( -2;0 \right)\). 

D. \(m\in \left( 0;2 \right)\).

..........

---(Để xem tiếp nội dung của đề thi các em vui lòng xem tại online hoặc đăng nhập để tải về máy)--- 

TRƯỜNG TRƯỜNG THPT NGUYỄN VIẾT XUÂN

ĐỀ THI GIỮA HK1

NĂM HỌC: 2021-2022

MÔN: TOÁN 12

Câu 1: Cho hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\) có đồ thị như hình bên. Mệnh đề nào dưới đây là đúng?

A. a>0,b<0,c>0.          

B. a>0,b>0,c<0.         

C. a>0,b<0,c<0.              

D. a<0,b>0,c<0.

Câu 2: Cho hình chóp S.ABC có thể tích bằng V. Gọi G là trọng tâm tam giác SBC. Mặt phẳng \({(\alpha )}\) đi qua hai điểm A,G và song song với BC. Mặt phẳng \({(\alpha )}\) cắt các cạnh SB,SC lần lượt tại các điểm M và N. Thể tích khối chóp S.AMN bằng

A. \(\frac{V}{9}\).            

B. \(\frac{V}{2}\).            

C. \(\frac{4V}{9}\).          

D. \(\frac{V}{4}\).

Câu 3: Một chất điểm chuyển động có phương trình \({S=2{{t}^{4}}+6{{t}^{2}}-3t+1}\) với t tính bằng giây (s) và S tính bằng mét (m). Hỏi gia tốc của chuyển động tại thời điểm \({t=3(s)}\) bằng bao nhiêu?

A. 76 \({\left( \text{m/}{{\text{s}}^{\text{2}}} \right)}\).                           

B. 228 \({\left( \text{m/}{{\text{s}}^{\text{2}}} \right)}\).                

C. 64 \({\left( \text{m/}{{\text{s}}^{\text{2}}} \right)}\).                             

D. 88 \({\left( \text{m/}{{\text{s}}^{\text{2}}} \right)}\).

Câu 4: Cho hàm số \(y=f\left( x \right)\) liên tục trên đoạn \(\left[ -1;3 \right]\) và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \(\left[ -1;3 \right]\). Giá trị của M-m bằng

A. 4.                             

B. 5.                             

C. 0.                             

D. 1.

Câu 5: Cho hàm số \(y=f\left( x \right)$\). Đồ thị hàm số \(y={f}'\left( x \right)\) trên khoảng \(\left( -1;2 \right)\) như hình vẽ bên. Số điểm cực đại của hàm số \(y=f\left( x \right)\) trên khoảng \(\left( -1;2 \right)\) là

A. 2.                             

B. 1.                           

C. 0.                             

D. 3

Câu 6: Một khối lập phương có cạnh bằng \(a\left( cm \right)\). Khi tăng kích thước của mỗi cạnh thêm 2cm thì thể tích của khối lăng trụ tăng thêm \(98c{{m}^{3}}\). Giá trị a bằng:

A. 3cm                       

B. 6cm                       

C. 4cm                        

D. 5cm

-----Còn tiếp-----

2.5. Đề thi giữa HK1 môn Toán 12 – Số 5

TRƯỜNG TRƯỜNG THPT VÕ TRƯỜNG TOẢN

ĐỀ THI GIỮA HK1

NĂM HỌC: 2021-2022

MÔN: TOÁN 12

Câu 1: Cho hàm số \(y = {x^3} + 3x + 2\). Mệnh đề nào dưới đây đúng ?

A. Hàm số đồng biến trên khoảng (−∞; 0) và nghịch biến trên khoảng (0; + ∞) .

B. Hàm số đồng biến trên khoảng (−∞;  + ∞) .

C. Hàm số nghịch biến trên khoảng (− ∞;  + ∞) .

D. Hàm số nghịch biến trên khoảng (− ∞; 0) và đồng biến trên khoảng (0; + ∞)

Câu 2: Tìm tất cả giá trị thực của m để hàm số \(y = \frac{1}{3}{x^3} - (m + 1){x^2} + {m^2}x - 1\) có 2 cực trị:

A. m > -1/2

B. \(m \le - 1/2\)

C. \(m \le 1/2\)

D. m > ½

Câu 3: Cho hàm số \(y = {x^4} - 2{x^2}\). Mệnh đề nào dưới đây đúng ?

A. Hàm số nghịch biến trên khoảng  (−∞;  − 2)

B. Hàm số đồng biến trên khoảng  (−∞;  − 2)

C. Hàm số đồng biến trên khoảng  (−1; 1) .             

D. Hàm số nghịch biến trên khoảng  (−1; 1) .

Câu 4: Tất cả giá trị của m để hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + ({m^2} - m)x + 1\) có 1 cực đại và 1 cực tiểu là:

A. -1/2 < m <0

B. 0 < m < 1/2

C.  m > 0

D.  m < 0  

Câu 5: Hàm số \(f(x) = 2{x^4} + 1\) đồng biến trên khoảng nào?

A. \(( - \infty ; - \frac{1}{2})\).

B. \(( - \infty ;0)\)

C. \(( - \frac{1}{2}; + \infty )\) 

D. \((0; + \infty )\) 

Câu 6: Số điểm cực đại của đồ thị hàm số \(f(x)=\frac{1}{4}{{x}^{4}}+2{{x}^{2}}-4\) là:

A. 0                            

B. 3                            

C. 1                            

D. 2

-----Còn tiếp-----

2.6. Đề thi giữa HK1 môn Toán 12 – Số 6

TRƯỜNG TRƯỜNG THPT NGUYỄN TRUNG THIÊN

ĐỀ THI GIỮA HK1

NĂM HỌC: 2021-2022

MÔN: TOÁN 12

Câu 1:  Cho hàm số y = f(x) có đạo hàm trên R và có bảng xét dấu f'(x) như sau:

Mệnh đề nào sau đây đúng?

A. Hàm số y = f(x) nghịch biến trên khoảng \((3\,;\, + \infty ).\)

B. Hàm số y = f(x) nghịch biến trên khoảng (-1; 3).

C. Hàm số y = f(x) đồng biến trên khoảng (-1; 2)

D. Hàm số y = f(x) đồng biến trên khoảng \(( - \infty \,;\,2).\)

Câu 2: Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như sau:

Mệnh đề nào sau đây đúng?

A. Hàm số y = f(x) có đúng một điểm cực trị.      

B. Hàm số y = f(x) đạt cực đại tại x = 2               

C. Hàm số y = f(x) đạt cực tiểu tại x = 2              

D. Hàm số y = f(x) đạt cực tiểu tại x = -1

Câu 3:  Đường tiệm cận đứng của đồ thị hàm số \(y = \frac{{2x - 1}}{{2 - 3x}}\) là đường thẳng

A. \(x = - \frac{2}{3}.\)

B. \(y = - \frac{2}{3}.\)

C. \(x = \frac{1}{2}.\)

D. \(x = \frac{2}{3}.\)

Câu 4: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?

A. \(y = - {x^3} + 3{x^2} - 1\).

B. \(y = - {x^3} + 3{x^2} + 1\).

C. \(y = {x^4} - 3{x^2} - 1\).

D. \(y = {x^3} - 3{x^2} - 1\).

Câu 5: Với a là số thực dương tùy ý, \({a^3}.{a^{\frac{1}{2}}}\) bằng

A. \({a^{\frac{3}{2}}}.\)

B. \({a^{\frac{9}{2}}}.\)

C. \({a^{\frac{7}{2}}}.\)

D. \({a^{\frac{5}{2}}}.\)

Câu 6:  Nếu \(x,\,\,y\) là hai số thực dương tùy ý thỏa mãn \(\ln x\le \ln y\) thì

A. \(x\le y.\)

B. \(x>y.\)                         

C. \(x

D. \(x\ge y.\)

-----Còn tiếp-----

Trường THPT Phan Châu Trinh

Số câu: 30 câu trắc nghiệm

Thời gian làm bài: 50 phút

Năm học: 2021 -2022

8. Đề thi giữa học kì 1 môn Toán 12 – Số 8

Trường THPT Trần Cao Vân

Số câu: 30 câu trắc nghiệm

Thời gian làm bài: 50 phút

Năm học: 2021 -2022   

9. Đề thi giữa học kì 1 môn Toán 12 – Số 9

Trường THPT Lê Quý Đôn

Số câu: 30 câu trắc nghiệm

Thời gian làm bài: 60 phút

Năm học: 2021 -2022    

10. Đề thi giữa học kì 1 môn Toán 12 – Số 10

Trường THPT Trường Chinh

Số câu: 30 câu trắc nghiệm

Thời gian làm bài: 50 phút

Năm học: 2021 -2022

---Bấm TẢI VỀ hoặc XEM ONLINE để xem đầy đủ nội dung các Đề thi 1-10---