Giải bài tập Giải SBT Vật Lí 9 Bài 5: Đoạn mạch song song
Nội dung hướng dẫn Giải bài tập SBT Lý 9 Bài 5 dưới đây sẽ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức về đoạn mạch song song. Mời các em cùng theo dõi.
Mục lục nội dung
1. Giải bài 5.1 trang 13 SBT Vật lý 9
2. Giải bài 5.2 trang 13 SBT Vật lý 9
3. Giải bài 5.3 trang 13 SBT Vật lý 9
4. Giải bài 5.4 trang 13 SBT Vật lý 9
5. Giải bài 5.5 trang 14 SBT Vật lý 9
6. Giải bài 5.6 trang 14 SBT Vật lý 9
7. Giải bài 5.7 trang 14 SBT Vật lý 9
8. Giải bài 5.8 trang 14 SBT Vật lý 9
9. Giải bài 5.9 trang 14 SBT Vật lý 9
10. Giải bài 5.10 trang 14 SBT Vật lý 9
11. Giải bài 5.11 trang 15 SBT Vật lý 9
12. Giải bài 5.12 trang 15 SBT Vật lý 9

1. Giải bài 5.1 trang 13 SBT Vật lý 9
Cho mạch điện có sơ đồ như hình 5.1, trong đó R1=15Ω, R2=10Ω, vôn kế chỉ 12V.
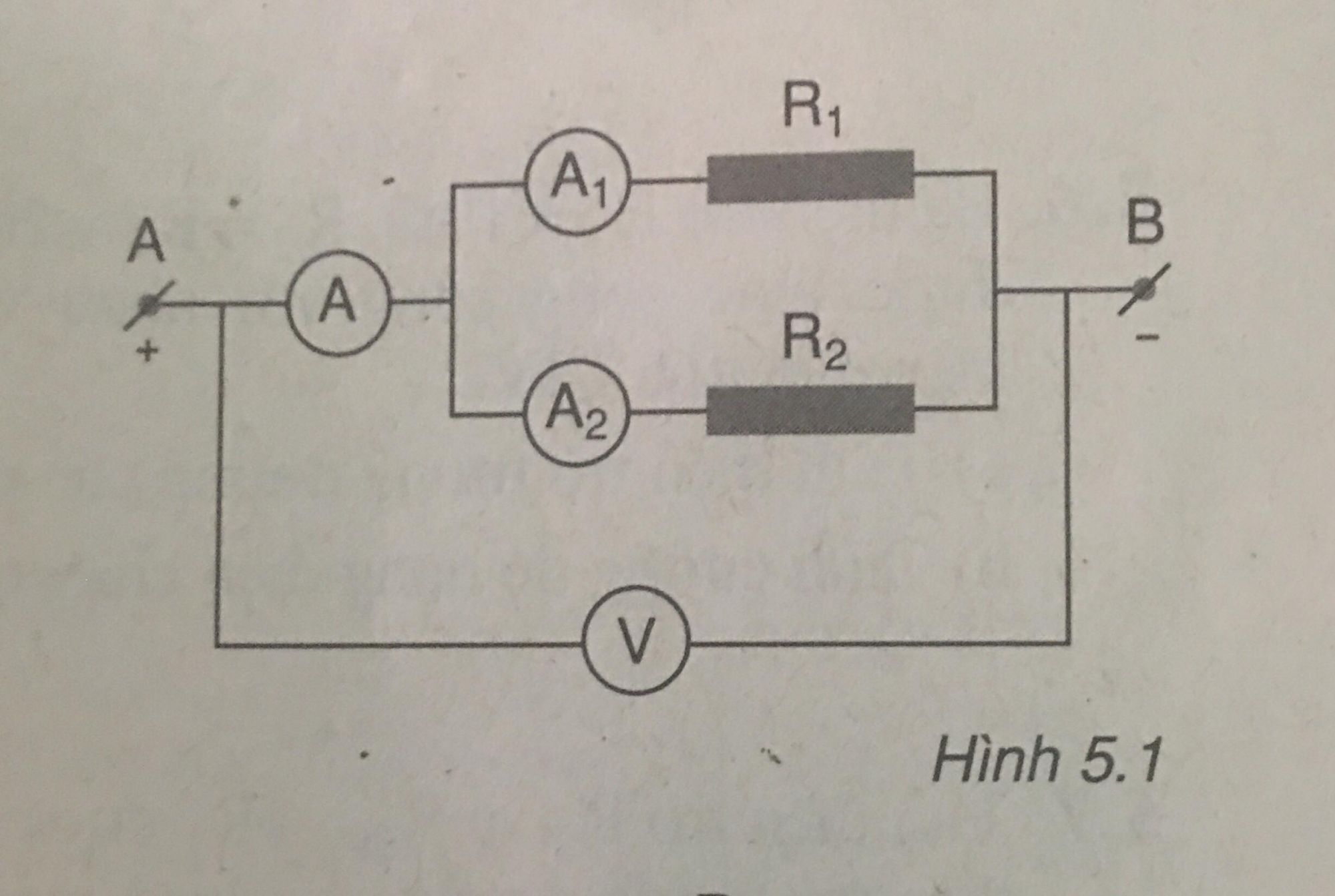
a. Tính điện trở tương đương của đoạn mạch.
b. Tính số chỉ của các ampe kế.
Phương pháp giải
a. Tính điện trở tương đương theo công thức:
\({R_{AB}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\)
b. Áp dụng công thức: I=U/R để tính số chỉ của các ampe kế
Hướng dẫn giải
a. Điện trở tương đương của đoạn mạch là:
\({R_{AB}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{15 \times 10}}{{15 + 10}} = 6{\rm{\Omega }}\)
b. Số chỉ của các ampe kế là:
\(\begin{array}{l} {I_{AB}} = \frac{U}{{{R_{AB}}}} = \frac{{12}}{6} = 2A\\ {I_1} = \frac{U}{{{R_1}}} = \frac{{12}}{{15}} = 0,8A\\ {I_2} = \frac{U}{{{R_2}}} = \frac{{12}}{{10}} = 1,2A \end{array}\)
Vậy ampe kế ở mạch chính chỉ 2A, ampe kế 1 chỉ 0,8A và ampe kế 2 chỉ 1,2A
2. Giải bài 5.2 trang 13 SBT Vật lý 9
Cho mạch điện có sơ đồ hình 5.2, trong đó R1=5Ω, R2=10Ω, ampe kế A1 chỉ 0,6A
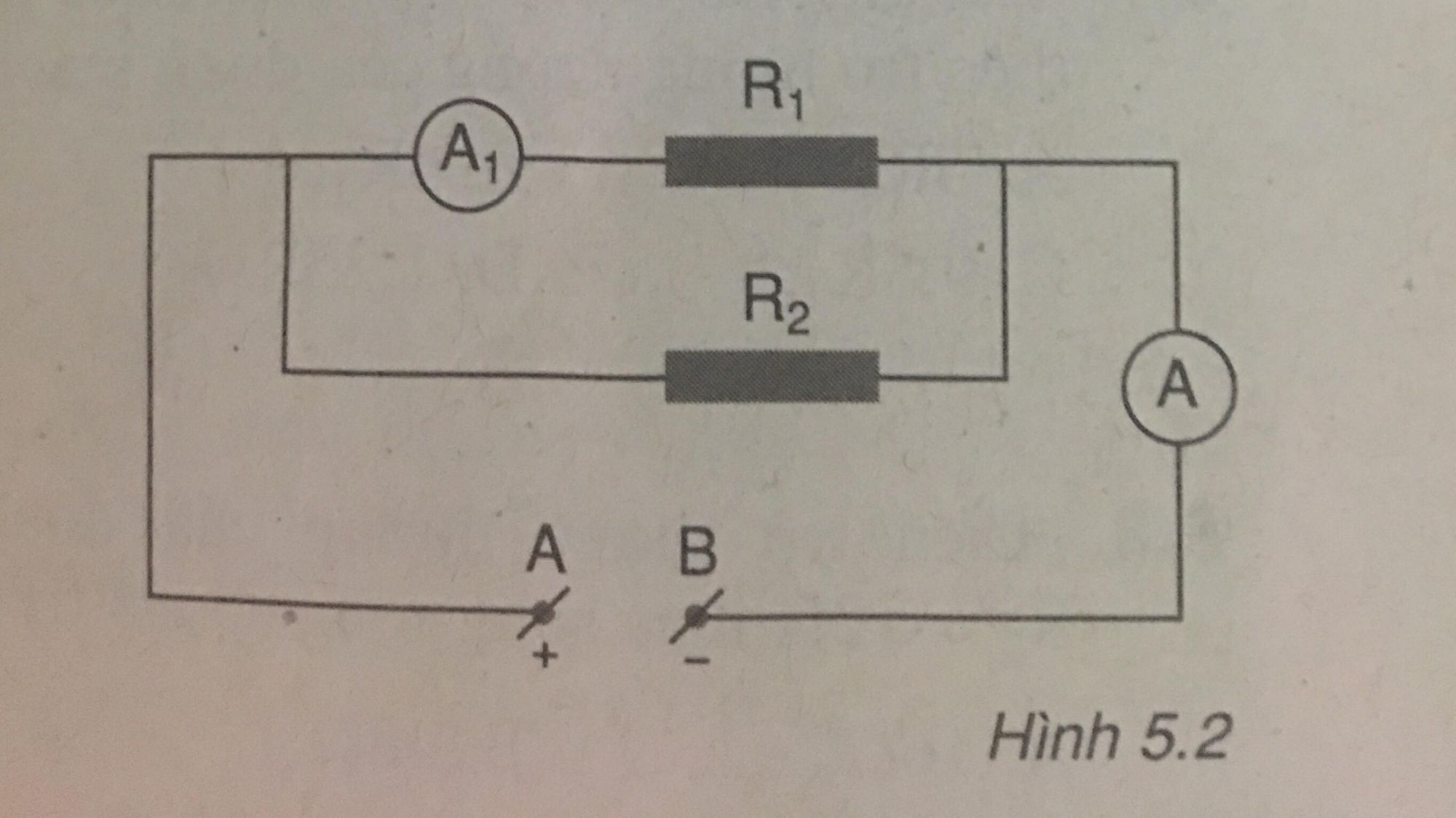
a. Tính hiệu điện thế giữa hai đầu AB của đoạn mạch.
b. Tính cường độ dòng điện ở mạch chính.
Phương pháp giải
a. Tính hiệu điện thế giữa hai đầu AB theo công thức:
\({U_{AB}} = {I_1}.{R_1} \)
b. Tính cường độ dòng điện ở mạch chính theo công thức:
\({I_{AB}} = \frac{{{U_{AB}}}}{{{R_{td}}}}\) với \({R_{td}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} \)
Hướng dẫn giải
a. Do hai điện trở mắc song song với nhau nên hiệu điện thế giữa hai đầu AB của đoạn mạch bằng hiệu điện thế giữa mỗi đầu đoạn mạch rẽ.
=> Hiệu điện thế giữa hai đầu AB của đoạn mạch là:
\({U_{AB}} = {I_1}.{R_1} = 0,6.5 = 3V\)
b. Mạch gồm R1 // R2
- Điện trở tương đương của mạch là:
\({R_{td}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{10.5}}{{10 + 5}} = \frac{{50}}{{15}} = \frac{{10}}{3}{\rm{\Omega }}\)
- Cường độ dòng điện ở mạch chính là:
\({I_{AB}} = \frac{{{U_{AB}}}}{{{R_{td}}}} = \frac{3}{{\frac{{10}}{3}}} = \frac{9}{{10}} = 0,9A\)
3. Giải bài 5.3 trang 13 SBT Vật lý 9
Cho mạch điện có sơ đồ hình 5.3, trong đó R1=20Ω, R2=30Ω, ampe kế chỉ 1,2A. Tính số chỉ của các ampe kế A1 và A2.
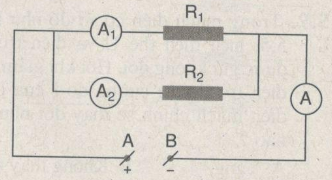
Phương pháp giải
- Tính điện trở tương đương theo công thức:
\({R_{AB}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} \)
- Số chỉ của các ampe kế tính theo công thức: I=U/R
Với \({U_{AB}} = {U_1} = {U_2}= I.{R_{AB}}\)
Hướng dẫn giải
Ta có: R1//R2
=> Điện trở tương đương của toàn mạch là:
\({R_{AB}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{20.30}}{{20 + 30}} = 12{\rm{\Omega }}\)
\({U_{AB}} = I.{R_{AB}} = 1,2.12 = 14,4V\)
- Do điện trở R1 mắc song song với R2 nên ta có:
\({U_{AB}} = {U_1} = {U_2}\)
- Số chỉ của ampe kế 1 là:
\({I_1} = \frac{{{U_1}}}{{{R_1}}} = \frac{{{U_{AB}}}}{{{R_1}}} = \frac{{14,4}}{{20}} = 0,72A\)
- Số chỉ của ampe kế 2 là:
\({I_2} = \frac{{{U_2}}}{{{R_1}}} = \frac{{{U_{AB}}}}{{{R_2}}} = \frac{{14,4}}{{30}} = 0,48A\)
4. Giải bài 5.4 trang 13 SBT Vật lý 9
Cho hai điện trở, R1=15Ω chịu được dòng điện có cường độ tối đa 2A và R2=10Ω chịu được dòng điện có cường độ tối đa 1A. Hiệu điện thế tối đa có thể đặt vào hai đầu đoạn mạch gồm R1 và R2 mắc song song là:
A. 40V B. 10V C. 30V D. 25V
Phương pháp giải
- Áp dụng công thức: U=I.R để tính hiệu điện thế tối đa đặt vào mỗi điện trở
- Hiệu điện thế tối đa có thể đặt vào hai đầu đoạn mạch được tính theo công thức:
U1max=U2max
Hướng dẫn giải
- Hiệu điện thế tối đa đặt vào hai đầu điện trở R1 là:
U1max=I1max.R1=2.15=30V
- Hiệu điện thế tối đa đặt vào hai đầu điện trở R2 là:
U2=I2max.R2=1.10=10V
- Vì R1 song song R2 nên hiệu điện thế giữa hai đầu các điện trở bằng nhau:
U=U1=U2=10V
- Vì vậy hiệu điện thế tối đa có thể đặt vào hai đầu đoạn mạch là:
U1max=U2max=10V
- Chọn đáp án B
5. Giải bài 5.5 trang 14 SBT Vật lý 9
Cho mạch điện có sơ đồ như hình 5.4, vôn kế chỉ 36V, ampe kế chỉ 3A, R1=30Ω.
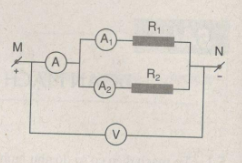
a. Tính điện trở R2.
b. Tính số chỉ của các ampe kế A1 và A2.
Phương pháp giải
a. Dựa vào công thức tính diền trở tương đương:
\({R_{td}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{U}{I}\) để tính R2
b. Áp dụng công thức: I=U/R để tính số chỉ của các ampe kế A1 và A2 với:
\(\begin{array}{l} U = {U_1} = {U_2}\\ I = {I_1} + {I_2} \end{array}\)
Hướng dẫn giải
a. R1//R2 nên ta có điện trở tương đương của mạch là:
\({R_{td}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\)
Mặt khác, ta có: Rtđ=U/I
Ta suy ra:
\({R_{td}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{U}{I} = \frac{{36}}{3} = 12{\rm{\Omega }}\)
Thay R1=30Ω ta được:
\(\begin{array}{*{20}{c}} {}&{\frac{{30.{R_2}}}{{30 + {R_2}}} = 12}\\ {}&{ \Rightarrow 30{R_2} = 12.\left( {30 + {R_2}} \right)}\\ {}&{ \Rightarrow 30{R_2} = 360 + 12{R_2}}\\ {}&{ \Rightarrow 30{R_2} - 12{R_2} = 360}\\ {}&{ \Rightarrow 18{R_2} = 360}\\ {}&{ \Rightarrow {R_2} = \frac{{360}}{{18}} = 20{\mkern 1mu} {\rm{\Omega }}} \end{array}\)
b. Do R1//R2 ta có:
\(\begin{array}{l} U = {U_1} = {U_2}\\ I = {I_1} + {I_2} \end{array}\)
Ta suy ra:
- Số chỉ của ampe kế 1 là:
\({I_1} = \frac{U}{{{R_1}}} = \frac{{36}}{{30}} = 1,2A\)
- Số chỉ của ampe kế 2 là:
I2=I−I1=3−1,2=1,8A
6. Giải bài 5.6 trang 14 SBT Vật lý 9
Ba điện trở R1=10Ω, R2=R3=20Ω được mắc song song với nhau vào hiệu điện thế 12V.
a. Tính điện trở tương đương của đoạn mạch.
b. Tính cường độ dòng điện chạy qua mạch chính và qua từng mạch rẽ.
Phương pháp giải
a. Áp dụng công thức:
\(\frac{1}{{{R_{td}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}}\) để tính điện trở tương đương
b. - Tính cường độ dòng điện chạy qua từng mạch rẽ theo công thức: I=U/R
- Áp dụng công thức: I=I1+I2+I3 để tính cường độ dòng điện chạy qua mạch chính
Hướng dẫn giải
a. Ta có: R1//R2//R3
Suy ra, điện trở tương đương của toàn mạch:
\(\begin{array}{*{20}{l}} \begin{array}{l} \frac{1}{{{R_{td}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}}\\ = \frac{1}{{10}} + \frac{1}{{20}} + \frac{1}{{20}} = \frac{1}{5} \end{array}\\ { \Rightarrow {R_{td}} = 5{\rm{\Omega }}} \end{array}\)
b. Do R1//R2//R3 nên ta có:
U=U1=U2=U3 và cường độ dòng điện I=I1+I2+I3
- Cường độ dòng điện chạy qua từng mạch rẽ là:
\(\begin{array}{l} {I_1} = \frac{U}{{{R_1}}} = \frac{{12}}{{10}} = 1,2A\\ {I_2} = {I_3} = \frac{U}{{{R_2}}} = \frac{{12}}{{20}} = 0,6A \end{array}\)
- Cường độ dòng điện qua mạch chính là:
\(I = {I_1} + {I_2} + {I_3} = 1,2 + 0,6 + 0,6 = 2,4A\)
7. Giải bài 5.7 trang 14 SBT Vật lý 9
Hai điện trở R1 và R2=4R1 được mắc song song với nhau. Khi tính theo R1 thì điện trở tương đương của đoạn mạch này có kết quả nào dưới đây?
A. 5R1 B. 4R1 C. 0,8R1 D. 1,25R1
Phương pháp giải
Áp dụng công thức:
\({R_{td}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\) để tính điện trở tương đương
Hướng dẫn giải
Mạch gồm R1// R2
- Điện trở tương đương của đoạn mạch là:
\(\begin{array}{l} {R_{td}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\\ = \frac{{{R_1}.4{R_1}}}{{{R_1} + 4{R_1}}} = \frac{{4{R_1}.{R_1}}}{{5{R_1}}} = 0,8{R_1} \end{array}\)
- Chọn đáp án C.
8. Giải bài 5.8 trang 14 SBT Vật lý 9
Điện trở tương đương của đoạn mạch gồm hai điện trở R1=4Ω và R2=12Ω mắc song song có giá trị nào dưới đây?
A.16Ω B.48Ω C.0,33Ω D.3Ω
Phương pháp giải
Áp dụng công thức:
\({R_{td}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\) để tính điện trở tương đương
Hướng dẫn giải
- Điện trở tương đương của đoạn mạch là:
\({R_{td}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{4.12}}{{4 + 12}} = 3{\rm{\Omega }}\)
- Chọn đáp án D
9. Giải bài 5.9 trang 14 SBT Vật lý 9
Trong mạch điện có sơ đồ như hình 5.5, hiệu điện thế U và điện trở R1 được giữ không đổi. Hỏi khi giảm dần điện trở R2 thì cường độ I của mạch điện chính sẽ thay đổi như thế nào?
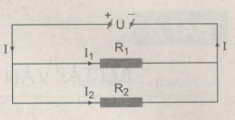
A. Tăng. B. Không thay đổi.
C. Giảm. D. Lúc đầu tăng, sau đó giảm.
Phương pháp giải
- Tính hiệu điện thế và cường độ của mạch chính theo công thức:
U1=U2=U và I=I1+I2
- Áp dụng công thức: I=U/R để tính cường độ qua từng điện trở
- Dựa vào công thức:
\(I = {I_1} + {I_2} = \frac{U}{{{R_1}}} + \frac{U}{{{R_2}}}\) để tìm sự thay đổi của I khi thay đổi R2
Hướng dẫn giải
- Ta có, mạch gồm R1//R2, khi đó:
+ Hiệu điện thế trên toàn mạch bằng hiệu điện thế trên các mạch nhánh:
U1=U2=U
+ Cường độ dòng điện trong mạch chính: I=I1+I2
Lại có:
+ Cường độ dòng điện qua điện trở R1:
\({I_1} = \frac{{{U_1}}}{{{R_1}}} = \frac{U}{{{R_1}}}\)
+ Cường độ dòng điện qua điện trở R2:
\({I_2} = \frac{{{U_2}}}{{{R_2}}} = \frac{U}{{{R_2}}}\)
Suy ra cường độ dòng điện của mạch chính:
\(I = {I_1} + {I_2} = \frac{U}{{{R_1}}} + \frac{U}{{{R_2}}}\)
Theo đầu bài, U và R1 không đổi
=> Nếu R2 giảm thì U2 tăng=> I tăng
- Chọn đáp án A
10. Giải bài 5.10 trang 14 SBT Vật lý 9
Ba điện trở R1=5Ω, R2=10Ω và R3=30Ω được mắc song song với nhau. Điện trở tương đương của đoạn mạch song song này là bao nhiêu?
A. 0,33Ω B. 3Ω C. 33,3Ω D. 45Ω
Phương pháp giải
Áp dụng công thức:
\(\begin{array}{*{20}{l}} {\frac{1}{{{R_{td}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}}}\\ \end{array}\) để tính điện trở tương đương
Hướng dẫn giải
- Điện trở tương đương của mạch:
\(\begin{array}{*{20}{l}} {\frac{1}{{{R_{td}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}}}\\ { = \frac{1}{5} + \frac{1}{{10}} + \frac{1}{{30}} = \frac{1}{3}}\\ { \Rightarrow {R_{td}} = 3{\rm{\Omega }}} \end{array}\)
Vậy điện trở tương đương của đoạn mạch là 3Ω
- Chọn đáp án: B
11. Giải bài 5.11 trang 15 SBT Vật lý 9
Cho mạch điện có sơ đồ như hình 5.6, trong đó điện trở R1=6Ω; dòng điện mạch chính có cường độ I=1,2A và dòng điện đi qua điện trở R2 có cường độ I2=0,4A.
.png)
a. Tính R2
b. Tính hiệu điện thế U đặt vào hai đầu đoạn mạch.
c. Mắc một điện trở R3 vào mạch điện trên , song song với R1 và R2 thì dòng điện trong mạch chính có cường độ là 1,5A. Tính R3 và điện trở tương đương Rtđ của đoạn mạch này khi đó.
Phương pháp giải
a) - Tính hiệu điện thế và cường độ toàn mạch theo công thức:
U=U1=U2 và I=I1+I2
- Lập tỉ số giữa cường độ qua hai điện trở:
\({\frac{{{I_1}}}{{{I_2}}} = \frac{{{R_2}}}{{{R_1}}}}\) để tìm R2
b) Áp dụng công thức:
U=U1=U2=I1.R1 để tính hiệu điện thế toàn mạch
c) - Điện trở tương đương của mạch được tính theo công thức:
Rtd=U/I
- Tính điện trở tương đương của mạch qua điện trở 1 và 2:
\({R_{12}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} \)
- Dựa vào công thức tính điện trở toàn mạch:
\(\begin{array}{*{20}{c}} {}&{\frac{1}{{{R_{td}}}} = \frac{1}{{{R_3}}} + \frac{1}{{{R_{12}}}}}\\ \end{array}\) để tính R3
Hướng dẫn giải
a) Mạch gồm R1//R2, nên ta có:
- Hiệu điện thế qua R1 bằng hiệu điện thế qua R2 và bằng hiệu điện thế của toàn mạch:
U=U1=U2
- Cường độ dòng điện trong mạch: I=I1+I2
Ta suy ra, cường độ dòng điện qua điện trở R1 là:
\({I_1} = I - {I_2} = 1,2 - 0,4 = 0,8{\rm{A}}\)
Lại có:
\(\begin{array}{l} {I_1} = \frac{{{U_1}}}{{{R_1}}} = \frac{U}{{{R_1}}} = 0,8A(1)\\ {I_2} = \frac{{{U_2}}}{{{R_2}}} = \frac{U}{{{R_2}}} = 0,4A(2) \end{array}\)
Lấy (1)/(2) ta được:
\(\begin{array}{*{20}{l}} {\frac{{{I_1}}}{{{I_2}}} = \frac{{\frac{U}{{{R_1}}}}}{{\frac{U}{{{R_2}}}}} = \frac{{{R_2}}}{{{R_1}}} = \frac{{0,8}}{{0,4}} = 2}\\ { \Rightarrow {R_2} = 2{R_1} = 2.6 = 12{\rm{\Omega }}} \end{array}\)
b) Ta có: U=U1=U2
Hiệu diện thế qua điện trở R1 là:
U1=I1.R1=0,8.6=4,8V
⇒U=U1=U2=4,8V
Vậy hiệu điện thế đặt vào hai đầu đoạn mạch là: U=4,8V
c) Điện trở tương đương của mạch là:
\({R_{td}} = \frac{U}{I} = \frac{{4,8}}{{1,5}} = 3,2{\rm{\Omega }}\)
- Điện trở tương đương của điện trở R1 và R2 là R12
\({R_{12}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{6.12}}{{6 + 12}} = 4{\rm{\Omega }}\)
Lại có: R12//R3
- Ta có:
\(\begin{array}{*{20}{c}} {}&{\frac{1}{{{R_{td}}}} = \frac{1}{{{R_3}}} + \frac{1}{{{R_{12}}}}}\\ {}&{ \Rightarrow \frac{1}{{{R_3}}} = \frac{1}{{{R_{td}}}} - \frac{1}{{{R_{12}}}}}\\ {}&{ \Rightarrow \frac{1}{{{R_3}}} = \frac{1}{{3,2}} - \frac{1}{4} = \frac{1}{{16}}}\\ {}&{ \Rightarrow {R_3} = 16{\rm{\Omega }}} \end{array}\)
Vậy điện trở R3=16Ω và điện trở tương đương của đoạn mạch là Rtđ=3,2Ω
12. Giải bài 5.12 trang 15 SBT Vật lý 9
Cho một ampe kế, một hiệu điện thế U không đổi, các dây dẫn nối, một điện trở R đã biết giá trị và một điện trở Rx chưa biết giá trị. Hãy nêu một phương án giúp xác định giá trị của Rx (Vẽ hình và giải thích cách làm)
Phương pháp giải
Vận dụng kiến thức về đoạn mạch song song để trả lời câu hỏi này
Hướng dẫn giải
- Hình vẽ: Vẽ mạch điện gồm ampe kế, điện trở R và biến trở Rx như hình dưới đây:
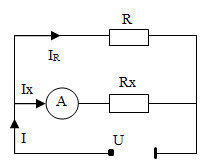
- Cách làm: Dùng ampe kế đo cường độ dòng điện qua mạch, ta sẽ có cường độ dòng điện qua R và Rx. Áp dụng công thức tính R=U/I ta tính được Rtđ và Rx
13. Giải bài 5.13 trang 15 SBT Vật lý 9
Cho một hiệu điện thế U = 1,8V và hai điện trở R1, R2. Nếu mắc nối tiếp hai điện trở này vào hiệu điện thế U thì dòng điện đi qua chúng có cường độ I1 = 0,2A; nếu mắc song song hai điện trở này vào hiệu điện thế U thì dòng điện mạch chính có cường độ I2 = 0,9A. Tính R1, R2?
Phương pháp giải
- Tính điện trở của đoạn mạch nối tiếp theo công thức:
\(R = {R_1} + {R_2} = \frac{U}{{{I_1}}} \)
- Tính điện trở của đoạn mạch song song theo công thức:
\({R_{td}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{U}{{{I_2}}} \)
- Lập tỉ số giữa R1/R2 để tìm giá trị R1
Hướng dẫn giải
- R1 mắc nối tiếp R2:
\(R = {R_1} + {R_2} = \frac{U}{{{I_1}}} = \frac{{1,8}}{{0,2}} = 9{\rm{\Omega (1)}}\)
- R1 mắc song song:
\({R_{td}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{U}{{{I_2}}} = \frac{{1,8}}{{0,9}} = 2{\rm{\Omega (2)}}\)
Từ (1) và (2) ta được:
\(\Rightarrow {R_1}.{R_2} = 18 \Rightarrow {R_1} = \frac{{18}}{{{R_2}}}(3)\)
Thay (3) vào (1), ta được:
\(\begin{array}{l} {R_2} = 6{\mkern 1mu} {\mkern 1mu} {\rm{\Omega }} \Rightarrow {R_1} = 3{\mkern 1mu} {\mkern 1mu} {\rm{\Omega }}\\ {R_2} = 3{\mkern 1mu} {\mkern 1mu} {\rm{\Omega }} \Rightarrow {R_1} = 6{\mkern 1mu} {\mkern 1mu} {\rm{\Omega }} \end{array}\)
14. Giải bài 5.14 trang 15 SBT Vật lý 9
Một đoạn mạch gồm 3 điện trở R1 =9Ω, R2 =18Ω và R3 =24Ω được mắc vào hiệu điện thế U = 3,6V như sơ đồ trên hình 5.7.
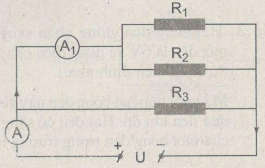
a. Tính điện trở tương đương của đoạn mạch.
b. Tính số chỉ I của ampe kế A và số chỉ I12 của ampe kế A1.
Phương pháp giải
a) Tính điện trở tương đương theo công thức:
\(\begin{array}{l} \frac{1}{{{R_{td}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}}\\\end{array}\)
b) Tính số chỉ ampe kế theo công thức:
\({I_{12}} = \frac{U}{{{R_{12}}}}\) với
\(\frac{1}{{{R_{12}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\)
Hướng dẫn giải
a) Điện trở tương đương của đoạn mạch:
\(\begin{array}{l} \frac{1}{{{R_{td}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}}\\ \Rightarrow \frac{1}{{{R_{td}}}} = \frac{1}{9} + \frac{1}{{18}} + \frac{1}{{24}}\\ \Rightarrow {R_{td}} = 4,8{\rm{\Omega }} \end{array}\)
b) Số chỉ của ampe kế:
\(\begin{array}{l} - \,\,\,I = \frac{U}{{{R_{td}}}} = \frac{{3,6}}{{4,8}} = 0,75A\\ - \,\,\,\frac{1}{{{R_{12}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} = \frac{1}{9} + \frac{1}{{18}}\\ \Rightarrow {R_{12}} = 6{\rm{\Omega }}\\ - \,\,\,{I_{12}} = \frac{U}{{{R_{12}}}} = \frac{{3,6}}{6} = 0,6A \end{array}\)
Vậy số chỉ của ampe kế A là 0,75A; số chỉ của ampe kế A1 là 0,6A
Tham khảo thêm
- doc Giải bài tập Giải SBT Vật Lí 9 Bài 1: Sự phụ thuộc của cường độ dòng điện vào hiệu điện thế giữa hai đầu dây dẫn
- doc Giải bài tập Giải SBT Vật Lí 9 Bài 2: Điện trở của dây dẫn - Định luật Ôm
- doc Giải bài tập Giải SBT Vật Lí 9 Bài 4: Đoạn mạch nối tiếp
- doc Giải bài tập SBT Vật Lí 9 Bài 6: Bài tập vận dụng định luật Ôm
- doc Giải bài tập SBT Vật Lí 9 Bài 7: Sự phụ thuộc của điện trở vào chiều dài dây dẫn
- doc Giải bài tập Giải SBT Vật Lí 9 Bài 8: Sự phụ thuộc của điện trở vào tiết diện dây dẫn
- doc Giải bài tập Giải SBT Vật Lí 9 Bài 9: Sự phụ thuộc của điện trở vào vật liệu làm dây dẫn
- doc Giải bài tập SBT Vật Lí 9 Bài 10: Biến trở - Điện trở dùng trong kĩ thuật
- doc Giải bài tập SBT Vật Lí 9 Bài 11: Bài tập vận dụng định luật Ôm và công thức tính điện trở của dây dẫn
- doc Giải bài tập SBT Vật Lí 9 Bài 12: Công suất điện
- doc Giải bài tập SBT Vật Lí 9 Bài 13: Điện năng - Công của dòng điện
- doc Giải bài tập SBT Vật Lí 9 Bài 14: Bài tập về công suất điện và điện năng sử dụng
- doc Giải bài tập SBT Vật Lí 9 Bài 16 - 17: Định luật Jun - Len-xơ. Bài tập vận dụng định luật Jun - Len-xơ
- doc Giải bài tập SBT Vật Lí 9 Bài 19: Sử dụng an toàn và tiết kiệm điện
