Giải bài tập SBT Toán 10 Bài 4: Các tập hợp số
eLib xin giới thiệu đến quý thầy cô giáo và các em học sinh nội dung giải bài tập bài Các tập hợp số trang 16 SBT Toán 10 bên dưới đây. Thông qua tài liệu này các em vừa ôn tập được kiến thức vừa nâng cao kĩ năng làm bài hiệu quả để từ đó có phương pháp học tập phù hợp. Mời các em cùng tham khảo.
Mục lục nội dung

1. Giải bài 1.31 trang 16 SBT Đại số 10
Xác định mỗi tập hợp sau và biểu diễn nó trên trục số
a) (-3; 3) ∪ (-1; 0)
b) (-1; 3) ∪ [0; 5]
c) (-∞; 0) ∩ (0; 1)
d) (-2; 2] ∩ [1; 3)
Phương pháp giải
Bước 1: Biểu diễn các tập hợp số trên trục số
Bước 2: Sử dụng kiến thức về các phép toán tập hợp.
- Giao của hai tập hợp A và B, kí hiệu A ∩ B là tập hợp gồm các phần tử vừa thuộc A vừa thuộc B
- Hợp của hai tập hợp A và B, kí hiệu A ∪ B là tập hợp gồm các phần tử thuộc A hoặc thuộc B
- Hiệu của tập hợp A với tập hợp B, kí hiệu \(A\backslash B\) là tập hợp gồm các phần tử thuộc A và không thuộc B
- Nếu B ⊂ A thì \(A\backslash B\) được gọi là phần bù của B trong A, kí hiệu là \({C_A}B\)
Hướng dẫn giải
a)
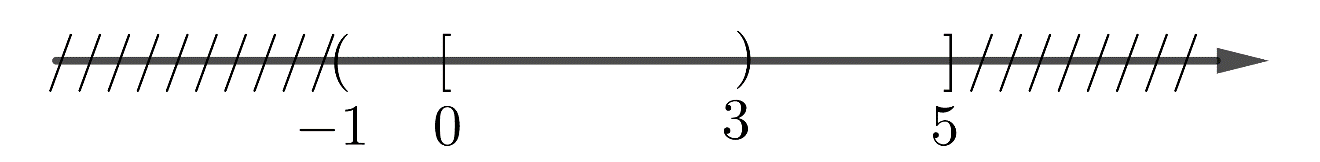
\(( - 1;3) \cup {\rm{[0}};5{\rm{] = ( - 1;5]}}\)
b)
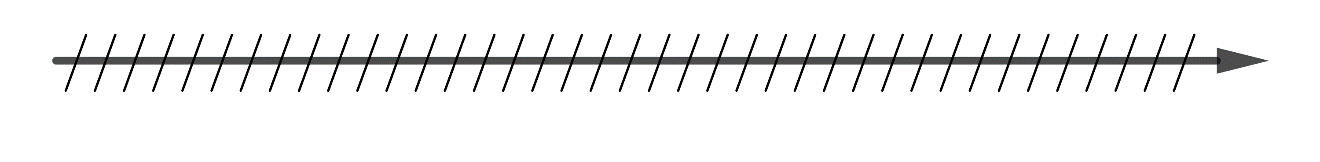
\(( - \infty ;0) \cap (0;1) =\emptyset \)
c)
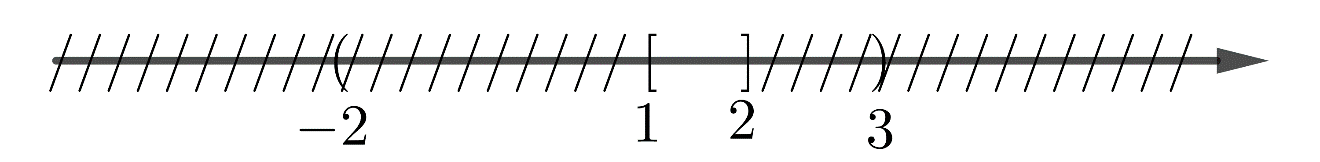
\(( - 2;2{\rm{]}} \cap {\rm{[}}1;3) = {\rm{[}}1;2]\)
2. Giải bài 1.32 trang 16 SBT Đại số 10
Xác định tập hợp A ∩ B, với
a) A = [1;5]; B = (-3;2) ∪ (3;7)
b) A = (-5;0) ∪ (3;5) ; B = (-1;2) ∪ [1;3]
Phương pháp giải
Bước 1: Biểu diễn các tập hợp số trên trục số
Bước 2: Sử dụng kiến thức về các phép toán tập hợp.
- Giao của hai tập hợp A và B, kí hiệu A ∩ B là tập hợp gồm các phần tử vừa thuộc A vừa thuộc B
- Hợp của hai tập hợp A và B, kí hiệu A ∪ B là tập hợp gồm các phần tử thuộc A hoặc thuộc B
- Hiệu của tập hợp A với tập hợp B, kí hiệu \(A\backslash B\) là tập hợp gồm các phần tử thuộc A và không thuộc B
- Nếu B ⊂ A thì \(A\backslash B\) được gọi là phần bù của B trong A, kí hiệu là \({C_A}B\)
Hướng dẫn giải
a)

\(A \cap B = {\rm{[}}1;2) \cup (3;5]\)
b)
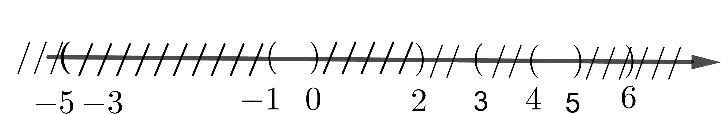
\(A \cap B = ( - 1;0) \cup (4;5)\)
3. Giải bài 1.33 trang 16 SBT Đại số 10
Xác định tính đúng, sai của mỗi mệnh đề sau
a) [-3; 0] ∩ (0; 5) = {0}
b) (-∞; 2) ∪ (2; +∞) = (-∞; +∞)
c) (-1; 3) ∩ (2; 5) = (2; 3)
d) (1; 2) ∪ (2; 5) = (1; 5)
Phương pháp giải
Bước 1: Biểu diễn các tập hợp số trên trục số
Bước 2: Sử dụng kiến thức về các phép toán tập hợp.
- Giao của hai tập hợp A và B, kí hiệu A ∩ B là tập hợp gồm các phần tử vừa thuộc A vừa thuộc B
- Hợp của hai tập hợp A và B, kí hiệu A ∪ B là tập hợp gồm các phần tử thuộc A hoặc thuộc B
- Hiệu của tập hợp A với tập hợp B, kí hiệu \(A\backslash B\) là tập hợp gồm các phần tử thuộc A và không thuộc B
- Nếu B ⊂ A thì \(A\backslash B\) được gọi là phần bù của B trong A, kí hiệu là \({C_A}B\)
Hướng dẫn giải
a) Sai vì
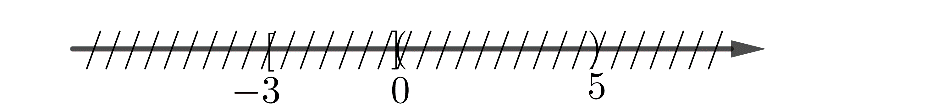
Vậy \({\rm{[-3;0]}} \cap {\rm{ (0;5)}} = \emptyset\)
b) Sai vì \(( - \infty ;2) \cup (2; + \infty ) = ( - \infty ; + \infty )\backslash \left\{ 2 \right\}\)
c) Đúng
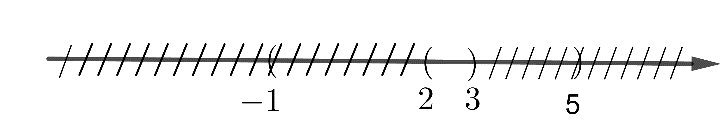
d) Sai vì

Vậy \((1;2) \cup (2;5) = (1;5)\backslash \left\{ 2 \right\}\)
4. Giải bài 1.34 trang 16 SBT Đại số 10
Cho a, b, c, d là những số thực và a < b < c < d. Xác định các tập hợp số sau:
a) (a; b) ∩ (c; d)
b) (a; c] ∩ [b; d)
c) (a; d) \ (b; c)
d) (b; d) \ (a; c)
Phương pháp giải
Bước 1: Biểu diễn các tập hợp số trên trục số
Bước 2: Sử dụng kiến thức về các phép toán tập hợp.
- Giao của hai tập hợp A và B, kí hiệu A ∩ B là tập hợp gồm các phần tử vừa thuộc A vừa thuộc B
- Hợp của hai tập hợp A và B, kí hiệu A ∪ B là tập hợp gồm các phần tử thuộc A hoặc thuộc B
- Hiệu của tập hợp A với tập hợp B, kí hiệu \(A\backslash B\) là tập hợp gồm các phần tử thuộc A và không thuộc B
- Nếu B ⊂ A thì \(A\backslash B\) được gọi là phần bù của B trong A, kí hiệu là \({C_A}B\)
Hướng dẫn giải
a)
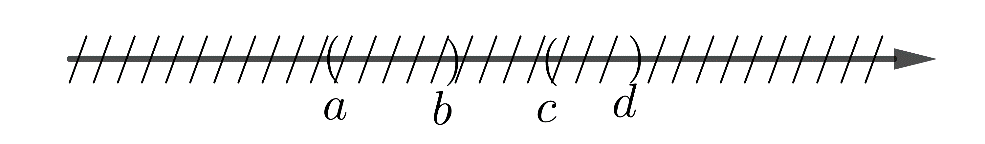
Vậy: (a; b) ∩ (c; d) = ∅
b)

Vậy: (a; c] ∩ [b; d) = [b; c]
c)
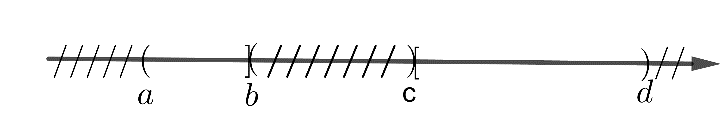
Vậy: (a; d) \ (b; c) = (a; b] ∪ [c; d]
d)
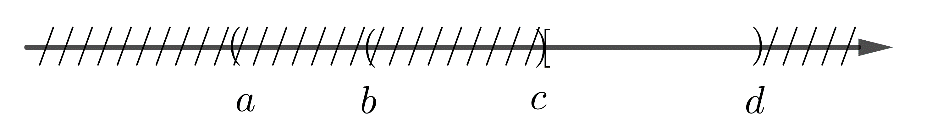
Vậy: (b; d) \ (a; c) = [c; d)
5. Giải bài 1.35 trang 16 SBT Đại số 10
Cho a ∈ R. Tìm mệnh đề đúng trong các mệnh đề sau:
A. R \ (-∞; a) = (a; +∞)
B. (-∞; a) ∩ (a; +∞) = {a}
C. R \ (a; +∞) = (-∞; a]
D. (-∞; a) ∪ (a; +∞) = R
Phương pháp giải
Sử dụng kiến thức về các phép toán tập hợp.
- Giao của hai tập hợp A và B, kí hiệu A ∩ B là tập hợp gồm các phần tử vừa thuộc A vừa thuộc B
- Hợp của hai tập hợp A và B, kí hiệu A ∪ B là tập hợp gồm các phần tử thuộc A hoặc thuộc B
- Hiệu của tập hợp A với tập hợp B, kí hiệu \(A\backslash B\) là tập hợp gồm các phần tử thuộc A và không thuộc B
- Nếu B ⊂ A thì \(A\backslash B\) được gọi là phần bù của B trong A, kí hiệu là \({C_A}B\)
Hướng dẫn giải
Đáp án A sai vì \(\mathbb{R}\backslash \left( { - \infty ;a} \right) = \left[ {a; + \infty } \right)\)
Đáp án B sai vì \(\left( { - \infty ;a} \right) \cap \left( {a; + \infty } \right) = \emptyset\)
Đáp án D sai vì \(\left( { - \infty ;a} \right) \cup \left( {a; + \infty } \right) = \mathbb{R}\backslash \left\{ a \right\}\)
Đáp án đúng: C
6. Giải bài 1.36 trang 16 SBT Đại số 10
Cho a, b ∈ R. Tìm mệnh đề đúng trong các mệnh đề sau:
A. (-∞; b) ∩ (a; +∞) = [a; b]
B. (-∞; b) ∩ (a; +∞) = (a; b)
C. (-∞; a) ∩ (-∞; b) = (a; b)
D. (-∞; b) ∩ (a; +∞] = (a; b)
Phương pháp giải
Sử dụng kiến thức về các phép toán tập hợp.
- Giao của hai tập hợp A và B, kí hiệu A ∩ B là tập hợp gồm các phần tử vừa thuộc A vừa thuộc B
- Hợp của hai tập hợp A và B, kí hiệu A ∪ B là tập hợp gồm các phần tử thuộc A hoặc thuộc B
- Hiệu của tập hợp A với tập hợp B, kí hiệu \(A\backslash B\) là tập hợp gồm các phần tử thuộc A và không thuộc B
- Nếu B ⊂ A thì \(A\backslash B\) được gọi là phần bù của B trong A, kí hiệu là \({C_A}B\)
Hướng dẫn giải
Đáp án A sai vì \(\left( { - \infty ;b} \right) \cap \left( {a; + \infty } \right) = \left( {a;b} \right)\)
Đáp án C sai vì \(\left( { - \infty ;a} \right) \cap \left( { - \infty ;b} \right) = \left( { - \infty ;a} \right)\)
Đáp án D sai vì \(\left( { - \infty ;b} \right) \cap \left[ {a; + \infty } \right) = \left[ {a;b} \right)\)
Đáp án đúng: B
Các em hãy luyện tập bài trắc nghiệm Các tập hợp số Toán 10 sau để nắm rõ thêm kiến thức bài học.
