Giải bài tập SBT Toán 10 Bài 1: Các định nghĩa
Dưới đây là hướng dẫn giải bài tập SBT Toán 10 Bài Các định nghĩa trang 10 với nội dung gồm 7 bài tập có hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. eLib hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.
Mục lục nội dung

1. Giải bài 1.1 trang 10 SBT Hình học 10
Hãy tính số các vec tơ (khác \(\overrightarrow 0\)) mà các điểm đầu và điểm cuối được lấy từ các điểm phân biệt đã cho trong các trường hợp sau:
a) Hai điểm
b) Ba điểm
c) Bốn điểm
Phương pháp giải
Liệt kê các véc tơ có thể có được từ các điểm đã cho và kết luận.
Hướng dẫn giải
a) Với hai điểm A, B có hai vec tơ \(\overrightarrow {AB} ,\overrightarrow {BA}\)
b) Với ba điểm A, B, C có 6 vec tơ \(\overrightarrow {AB} ,\overrightarrow {BA} ,\overrightarrow {AC} ,\overrightarrow {CA} ,\overrightarrow {BC} ,\overrightarrow {CB}\)
c) Với bốn điểm A, B, C, D có 12 véc tơ là:
\(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {BA} ,\overrightarrow {BC} ,\overrightarrow {BD} ,\overrightarrow {CA} ,\overrightarrow {CB} ,\overrightarrow {CD} ,\overrightarrow {DA} ,\overrightarrow {DB} ,\overrightarrow {DC} \)
2. Giải bài 1.2 trang 10 SBT Hình học 10
Cho hình vuông ABCD có tâm O. Liệt kê tất cả các vec tơ bằng nhau (khác \(\overrightarrow 0\)) nhận đỉnh và tâm của hình vuông làm điểm đầu và điểm cuối.
Phương pháp giải
Hai véc tơ bằng nhau nếu chúng có cùng hướng và độ lớn.
Hướng dẫn giải
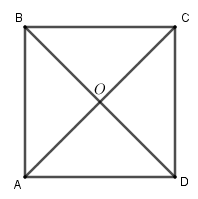
Ta thấy:
\(\overrightarrow {BC} = \overrightarrow {AD} ,\overrightarrow {CB} = \overrightarrow {DA}\)
\(\overrightarrow {AB} = \overrightarrow {DC} ,\overrightarrow {BA} = \overrightarrow {CD}\)
\(\overrightarrow {OB} = \overrightarrow {DO} ,\overrightarrow {BO} = \overrightarrow {OD}\)
\(\overrightarrow {AO} = \overrightarrow {OC} ,\overrightarrow {CO} = \overrightarrow {OA}\)
3. Giải bài 1.3 trang 10 SBT Hình học 10
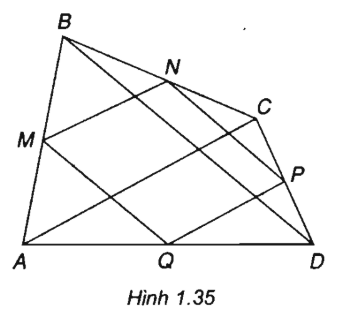
Cho tứ giác ABCD. Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA. Chứng minh \(\overrightarrow {NP} = \overrightarrow {MQ}\) và \(\overrightarrow {PQ} = \overrightarrow {NM}\)
Phương pháp giải
Chứng minh MNPQ là hình bình hành, từ đó suy ra điều phải chứng minh.
Hướng dẫn giải
Ta thấy, MN là đường trung bình của tam giác ABC nên MN//AC và \(MN = \dfrac{1}{2}AC\)
\(PQ\) là đường trung bình của tam giác ADC nên PQ//AC và \(PQ = \dfrac{1}{2}AC\)
Do đó NM//PQ và MN = PQ
Vậy tứ giác MNPQ là hình bình hành nên \(\overrightarrow {NP} = \overrightarrow {MQ} ,\overrightarrow {PQ} = \overrightarrow {NM}\)
4. Giải bài 1.4 trang 10 SBT Hình học 10
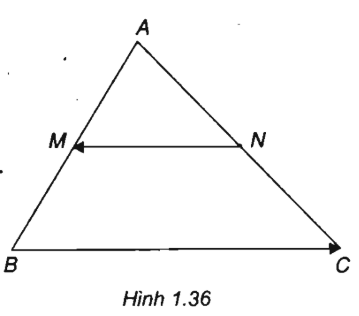
Cho tam giác ABC. Các điểm M và N lần lượt là trung điểm của các cạnh AB và AC. So sánh độ dài của hai vec tơ \(\overrightarrow {NM}\) và \(\overrightarrow {BC}\). Vì sao có thể nói hai vec tơ này cùng phương?
Phương pháp giải
Nhận xét các đoạn thẳng MN,BC dựa vào kiến thức đã biết, từ đó suy ra kết luận.
Hướng dẫn giải
Vì MN là đường trung bình của \(\Delta ABC\) nên MN//BC và \(MN = \dfrac{1}{2}BC\), hay \(\left| {\overrightarrow {MN} } \right| = \dfrac{1}{2}\left| {\overrightarrow {BC} } \right|\)
Vì MN//BC nên \(\overrightarrow {NM}\) và \(\overrightarrow {BC}\) cùng phương.
5. Giải bài 1.5 trang 10 SBT Hình học 10
Cho tứ giác ABCD, chứng minh rằng \(\overrightarrow {AB} = \overrightarrow {DC}\) thì \(\overrightarrow {AD} = \overrightarrow {BC}\)
Phương pháp giải
Nhận xét tính chất của tứ giác ABCD và từ đó suy ra kết luận.
Hướng dẫn giải
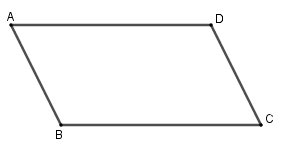
Tứ giác ABCD có \(\overrightarrow {AB} = \overrightarrow {DC}\) nên AB = DC và AB//DC. Do đó ABCD là hình bình hành, suy ra \(\overrightarrow {AD} = \overrightarrow {BC}\)
6. Giải bài 1.6 trang 10 SBT Hình học 10
Xác định vị trí tương đối của ba điểm phân biệt A,B và C. Trong các trường hợp sau:
a) \(\overrightarrow {AB}\) và \(\overrightarrow {AC}\) cùng hướng, \(\left| {\overrightarrow {AB} } \right| > \left| {\overrightarrow {AC} } \right|\)
b) \(\overrightarrow {AB} \) và \(\overrightarrow {AC}\) ngược hướng;
c) \(\overrightarrow {AB}\) và \(\overrightarrow {AC}\) cùng phương.
Phương pháp giải
Dựng hình và nhận xét.
Hướng dẫn giải
a) Nếu \(\overrightarrow {AB}\) và \(\overrightarrow {AC}\) cùng hướng, \(\left| {\overrightarrow {AB} } \right| > \left| {\overrightarrow {AC} } \right|\) thì điểm C nằm giữa hai điểm A và B.

b) Nếu \(\overrightarrow {AB}\) và \(\overrightarrow {AC}\) ngược hướng thì điểm A nằm giữa hai điểm B và C.

c) Nếu \(\overrightarrow {AB}\) và \(\overrightarrow {AC}\) cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
Trường hợp \(\overrightarrow {AB}\) và \(\overrightarrow {AC}\) cùng hướng:
-Nếu \(\left| {\overrightarrow {AB} } \right| > \left| {\overrightarrow {AC} } \right|\) thì C nằm giữa A và B.
-Nếu \(\left| {\overrightarrow {AB} } \right| < \left| {\overrightarrow {AC} } \right|\) thì B nằm giữa A và C.
Trường hợp \(\overrightarrow {AB}\) và \(\overrightarrow {AC}\) ngược hướng thì A nằm giữa B và C.
7. Giải bài 1.7 trang 10 SBT Hình học 10
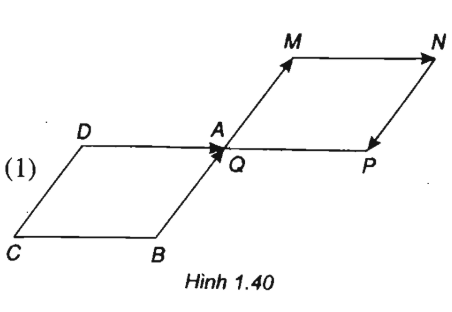
Cho hình bình hành ABCD. Dựng \(\overrightarrow {AM} = \overrightarrow {BA} , \overrightarrow {MN} = \overrightarrow {DA} \), \(\overrightarrow {NP} = \overrightarrow {DC} \), \(\overrightarrow {PQ} = \overrightarrow {BC} \).
Chứng minh \(\overrightarrow {AQ} = \overrightarrow 0\)
Phương pháp giải
Dựng hình và chứng minh như sau:
- Chứng minh tứ giác AMNP là hình bình hành. (1)
- Chứng minh tứ giác MNPQ là hình bình hành (2).
- Từ (1) và (2) suy ra A = Q hay \(\overrightarrow {AQ} = \overrightarrow 0\)
Hướng dẫn giải
\(\overrightarrow {AM} = \overrightarrow {BA}\)
\(\overrightarrow {NP} = \overrightarrow {DC} = \overrightarrow {AB}\)
Suy ra AM = NP và AM // NP. Vậy tứ giác AMNP là hình bình hành. (1)
Ta có \(\overrightarrow {PQ} = \overrightarrow {BC}\)
\(\overrightarrow {MN} = \overrightarrow {DA} = \overrightarrow {CB}\)
Suy ra PQ = MN và P Q // MN . Vậy tứ giác MNPQ là hình bình hành (2).
Từ (1) và (2) suy ra A = Q hay \(\overrightarrow {AQ} = \overrightarrow 0\)
Các em hãy luyện tập bài trắc nghiệm Các định nghĩa Toán 10 sau để nắm rõ thêm kiến thức bài học.