Giải bài tập SBT Toán 10 Bài 2: Tổng và hiệu của hai vec tơ
eLib xin chia sẻ với các em học sinh lớp 10 nội dung giải bài tập SBT bài Tổng và hiệu của hai vec tơ bên dưới đây. Với nội dung đầy đủ 12 bài tập trang 21 đi kèm đó là phương pháp và hướng dẫn giải chi tiết, hi vọng rằng đây sẽ là tài liệu giúp các em học tập tốt hơn. Sau đây mời các em cùng tham khảo.
Mục lục nội dung
1. Giải bài 1.8 trang 21 SBT Hình học 10
2. Giải bài 1.9 trang 21 SBT Hình học 10
3. Giải bài 1.10 trang 21 SBT Hình học 10
4. Giải bài 1.11 trang 21 SBT Hình học 10
5. Giải bài 1.12 trang 21 SBT Hình học 10
6. Giải bài 1.13 trang 21 SBT Hình học 10
7. Giải bài 1.14 trang 21 SBT Hình học 10
8. Giải bài 1.15 trang 21 SBT Hình học 10
9. Giải bài 1.16 trang 21 SBT Hình học 10
10. Giải bài 1.17 trang 21 SBT Hình học 10

1. Giải bài 1.8 trang 21 SBT Hình học 10
Cho năm điểm A, B, C, D và E. Hãy xác định tổng \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DE}\)
Phương pháp giải
Sử dụng quy tắc ba điểm \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Hướng dẫn giải
\(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DE} \)\( = \overrightarrow {AC} + \overrightarrow {CD} + \overrightarrow {DE} \) \( = \overrightarrow {AD} + \overrightarrow {DE} = \overrightarrow {AE}\)
2. Giải bài 1.9 trang 21 SBT Hình học 10
Cho bốn điểm A, B, C và D. Chứng minh \(\overrightarrow {AB} - \overrightarrow {CD} = \overrightarrow {AC} - \overrightarrow {BD}\)
Phương pháp giải
Chuyển vế và sử dụng quy tắc ba điểm \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Hướng dẫn giải
\(\overrightarrow {AB} - \overrightarrow {CD} = \overrightarrow {AC} - \overrightarrow {BD} \)\( \Leftrightarrow \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AC} + \overrightarrow {CD} \) \( \Leftrightarrow \overrightarrow {AD} = \overrightarrow {AD}\,\, (luôn \,\,đúng)\)
Vậy ta có điều phải chứng minh.
3. Giải bài 1.10 trang 21 SBT Hình học 10
Cho hai vec tơ \(\overrightarrow a\) và \(\overrightarrow b\) sao cho \(\overrightarrow a + \overrightarrow b = \overrightarrow 0\)
a) Dựng \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b\). Chứng minh O là trung điểm của AB.
b) Dựng \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b\). Chứng minh \(O \equiv B\)
Phương pháp giải
Sử dụng quy tắc ba điểm \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC}\)
Hướng dẫn giải
a) \(\overrightarrow a + \overrightarrow b = \overrightarrow 0 \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow 0 \)\( \Leftrightarrow \overrightarrow {OB} = - \overrightarrow {OA} \Rightarrow OB = OA\)
Do đó ba điểm A, O, B thẳng hàng và điểm O ở giữa A và B.
Suy ra O là trung điểm của AB.
b)
\(\overrightarrow a + \overrightarrow b = \overrightarrow 0 \Leftrightarrow \overrightarrow {OA} + \overrightarrow {AB} = \overrightarrow 0 \)\( \Leftrightarrow \overrightarrow {OB} = \overrightarrow 0 \Rightarrow B \equiv O\)
4. Giải bài 1.11 trang 21 SBT Hình học 10
Gọi O là tâm của tam giác đều ABC. Chứng minh rằng \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0\)
Phương pháp giải
Sử dụng tính chất trọng tâm: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0\)
Hướng dẫn giải
Trong tam giác đều ABC, tâm O của đường tròn ngoại tiếp cũng là trọng tâm của tam giác.
Vậy \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0\)
5. Giải bài 1.12 trang 21 SBT Hình học 10
Gọi O là giao điểm hai đường chéo của hình bình hành ABCD. Chứng minh rằng
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0\)
Phương pháp giải
Sử dụng tính chất trung điểm \(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0\)
Hướng dẫn giải
ABCD là hình bình hành nên:
+) O là trung điểm AC \(\Rightarrow \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0\)
+) O là trung điểm BD \(\Rightarrow \overrightarrow {OB} + \overrightarrow {OD} = \overrightarrow 0\)
Khi đó,
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \)\( = \left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {OB} + \overrightarrow {OD} } \right)\) \( = \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0\)
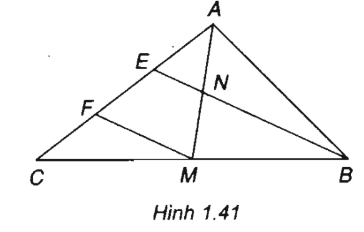
6. Giải bài 1.13 trang 21 SBT Hình học 10
Cho tam giác ABC có trung tuyến AM. Trên cạnh AC lấy hai điểm E và F sao cho AE = EF= FC; BE cắt AM tại N. Chứng minh \(\overrightarrow {NA}\) và \(\overrightarrow {NM}\) là hai vec tơ đối nhau.
Phương pháp giải
Chứng minh EN là đường trung bình của tam giác AFM
Từ đó suy ra N là trung điểm của AM
Vậy ta chứng minh được \(\overrightarrow {NA}\) và \(\overrightarrow {NM}\) là hai vec tơ đối nhau.
Hướng dẫn giải
FM // BE vì FM là đường trung bình của tam giác CEB.
Ta có EA = EF. Vậy EN là đường trung bình của tam giác AFM
Do đó N là trung điểm của AM và \(\overrightarrow {NA} = - \overrightarrow {NM}\)
7. Giải bài 1.14 trang 21 SBT Hình học 10
Cho hai điểm phân biệt A và B. Tìm điểm M thỏa mãn một trong các điều kiện sau:
a) \(\overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {BA}\)
b) \(\overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {AB}\)
c) \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0\)
Phương pháp giải
- Sử dụng công thức tính hiệu hai véc tơ \(\overrightarrow{a}- \overrightarrow{b} = \overrightarrow{a} + (-\overrightarrow{b})\)
- Sử dụng tính chất trung điểm \(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0\)
Hướng dẫn giải
a) \(\overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {BA} \Leftrightarrow \overrightarrow {BA} = \overrightarrow {BA}\)
Vậy mọi điểm M đều thỏa mãn bài toán.
b) \(\overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {AB} \Leftrightarrow \overrightarrow {BA} = \overrightarrow {AB} \Leftrightarrow A \equiv B,\) vô lí.
Vậy không có điểm M nào thỏa mãn bài toán.
c) \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MA} = - \overrightarrow {MB} \)
Vậy M là trung điểm của đoạn thẳng AB.
8. Giải bài 1.15 trang 21 SBT Hình học 10
Cho tam giác ABC. Chứng minh rằng nếu \(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right| = \left| {\overrightarrow {CA} - \overrightarrow {CB} } \right|\) thì tam giác ABC là tam giác vuông tại C.
Phương pháp giải
- Dựng hình bình hành CADB.
- Sử dụng quy tắc hình bình hành quy tắc trừ véc tơ để nhận xét độ dài các véc tơ.
Nếu ABCD là hình bình hành thì \(\overrightarrow{AB} + \overrightarrow{AD} = \overrightarrow{AC}\)
Công thức tính hiệu hai véc tơ \(\overrightarrow{a}- \overrightarrow{b} = \overrightarrow{a} + (-\overrightarrow{b})\)
Hướng dẫn giải
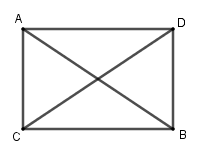
Vẽ hình bình hành CADB. Ta có \(\overrightarrow {CA} + \overrightarrow {CB} = \overrightarrow {CD}\), do đó \(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right| = CD\)
Vì \(\overrightarrow {CA} - \overrightarrow {CB} = \overrightarrow {BA}, \,\,Do \,\,đó \,\, \left| {\overrightarrow {CA} - \overrightarrow {CB} } \right| = BA\)
Từ \(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right| = \left| {\overrightarrow {CA} - \overrightarrow {CB} } \right|\) suy ra CD = AB
Vậy tứ giác CADB là hình chữ nhật. Ta có tam giác ABC vuông tại C.
9. Giải bài 1.16 trang 21 SBT Hình học 10
Cho ngũ giác ABCDE. Chứng minh \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {AE} - \overrightarrow {DE}\)
Phương pháp giải
Sử dụng quy tắc ba điểm \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC}\) và \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB}\)
Hướng dẫn giải
\(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {AE} - \overrightarrow {DE} \)\( \Leftrightarrow \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AE} + \overrightarrow {ED} \) \( \Leftrightarrow \overrightarrow {AD} = \overrightarrow {AD}\)
10. Giải bài 1.17 trang 21 SBT Hình học 10
Cho ba điểm O, A, B không thẳng hàng. Với điều kiện nào thì vec tơ \(\overrightarrow {OA} + \overrightarrow {OB}\) nằm trên đường phân giác của góc \(\widehat {AOB}\)?
Phương pháp giải
Sử dụng quy tắc hình bình hành
Nếu ABCD là hình bình hành thì \(\overrightarrow{AB} + \overrightarrow{AD} = \overrightarrow{AC}\)
Hướng dẫn giải
\(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC}\) trong đó OACB là hình bình hành.
OC là phân giác góc \(\widehat {AOB}\) khi và chỉ khi OACB là hình thoi, tức là OA = OB
11. Giải bài 1.18 trang 21 SBT Hình học 10
Cho hai lực \(\overrightarrow {{F_1}}\) và \(\overrightarrow {{F_2}}\) có điểm đặt O và tạo với nhau góc \({60^0}\). Tìm cường độ tổng hợp lực của hai lực ấy biết rằng cường độ của hai lực \(\overrightarrow {{F_1}}\) và \(\overrightarrow {{F_2}}\) đều là 100N.
Phương pháp giải
Sử dụng quy tắc hình bình hành
Nếu ABCD là hình bình hành thì \(\overrightarrow{AB} + \overrightarrow{AD} = \overrightarrow{AC}\)
Hướng dẫn giải
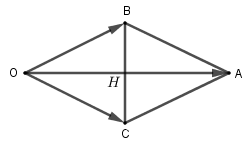
Cố định điểm O, dựng véc tơ \(\overrightarrow {OB} = \overrightarrow {{F_1}} ,\overrightarrow {OC} = \overrightarrow {{F_2}}\)
Dựng hình bình hành OBAC ta có:
\(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OA} \) \( \Rightarrow \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = OA\)
Xét hình bình hành OBAC có OB = OC = 100 nên là hình thoi.
\(\Rightarrow OA \bot BC\) tại H.
Mà \(\widehat {BOC} = {60^0}\) nên tam giác BOC đều.
Do đó BC=100 và \(BH = \frac{1}{2}BC = 50\)
Theo pitago \(OH = \sqrt {O{B^2} - B{H^2}} = \sqrt {{{100}^2} - {{50}^2}} = 50\sqrt 3\)
Vậy cường độ của hợp lực là \(OA = 2OH = 100\sqrt 3 N\)
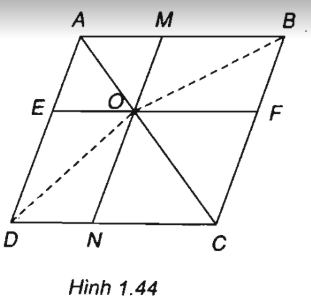
12. Giải bài 1.19 trang 21 SBT Hình học 10
Cho hình bình hành ABCD. Gọi O là một điểm bất kì trên đường chéo AC. Qua O kẻ các đường thẳng song song với các cạnh của hình bình hành. Các đường thẳng này cắt AB và DC lần lượt tại M và N, cắt AD và BC lần lượt tại E và F. Chứng minh rằng:
a) \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {OD}\)
b) \(\overrightarrow {BD} = \overrightarrow {ME} + \overrightarrow {FN}\)
Phương pháp giải
a) Chuyển vế và thực hiện phép trừ các véc tơ.
b) Sử dụng quy tắc hình bình hành
Nếu ABCD là hình bình hành thì \(\overrightarrow{AB} + \overrightarrow{AD} = \overrightarrow{AC}\)
Hướng dẫn giải
a)
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} ; \overrightarrow {DC} = \overrightarrow {OC} - \overrightarrow {OD}\)
Vì \(\overrightarrow {AB} = \overrightarrow {DC}\) nên ta có \(\overrightarrow {OB} - \overrightarrow {OA} = \overrightarrow {OC} - \overrightarrow {OD}\)
Vậy \(\overrightarrow {OB} + \overrightarrow {OD} = \overrightarrow {OA} + \overrightarrow {OC}\)
b) Tứ giác AMOE là hình bình hành nên ta có \(\overrightarrow {ME} = \overrightarrow {MA} + \overrightarrow {MO}\) (1)
Tứ giác OFCN là hình bình hành nên ta có \(\overrightarrow {FN} = \overrightarrow {FO} + \overrightarrow {FC}\) (2)
Từ (1) và (2) suy ra \(\overrightarrow {ME} + \overrightarrow {FN} \)
\(= \overrightarrow {MA} + \overrightarrow {MO} + \overrightarrow {FO} + \overrightarrow {FC}\)
\(=(\overrightarrow {MA} + \overrightarrow {FO} ) + (\overrightarrow {MO} + \overrightarrow {FC})\)
\(\begin{array}{l} = \left( {\overrightarrow {MA} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {BF} + \overrightarrow {FC} } \right)\\ = \left( {\overrightarrow {BM} + \overrightarrow {MA} } \right) + \left( {\overrightarrow {BF} + \overrightarrow {FC} } \right) \end{array}\)
(Vì \(\overrightarrow {FO} = \overrightarrow {BM} ,\overrightarrow {MO} = \overrightarrow {BF}\))
\(= \overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BD}\)
Vậy \(\overrightarrow {BD} = \overrightarrow {ME} + \overrightarrow {FN}\)
Các em hãy luyện tập bài trắc nghiệm Tổng và hiệu của hai vec tơ Toán 10 sau để nắm rõ thêm kiến thức bài học.