Giải bài tập SBT Toán 10 Bài 3: Hàm số bậc hai
Mời quý thầy cô giáo và các em học sinh cùng tham khảo nội dung giải bài tập SBT trang 41, 42 Toán 10 dưới đây. Tài liệu gồm 9 bài tập có hướng dẫn giải và đáp án chi tiết sẽ giúp các em vừa ôn tập kiến thức vừa nâng cao kĩ năng giải bài tập đồng thời có kế hoạch học tập cụ thể. Chúc các em học tập thật tốt!
Mục lục nội dung
1. Giải bài 2.18 trang 41 SBT Đại số 10
2. Giải bài 2.19 trang 41 SBT Đại số 10
3. Giải bài 2.20 trang 41 SBT Đại số 10
4. Giải bài 2.21 trang 42 SBT Đại số 10
5. Giải bài 2.22 trang 42 SBT Đại số 10
6. Giải bài 2.23 trang 42 SBT Đại số 10
7. Giải bài 2.24 trang 42 SBT Đại số 10

1. Giải bài 2.18 trang 41 SBT Đại số 10
Xác định trục đối xứng, tọa độ đỉnh, giao điểm với trục tung và trục hoành của parabol.
a) \(y = 2{x^2} - x - 2\)
b) \(y = - 2{x^2} - x + 2\)
Phương pháp giải
Đồ thị của hàm số bậc hai \(y = a{x^2} + bx + c\) là một parabol có đỉnh là điểm \(I\left( { - \dfrac{b}{{2a}};\dfrac{{ - \Delta }}{{4a}}} \right)\), có trục đối xứng là \(x = - \dfrac{b}{{2a}}\)
Hướng dẫn giải
a) Ta có a = 2; b = - 1; c = - 2.Ta có \(\Delta = {( - 1)^2} - 4.2.( - 2) = 17\)
Trục đối xứng là đường thẳng \(x = \dfrac{1}{4} \,\, đỉnh \,\, I(\dfrac{1}{4}; - \dfrac{{17}}{8})\); giao với trục tung tại điểm (0;-2)
Để tìm giao điểm với trục hoành ta giải phương trình
\(2{x^2} - x - 2 = 0 \Leftrightarrow {x_{1,2}} = \dfrac{{1 \pm \sqrt {17} }}{4}\)
Vậy các giao điểm với trục hoành là \((\dfrac{{1 + \sqrt {17} }}{4};0)\) và \((\dfrac{{1 - \sqrt {17} }}{4};0)\)
b) Ta có a = - 2; b = - 1; c = 2.Ta có \(\Delta = {( - 1)^2} - 4.2.( - 2) = 17\)
Trục đối xứng là đường thẳng \(x = - \dfrac{1}{4} \,\, đỉnh \,\, I( - \dfrac{1}{4}; - \dfrac{{17}}{8})\); giao với trục tung tại điểm (0;-2)
Để tìm giao điểm với trục hoành ta giải phương trình
\(- 2{x^2} - x + 2 = 0 \Leftrightarrow \) \({x_{1,2}} = \dfrac{{ - 1 \pm \sqrt {17} }}{4}\)
Vậy các giao điểm với trục hoành là
\(\left( {\dfrac{{ - 1 + \sqrt {17} }}{4};0} \right) \,\, và \,\, \left( {\dfrac{{ - 1 - \sqrt {17} }}{4};0} \right)\)
2. Giải bài 2.19 trang 41 SBT Đại số 10
Lập bảng biến thiên và vẽ đồ thị của hàm số bậc hai
a) \(y = 2{x^2} + 4x - 6\)
b) \(y = - 3{x^2} - 6x + 4\)
c) \(y = \sqrt 3 {x^2} + 2\sqrt 3 x + 2\)
d) \(y = - 2({x^2} + 1)\)
Phương pháp giải
Nếu a > 0 thì hàm số \(y = a{x^2} + bx + c\)
+) Nghịch biến trên khoảng \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\)
+) Đồng biến trên khoảng \(\left( { - \frac{b}{{2a}}; + \infty } \right)\)
Nếu a < 0 thì hàm số \(y = a{x^2} + bx + c\)
+) Đồng biến trên khoảng \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\)
+) Nghịch biến trên khoảng \(\left( { - \frac{b}{{2a}}; + \infty } \right)\)
Hướng dẫn giải
a) Hàm số bậc hai đã cho có a = 2; b = 4;c = −6
Vậy \( - \frac{b}{{2a}} = - 1;\Delta = {b^2} - 4ac = 64; - \frac{\Delta }{{4a}} = - 8\)
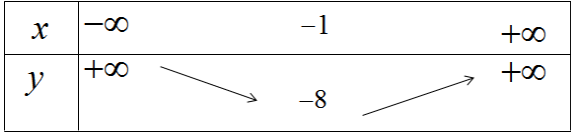
Vì a > 0, ta có bảng biến thiên
Hàm số nghịch biến trên khoảng (−∞;−1), đồng biến trên khoảng (−1;+∞).
Để vẽ đồ thị ta có trục đối xứng là đường thẳng x = −1; đỉnh I(−1;−8); giao với tục tung tại điểm (0;−6); giao với trục hoành tại các điểm (−3;0) và (1;0).
Đồ thị của hàm số y = 2x2+4x−6 được vẽ trên hình
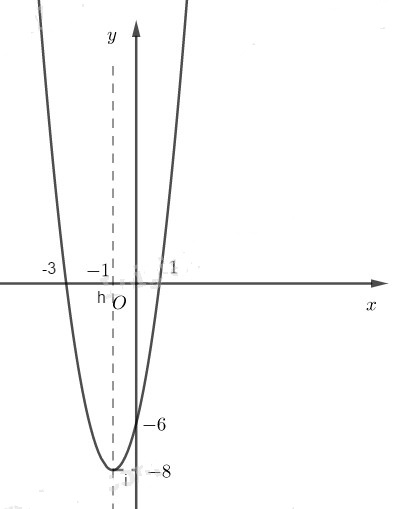
b) Hàm số bậc hai đã cho có a = −3; b = −6; c = 4
Vậy \( - \frac{b}{{2a}} = - 1,\Delta = {b^2} - 4ac = 84, - \frac{\Delta }{{4a}} = 7\)
Vì a < 0, ta có bảng biến thiên
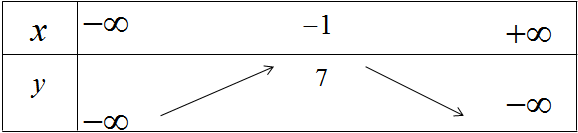
Hàm số đồng biến trên khoảng (−∞;−1) và nghịch biến trên khoảng (−1;+∞).
Để vẽ đồ thị ta có trục đối xứng là đường thẳng x = −1; đỉnh I(−1;7) giao với tục tung tại điểm (0;4)
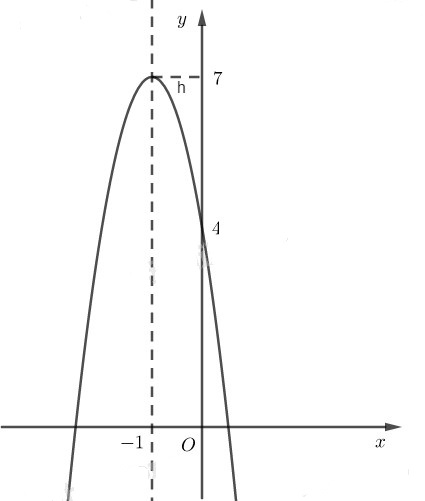
c) Hàm số bậc hai đã cho có \(a = \sqrt 3 ;b = 2\sqrt 3 ,c = 2\)
Vậy \(- \frac{b}{{2a}} = - 1,\Delta = {b^2} - 4ac = 12 - 8\sqrt 3 , - \frac{\Delta }{{4a}} = 2 - \sqrt 3 \)
Vì a > 0, ta có bảng biến thiên
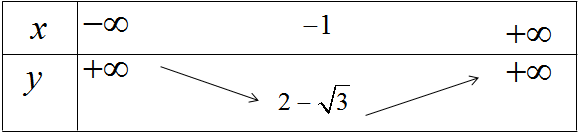
Hàm số nghịch biến trên khoảng (−∞;−1) và đồng biến trên khoảng (−1;+∞).
Để vẽ đồ thị ta có trục đối xứng là đường thẳng x = −1; đỉnh \(I\left( { - 1;2 - \sqrt 3 } \right)\) giao với tục tung tại điểm (0;2)
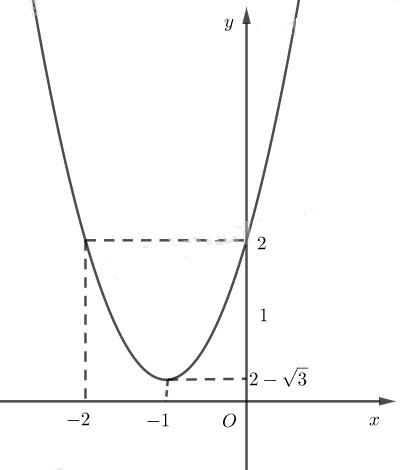
3. Giải bài 2.20 trang 41 SBT Đại số 10
Viết phương trình của parabol \(y = a{x^2} + bx + c\) ứng với mỗi đồ thị dưới đây
Phương pháp giải
Xác định các hệ số a, b, c dựa vào đồ thị của hàm số.
Hướng dẫn giải
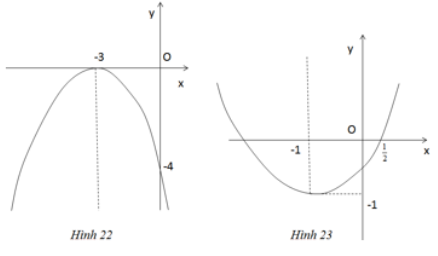
a) Dựa trên đồ thị (h.22) ta thấy parabol có đỉnh I( - 3;0) và đi qua điểm (0; - 4)
Như vậy \(c = - 4; - \dfrac{b}{{2a}} = - 3 \Leftrightarrow b = 6a\)
Thay c = - 4 và b = 6a vào biểu thức
\(\Delta = {b^2} - 4ac = 0 = > 36{a^2} + 16a = 0 = > a = - \dfrac{4}{9}\,\, (vì a \ne 0) \,\, và \,\, b = - \dfrac{8}{3}\)
Vậy phương trình của parabol là \(y = - \dfrac{4}{9}{x^2} - \dfrac{8}{3}x - 4\)
b) Dựa trên đồ thị (h.23) ta thấy parabol có đỉnh I( - 1; - 1) và đi qua điểm \(\left( {\dfrac{1}{2};0} \right)\)
Như vậy \(\left\{ {\begin{array}{*{20}{c}}{\dfrac{1}{4}a + \dfrac{1}{2}b + c = 0}\\{ - \dfrac{b}{{2a}} = - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{b = 2a}\\{c = - \dfrac{5}{4}a}\end{array}} \right.\)
Thay vào biểu thức
\(\Delta = {b^2} - 4ac = - 1 = > 4{a^2} + 5a + 1 = 0 = > a = \dfrac{4}{9}\,\, (vì \,\,a > 0)\Rightarrow b = \dfrac{8}{9};c = \dfrac{{ - 5}}{9}\)
\(y = \dfrac{4}{9}{x^2} + \dfrac{8}{9}x - \dfrac{5}{9}\)
4. Giải bài 2.21 trang 42 SBT Đại số 10
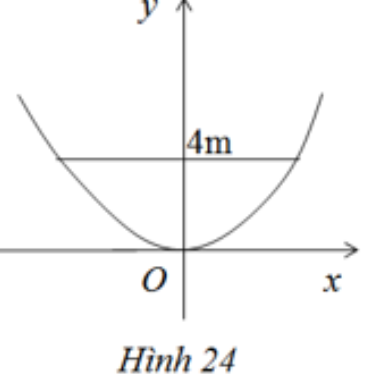
Một chiếc ăng – ten chảo parabol có chiều cao h = 0,5 m và đường kính d = 4 m. Ở mặt cắt qua trục ta được một parabol dạng \(y = a{x^2}\)(h.24). Hãy xác định hệ số a.
Phương pháp giải
Dựa vào hình vẽ tìm điểm mà đồ thị hàm số đi qua.
Hướng dẫn giải
Đồ thị hàm số \(y = a{x^2}\) nhận đường thẳng x = 0 làm trục đối xứng và đồ thị đi qua điểm \(\left( {2;\dfrac{1}{2}} \right)\)
Suy ra \(4a = \dfrac{1}{2} \Rightarrow a = \dfrac{1}{8}\)
Hệ số \(a = \dfrac{1}{8}\)
5. Giải bài 2.22 trang 42 SBT Đại số 10
Một chiếc cổng hình parabol dạng \(y = - \dfrac{1}{2}{x^2}\) có chiều rộng d = 8m. Hãy tính chiều cao h của cổng (hình dưới).

Phương pháp giải
Dựa vào hình vẽ tìm điểm mà đồ thị hàm số đi qua.
Hướng dẫn giải
Đồ thị hàm số \(y = - \dfrac{1}{2}{x^2}\) nhận đường thẳng x = 0 làm trục đối xứng và đồ thị đi qua điểm \(\left( {4; - h} \right)\)
Suy ra \(- h = - \dfrac{1}{2}{.4^2} \Rightarrow h = 8\)
Chiều cao của cổng h = 8m
6. Giải bài 2.23 trang 42 SBT Đại số 10
Tọa độ đỉnh của paranol \(y = - \dfrac{1}{2}{x^2} + 6x + 1\) là
A. \(I\left( {6;19} \right)\)
B. \(I\left( {6;17} \right)\)
C. \(I\left( { - 6; - 43} \right)\)
D. \(I\left( { - 6;41} \right)\)
Phương pháp giải
Đồ thị của hàm số bậc hai \(y = a{x^2} + bx + c\) là một parabol có đỉnh là điểm \(I\left( { - \dfrac{b}{{2a}};\dfrac{{ - \Delta }}{{4a}}} \right)\)
Hướng dẫn giải
Ta có: \(a = - \dfrac{1}{2};b = 6;c = 1. \,\, Suy \,\, ra \,\, - \dfrac{b}{{2a}} = 6;\Delta = {b^2} - 4ac = 38; - \dfrac{\Delta }{{4a}} = 19\)
Vậy đỉnh của parabol là \(I\left( {6;19} \right)\)
Đáp án đúng A
7. Giải bài 2.24 trang 42 SBT Đại số 10
Trục đối xứng của parabol \(y = \dfrac{1}{5}{x^2} + 2x + 7\) là
A. y = - 3
B. y = - 5
C. x = - 5
D. x = 5
Phương pháp giải
Đồ thị của hàm số bậc hai \(y = a{x^2} + bx + c\) là một parabol có có trục đối xứng là \(x = - \dfrac{b}{{2a}}\)
Hướng dẫn giải
Ta có: \(a = \dfrac{1}{5};b = 2;c = 7\). Suy ra \(- \dfrac{b}{{2a}} = - 5\)
Vậy trục đối xứng của parabol là x = - 5
Đáp án đúng C
8. Giải bài 2.25 trang 42 SBT Đại số 10
Hàm số bậc hai \(y = a{x^2} + bx - 6\) có đồ thị đi qua hai điểm \(A\left( {1;1} \right)\) và \(B\left( {2;2} \right)\) là
A. \(y = 2{x^2} + 5x - 6\)
B. \(y = - 3{x^2} + 10x - 6\)
C. \(y = - 2{x^2} + 8x - 6\)
D. \(y = 3{x^2} + 3x - 6\)
Phương pháp giải
Thay tọa độ của các điểm thuộc đồ thị vào hàm số để tìm ra các hệ số a, b
Hướng dẫn giải
Do đồ thị đi qua hai điểm \(A\left( {1;1} \right)\) và \(B\left( {2;2} \right)\) nên ta có:
\(\left\{ {\begin{array}{*{20}{c}}{a + b - 6 = 1}\\{4a + 2b - 6 = 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - 3}\\{b = 10}\end{array}} \right.\)
Đáp án đúng B
9. Giải bài 2.26 trang 42 SBT Đại số 10
Hàm số bậc hai \(y = a{x^2} - 2x + c\) có đồ thị với đỉnh \(I\left( {2; - 1} \right)\) là
A. \(y = \dfrac{1}{2}{x^2} - 2x + 1\)
B. \(y = \dfrac{1}{2}{x^2} - 2x + 3\)
C. \(y = {x^2} - 2x - 1\)
D. \(y = 2{x^2} - 2x - 5\)
Phương pháp giải
Đồ thị của hàm số bậc hai \(y = a{x^2} + bx + c\) là một parabol có đỉnh là điểm \(I\left( { - \dfrac{b}{{2a}};\dfrac{{ - \Delta }}{{4a}}} \right)\)
Hướng dẫn giải
Ta có: \(- \dfrac{b}{{2a}} = 2 \Rightarrow - \dfrac{{ - 2}}{{2a}} = 2 \Rightarrow a = \dfrac{1}{2}\)
\(\dfrac{{ - \Delta }}{{4a}} = - 1 \Rightarrow {b^2} - 4ac = 4a = 2 \Rightarrow 4 - 2c = 2 \Rightarrow c = 1\)
Đáp án đúng A
Các em hãy luyện tập bài trắc nghiệm Hàm số bậc hai Toán 10 sau để nắm rõ thêm kiến thức bài học.