Giải bài tập SBT Toán 10 Bài 4: Hệ trục tọa độ
Để giúp các em học sinh lớp 10 học tập thật tốt môn Toán, eLib xin giới thiệu nội dung giải bài tập SBT trang 41, 42 bên dưới đây. Tài liệu gồm tất cả các bài tập có phương pháp và hướng dẫn giải chi tiết, rõ ràng, sẽ giúp các em ôn tập lại kiến thức, cũng cố kĩ năng làm bài hiệu quả. Mời các em cùng tham khảo.
Mục lục nội dung
1. Giải bài 1.36 trang 41 SBT Hình học 10
2. Giải bài 1.37 trang 41 SBT Hình học 10
3. Giải bài 1.38 trang 42 SBT Hình học 10
4. Giải bài 1.39 trang 42 SBT Hình học 10
5. Giải bài 1.40 trang 42 SBT Hình học 10
6. Giải bài 1.41 trang 42 SBT Hình học 10
7. Giải bài 1.42 trang 42 SBT Hình học 10
8. Giải bài 1.43 trang 42 SBT Hình học 10
9. Giải bài 1.44 trang 42 SBT Hình học 10
10. Giải bài 1.45 trang 42 SBT Hình học 10

1. Giải bài 1.36 trang 41 SBT Hình học 10
Viết tọa độ của các vec tơ sau:
\(\overrightarrow a = 2\overrightarrow i + 3\overrightarrow j \)
\(\overrightarrow b = \dfrac{1}{3}\overrightarrow i - 5\overrightarrow j \)
\(\overrightarrow c = 3\overrightarrow i \)
\(\overrightarrow d = - 2\overrightarrow j\)
Phương pháp giải
Sử dụng định nghĩa tọa độ véc tơ:
Nếu \(\overrightarrow a = x\overrightarrow i + y\overrightarrow j\) thì cặp số \(\left( {x;y} \right)\) được gọi là tọa độ của véc tơ \(\overrightarrow a\)
Hướng dẫn giải
+) \(\overrightarrow a = 2\overrightarrow i + 3\overrightarrow j \Rightarrow \overrightarrow a = (2;3)\)
+) \(\overrightarrow b = \dfrac{1}{3}\overrightarrow i - 5\overrightarrow j\Rightarrow \overrightarrow b = \left( {\dfrac{1}{3}; - 5} \right)\)
+) \(\overrightarrow c = 3\overrightarrow i = 3\overrightarrow i + 0\overrightarrow j \Rightarrow \overrightarrow c = (3;0)\)
+) \(\overrightarrow d = - 2\overrightarrow j = 0\overrightarrow i - 2\overrightarrow j \Rightarrow \overrightarrow d = (0; - 2)\)
2. Giải bài 1.37 trang 41 SBT Hình học 10
Viết vec tơ \(\overrightarrow u\) dưới dạng \(\overrightarrow u = x\overrightarrow i + y\overrightarrow j \) khi biết tọa độ của \(\overrightarrow u\) là: (2; - 3), ( - 1;4), (2;0), (0; - 1), (0;0)
Phương pháp giải
Sử dụng định nghĩa tọa độ véc tơ:
Nếu \(\overrightarrow a = x\overrightarrow i + y\overrightarrow j\) thì cặp số \(\left( {x;y} \right)\) được gọi là tọa độ của véc tơ \(\overrightarrow a\)
Hướng dẫn giải
\(\overrightarrow u = (2; - 3) \Rightarrow \overrightarrow u = 2\overrightarrow i - 3\overrightarrow j \)
\(\overrightarrow u = ( - 1;4) \Rightarrow \overrightarrow u = - \overrightarrow i + 4\overrightarrow j \)
\(\overrightarrow u = (2;0) \Rightarrow \overrightarrow u = 2\overrightarrow i \)
\(\overrightarrow u = (0; - 1) \Rightarrow \overrightarrow u = - \overrightarrow j \)
\(\overrightarrow u = (0;0) \Rightarrow \overrightarrow u = 0\overrightarrow i + 0\overrightarrow j = \overrightarrow 0 \)
3. Giải bài 1.38 trang 42 SBT Hình học 10
Cho \(\overrightarrow a = (1; - 2),\overrightarrow b (0;3)\). Tìm tọa độ của các vec tơ \(\overrightarrow x = \overrightarrow a + \overrightarrow b ,\overrightarrow y = \overrightarrow a - \overrightarrow b ,\overrightarrow z = 3\overrightarrow a - 4\overrightarrow b\)
Phương pháp giải
Sử dụng công thức \(k\overrightarrow a \pm l\overrightarrow b = \left( {kx \pm lx';ky \pm ly'} \right)\)
Hướng dẫn giải
\(\overrightarrow x = \overrightarrow a + \overrightarrow b = \left( {1 + 0; - 2 + 3} \right) = \left( {1;1} \right)\)
\(\overrightarrow y = \overrightarrow a - \overrightarrow b = \left( {1 - 0; - 2 - 3} \right) = \left( {1; - 5} \right)\)
\(\overrightarrow z = 3\overrightarrow a - 4\overrightarrow b \)\( = \left( {3.1 - 4.0;3.\left( { - 2} \right) - 4.3} \right)\)\( = \left( {3; - 18} \right)\)
4. Giải bài 1.39 trang 42 SBT Hình học 10
Xét xem các cặp vec tơ sau có cùng phương không? Trong trường hợp cùng phương thì xét xem chúng cùng hướng hay ngược hướng.
a) \(\overrightarrow a = (2;3),\overrightarrow b = ( - 10; - 15)\)
b) \(\overrightarrow u = (0;7),\overrightarrow v = (0;8)\)
c) \(\overrightarrow m = ( - 2;1),\overrightarrow b = ( - 6;3)\)
d) \(\overrightarrow c = (3;4),\overrightarrow d = (6;9)\)
e) \(\overrightarrow e = (0;5),\overrightarrow f = (3;0)\)
Phương pháp giải
Sử sụng lý thuyết : Nếu \(\overrightarrow a = k\overrightarrow b\) mà k > 0 thì hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b\) cùng hướng.
Nếu \(\overrightarrow a = k\overrightarrow b\) mà k < 0 thì hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng.
Hướng dẫn giải
a) \(\overrightarrow a ,\overrightarrow b \) ngược hướng vì \(\overrightarrow b = - 5\overrightarrow a\)
b) \(\overrightarrow u ,\overrightarrow v\) cùng hướng vì \(\overrightarrow u = \dfrac{7}{8}\overrightarrow v\)
c) \(\overrightarrow m ,\overrightarrow n \)cùng hướng vì \(\overrightarrow n = 3\overrightarrow m\)
d) \(\overrightarrow c ,\overrightarrow d\) không cùng phương vì không tồn tại số k nào để \(\overrightarrow c = k\overrightarrow d\)
e) \(\overrightarrow e ,\overrightarrow f\) không cùng phương vì không tồn tại số k nào để \(\overrightarrow e = k\overrightarrow f \)
5. Giải bài 1.40 trang 42 SBT Hình học 10
a) Cho A( - 1;8), B(1;6), C(3;4). Chứng minh ba điểm A, B, C thẳng hàng.
b) Cho A(1;1), B(3;2), C(m + 4;2m + 1). Tìm m để ba điểm A, B, C thẳng hàng.
Phương pháp giải
Ba điểm \(A,B,C\) phân biệt thẳng hàng nếu tồn tại số thực \(k \ne 0\) sao cho \(\overrightarrow {AB} = k\overrightarrow {AC} \)
Hướng dẫn giải
a) \(\overrightarrow {AB} = (2; - 2),\overrightarrow {AC} = (4; - 4)\)
Vậy \(\overrightarrow {AC} = 2\overrightarrow {AB} \Rightarrow \) ba điểm A, B, C thẳng hàng.
b) \(\overrightarrow {AB} = (2;1),\overrightarrow {AC} = (m + 3;2m)\)
Ba điểm A, B, C thẳng hàng
\(\begin{array}{l} \Leftrightarrow \overrightarrow {AC} = k\overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l} m + 3 = k.2\\ 2m = k.1 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} m + 3 = 2k\\ 2m = k \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} m + 3 = 2.2m\\ 2m = k \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} 3m = 3\\ 2m = k \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} m = 1\\ k = 2 \end{array} \right. \end{array}\)
Vậy m = 1.
6. Giải bài 1.41 trang 42 SBT Hình học 10
Cho bốn điểm A( - 2; - 3), B(3;7), C(0;3), D( - 4; - 5). Chứng minh rằng hai đường thẳng AB và CD song song với nhau.
Phương pháp giải
Hai đường thẳng AB và CD song song nếu \(\overrightarrow {AB}\) và \(\overrightarrow {CD}\) cùng phương nhưng \(\overrightarrow {AC}\) và \(\overrightarrow {AB}\) không cùng phương.
Hướng dẫn giải
\(\overrightarrow {AB} = (5;10),\overrightarrow {CD} = ( - 4; - 8). \,\,Ta\,\, có \,\, \overrightarrow {CD} = - \dfrac{4}{5}\overrightarrow {AB}\), vậy hai đường thẳng AB và CD song song hoặc trùng nhau.
Ta có \(\overrightarrow {AC} = \left( {2;6} \right)\) và \(\overrightarrow {AB} = \left( {5;10} \right)\) không trùng phương vì \(\dfrac{5}{2} \ne \dfrac{{10}}{6}\)
Vậy AB // CD
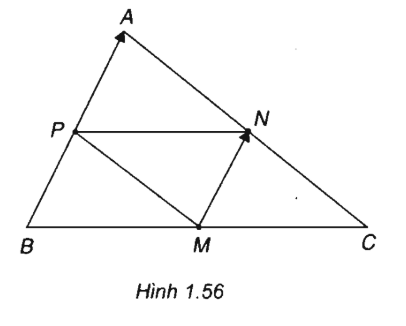
7. Giải bài 1.42 trang 42 SBT Hình học 10
Cho tam giác ABC. Các điểm M(1;1), N(2;3), P(0; - 4) lần lượt là trung điểm các cạnh BC, CA, AB. Tính tọa độ các đỉnh của tam giác.
Phương pháp giải
- Dựng hình
- Ta có: \(\overrightarrow {MN} = (1;2); \overrightarrow {PA} = \left( {{x_A};{y_A} + 4} \right)\)
\(\overrightarrow {PA} = \overrightarrow {MN} \,\, suy\,\, ra \,\,\left\{ \begin{array}{l}{x_A} = 1\\{y_A} + 4 = 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_A} = 1\\{y_A} = - 2\end{array} \right. \)
Tương tự tính được tọa độ diểm B, C
Hướng dẫn giải
Ta có: \(\overrightarrow {MN} = (1;2); \overrightarrow {PA} = \left( {{x_A};{y_A} + 4} \right)\)
Vì \(\overrightarrow {PA} = \overrightarrow {MN} \,\, suy\,\, ra \,\,\left\{ \begin{array}{l}{x_A} = 1\\{y_A} + 4 = 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_A} = 1\\{y_A} = - 2\end{array} \right.\)
Tương tự, ta tính được \(\left\{ \begin{array}{l}{x_B} = - 1\\{y_B} = - 6\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_C} = 3\\{y_C} = 8\end{array} \right.\)
Vậy tọa độ các đỉnh của tam giác là A(1; - 2), B( - 1; - 6), C(3;8)
8. Giải bài 1.43 trang 42 SBT Hình học 10
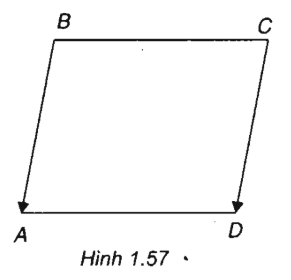
Cho hình bình hành ABCD. Biết A(2; - 3), B(4;5), C(0; - 1). Tính tọa độ của đỉnh D
Phương pháp giải
Dựng hình
Ta có: \(\overrightarrow {BA} = ( - 2; - 8)\)
\(\overrightarrow {CD} = ({x_D};{y_D} + 1)\,\, và \,\, \overrightarrow {BA} = \overrightarrow {CD}\)
Suy ra được tọa độ điểm D cần tìm
Hướng dẫn giải
Ta có: \(\overrightarrow {BA} = ( - 2; - 8)\)
\(\overrightarrow {CD} = ({x_D};{y_D} + 1)\,\,. Vì \,\, \overrightarrow {BA} = \overrightarrow {CD} \,\, nên \,\, \left\{ \begin{array}{l}{x_D} = - 2\\{y_D} + 1 = - 8\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_D} = - 2\\{y_D} = - 9\end{array} \right.\)
Vậy tọa độ đỉnh D( - 2; - 9)
Nhận xét: Ta có thể tính tọa độ đỉnh D dựa vào biểu thức \(\overrightarrow {BD} = \overrightarrow {BA} + \overrightarrow {BC}\)
9. Giải bài 1.44 trang 42 SBT Hình học 10
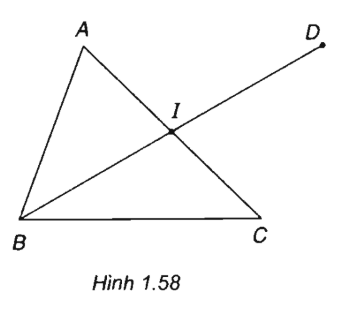
Cho tam giác ABC có A( - 5;6), B( - 4; - 1), C(4;3). Tìm tọa độ trung điểm I của AC. Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
Phương pháp giải
- Sử dụng công thức trung điểm \(\left\{ \begin{array}{l}{x_I} = \dfrac{{{x_A} + {x_C}}}{2}\\{y_I} = \dfrac{{{y_A} + {y_C}}}{2}\end{array} \right.\)
- Tứ giác ABCD là hình bình hành \( \Leftrightarrow I\) là trung điểm của BD
Hướng dẫn giải
Gọi I là trung điểm của AC. Khi đó
\({x_I} = \dfrac{{ - 5 + 4}}{2} = - \dfrac{1}{2},{y_I} = \dfrac{{6 + 3}}{2} = \dfrac{9}{2}\)
Tứ giác ABCD là hình bình hành \(\Leftrightarrow I\) là trung điểm của BD
Vậy
\(\left\{ \begin{array}{l}\dfrac{{{x_D} - 4}}{2} = - \dfrac{1}{2}\\\dfrac{{{y_D} - 1}}{2} = \dfrac{9}{2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_D} - 4 = - 1\\{y_D} - 1 = 9\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 3\\{y_D} = 10\end{array} \right.\)
Vậy tọa độ đỉnh D là (3;10).
10. Giải bài 1.45 trang 42 SBT Hình học 10
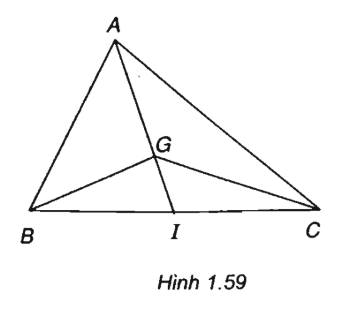
Cho tam giác ABC có A( - 3;6), B(9; - 10), C( - 5;4)
a) Tìm tọa độ của trọng tâm G của tam giác ABC
b) Tìm tọa độ điểm D sao cho tứ giác BGCD là hình bình hành.
Phương pháp giải
a) Sử dụng công thức tọa độ trọng tâm \(\left\{ \begin{array}{l}{x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right.\)
b) Sử dụng tính chất hình bình hành \(\overrightarrow {BG} = \overrightarrow {DC}\)
Hướng dẫn giải
a) Ta có: \(\left\{ \begin{array}{l}{x_G} = \dfrac{{ - 3 + 9 - 5}}{3} = \dfrac{1}{3}\\{y_G} = \dfrac{{6 - 10 + 4}}{3} = 0\end{array} \right.\)
b) Tứ giác BGCD là hình bình hành thì \(\overrightarrow {BG} = \overrightarrow {DC} \)
\(\Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{3} - 9 = - 5 - {x_D}\\0 - \left( { - 10} \right) = 4 - {y_D}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_D} = \dfrac{{11}}{3}\\{y_D} = - 6\end{array} \right.\)
Vậy tọa độ điểm D là \(D\left( {\dfrac{{11}}{3}; - 6} \right)\)
11. Giải bài 1.46 trang 42 SBT Hình học 10
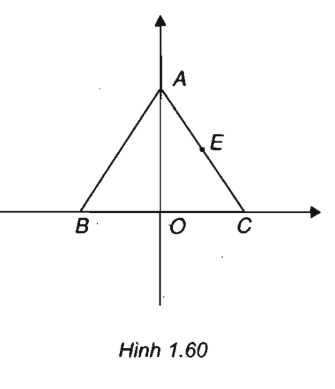
Cho tam giác đều ABC cạnh a. Chọn hệ tọa độ \((O;\overrightarrow i ,\overrightarrow j )\) trong đó O là trung điểm của cạnh BC, \(\overrightarrow i \) cùng hướng với \(\overrightarrow {OC} , \overrightarrow j \) cùng hướng với \(\overrightarrow {OA} \)
a) Tính tọa độ của các đỉnh của tam giác ABC
b) Tìm tọa độ trung điểm E của AC
c) Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC
Phương pháp giải
Dựng hình
a) Do O là trung điểm CB nên \(OB = OC = \dfrac{a}{2}\) và \(OA = \sqrt {A{C^2} - O{C^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2}\)
Từ đó xác định được tọa độ các điểm A, B, C
b) Do E là trung điểm của AC nên \(\left\{ \begin{array}{l}{x_E} = \dfrac{{0 + \dfrac{a}{2}}}{2} = \dfrac{a}{4}\\{y_E} = \dfrac{{\dfrac{{a\sqrt 3 }}{2} + 0}}{2} = \dfrac{{a\sqrt 3 }}{4}\end{array} \right.\)
Suy ra được tọa độ điểm E
c) G là trọng tâm tam giác thì \(\left\{ \begin{array}{l}{x_G} = \dfrac{{0 + \left( { - \dfrac{a}{2}} \right) + \dfrac{a}{2}}}{3} = 0\\{y_G} = \dfrac{{\dfrac{{a\sqrt 3 }}{2} + 0 + 0}}{3} = \dfrac{{a\sqrt 3 }}{6}\end{array} \right.\)
Suy ra được tọa độ điểm G
Hướng dẫn giải
a) Do O là trung điểm CB nên \(OB = OC = \dfrac{a}{2}\) và \(OA = \sqrt {A{C^2} - O{C^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2}\)
Từ hình vẽ ta suy ra \(A\left( {0;\dfrac{{a\sqrt 3 }}{2}} \right),B\left( { - \dfrac{a}{2};0} \right),C\left( {\dfrac{a}{2};0} \right)\)
b) Do E là trung điểm của AC nên \(\left\{ \begin{array}{l}{x_E} = \dfrac{{0 + \dfrac{a}{2}}}{2} = \dfrac{a}{4}\\{y_E} = \dfrac{{\dfrac{{a\sqrt 3 }}{2} + 0}}{2} = \dfrac{{a\sqrt 3 }}{4}\end{array} \right. \,\, nên \,\,E\left( {\dfrac{a}{4};\dfrac{{a\sqrt 3 }}{4}} \right)\)
c) Tâm đường tròn ngoại tiếp tam giác đều trùng với trọng tâm của tam giác.
Gọi G là trọng tâm tam giác thì \(\left\{ \begin{array}{l}{x_G} = \dfrac{{0 + \left( { - \dfrac{a}{2}} \right) + \dfrac{a}{2}}}{3} = 0\\{y_G} = \dfrac{{\dfrac{{a\sqrt 3 }}{2} + 0 + 0}}{3} = \dfrac{{a\sqrt 3 }}{6}\end{array} \right.\,\,hay \,\, G\left( {0;\dfrac{{a\sqrt 3 }}{6}} \right)\)
12. Giải bài 1.47 trang 42 SBT Hình học 10
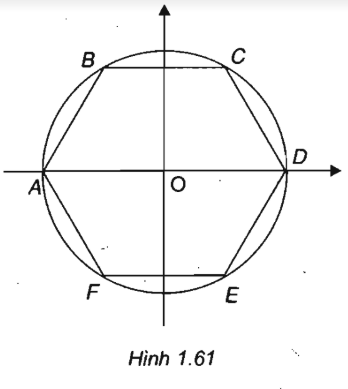
Cho lục giác đều ABCDEF. Chọn hệ tọa độ \((O;\overrightarrow i ,\overrightarrow j )\), trong đó O là tâm của lục giác đều, hai véc tơ \(\overrightarrow i\) và \(\overrightarrow {OD}\) cùng hướng, \(\overrightarrow j\)và \(\overrightarrow {EC}\) cùng hướng . Tính tọa độ các đỉnh của lục giác biết độ dài của lục giác là 6.
Phương pháp giải
Dựng hình, tính độ dài các đoạn thẳng và suy ra tọa độ cần tính.
Hướng dẫn giải
Từ hình vẽ ta thấy \(A\left( { - 6;0} \right)\) và \(D\left( {6;0} \right)\) (do các tam giác AOB và COD đều nên OA = OD = AB = 6)
Gọi H, K lần lượt là hình chiếu của C, B lên trục Ox
Khi đó \(CH = DC\sin {60^0} = \dfrac{{6\sqrt 3 }}{2} = 3\sqrt 3\)
\(OH = \sqrt {O{C^2} - C{H^2}} = \sqrt {{6^2} - {{\left( {3\sqrt 3 } \right)}^2}} = 3\)
Do đó \(C\left( {3;3\sqrt 3 } \right)\)
B đối xứng với C qua Oy nên B(-3; \(3\sqrt 3 \))
E đối xứng với C qua Ox nên E(3; -\(3\sqrt 3 \))
F đối xứng với C qua O nên F(-3; -\(3\sqrt 3 \))
Vậy \(A\left( { - 6;0} \right), D\left( {6;0} \right), B\left( { - 3;3\sqrt 3 } \right), C\left( {3;3\sqrt 3 } \right), E\left( {3; - 3\sqrt 3 } \right), F\left( { - 3; - 3\sqrt 3 } \right)\)
Các em hãy luyện tập bài trắc nghiệm Hệ trục tọa độ Toán 10 sau để nắm rõ thêm kiến thức bài học.