Giải bài tập SGK Vật lý 11 Bài 11: Phương pháp giải một số bài toán về toàn mạch

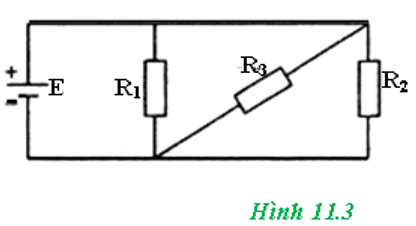
Cho mạch điện có sơ đồ như hình 11.3, trong đó nguồn điện có suất điện động E = 6V và có điện trở trong không đáng kể. Các điện trở R₁ = R₂ = 30Ω, R₃ = 7,5Ω.

a) Tính điện trở tương đương R_N của mạch ngoài.

b) Tính cường độ dòng điện chạy qua mỗi điện trở mạch ngoài.

Phương pháp giải

a) Áp dụng công thức:

\(\frac{1}{{{R_N}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}}\) để tính điện trở tương đương.

b) Áp dụng công thức:

I = U/R để tính cường độ dòng điện.

Hướng dẫn giải

a) Tính điện trở tương đương

- Các điện trở mạch ngoài được mắc song song nhau.

- Ta có: \(\frac{1}{{{R_N}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_2}}}\)

\( \Rightarrow \frac{1}{{{R_N}}} = \frac{1}{{30}} + \frac{1}{{30}} + \frac{1}{{7,5}} \Rightarrow {R_N} = 5\Omega \)

b) Tính cường độ dòng điện

- Nguồn điện có điện trở trong không đáng kể.

- Hiệu điện thế hai đầu nguồn điện:

U = E = 6V

- Cường độ dòng điện qua điện trở 1, 2 và 3 là:  

\(\begin{array}{l} {I_1} = {I_2} = \frac{U}{{{R_1}}} = \frac{U}{{{R_2}}} = \frac{6}{{30}} = 0,2A\\ {I_3} = \frac{U}{{{R_3}}} = \frac{6}{{7,5}} = 0,8A \end{array}\)

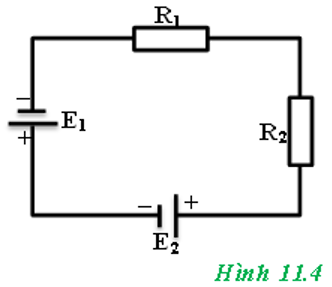
Cho mạch điện có sơ đồ như hình 11.4, trong đó các ắc quy có suất điện động E₁ = 12V; E₂ = 6V và có điện trở không đáng kể. Các điện trở R₁ = 4Ω; R₂ = 8Ω.

a) Tính cường độ dòng điện chạy trong mạch.

b) Tính công suất tiêu thụ điện của mỗi điện trở.

c) Tính công suất của mỗi ắc quy và năng lượng mà mỗi ắc quy cung cấp trong 5 phút.

Phương pháp giải

a) Áp dụng định luật Ohm: I = E_b/R_b để tính cường độ dòng điện.

b) Áp dụng công thức: P = R.I² để tính công suất tiêu thụ điện của mỗi điện trở.

c) Áp dụng các công thức:

+ P = E.I để tính công suất của mỗi ắc quy.

+ A = P.t để tính năng lượng.

Hướng dẫn giải

a) Cường độ dòng điện trong mạch chính là:

 \(I = \frac{{{E_1} + {E_2}}}{{{R_1} + {R_2}}} = \frac{{12 + 6}}{{4 + 8}} = 1,5A\)

b) Vì 2 điện trở ghép nối tiếp với nguồn

- Cường độ dòng điện

I₁ = I₂ = I = 1,5A

- Công suất tiêu thụ của điện trở :

P₁ = R₁. I₁² = 4. 1,52 = 9W

- Công suất tiêu thụ của điện trở 2:

P₂ = R₂ .I₂² = 8. 1,52 = 18W

c) Tính công suất và năng lượng

- Công suất của ắc quy 1:

P_acquy1 = E₁.I = 12. 1,5 = 18W

- Công suất của ắc quy 2:

P_acquy2 = E₂.I = 6. 1,5 = 9W

- Năng lượng của ắc quy 1 cung cấp trong 5 phút:

A_acquy1 = P_acquy1.t = 18.5.60 = 5400J

- Năng lượng của ắc quy 1 cung cấp trong 5 phút:

A_acquy2 = P_acquy2.t = 9.5.60 = 2700J

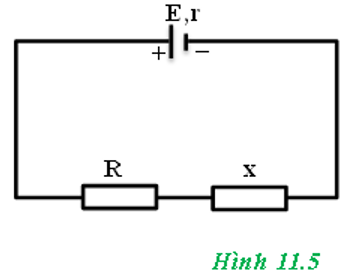
Cho mạch điện có sơ đồ như hình 11.5. Trong đó nguồn điện có suất điện động E = 12V và điện trở trong r = 1,1Ω; điện trở R = 0,1Ω.

a) Điện trở x phải có trị số là bao nhiêu để công suất tiêu thụ ở mạch ngoài là lớn nhất? Tính công suất lớn nhất đó.

b) Điện trở x phải có trị số là bao nhiêu để công suất tiêu thụ ở điện trở này là lớn nhất? Tính công suất lớn nhất đó.

Phương pháp giải

a) Áp dụng công thức:

P = R_N.I² để tính công suất tiêu thụ ở mạch ngoài

⇒ giá trị cực đại: P_max = E²/4r.

b) Áp dụng công thức:

P_x = R_x.I² để tính công suất tiêu thụ trên điện trở R_x

⇒ giá trị cực đại P_{x max} = E²/4(R+r)

Hướng dẫn giải

a) Công suất tiêu thụ ở mạch ngoài:

- Ta có: 

 \({P_N} = {R_N}.{I^2} = {R_N}.{(\frac{E}{{{R_N} + r}})^2}\)

\( = {E^2}/\)(\({R_N} + 2r + \)\(\frac{{{r^2}}}{{{R_N}}}\))

- Để công suất mạch ngoài cực đại (P_max)

⇒ mẫu số của biểu thức trên phải đạt cực tiểu tức :

\({({R_N} + 2r + \frac{{{r^2}}}{{{R_N}}})_{\min }}\)

- Áp dụng bất đẳng thức Cô-si cho 2 số dương R_N và r²/R_N

- Ta có: \({R_N} + 2r + \frac{{{r^2}}}{{{R_N}}} \ge 2r + 2\sqrt {{R_N}.(\frac{{{r^2}}}{{{R_N}}})} = 4r\)

- Dấu " = " xảy ra khi R_N = r

⇒ Rx = R_N – R = r – R = 1,1 – 0,1 = 1Ω

- Giá trị cực đại của công suất mạch ngoài:

 \({P_{N\max }} = \frac{{{E^2}}}{{4r}} = \frac{{{{12}^2}}}{{4.1,1}} = 32,73W\)

b) Công suất tiêu thụ trên điện trở Rx:

- Ta có:

 \({P_x} = {R_x}.{I^2} = {R_x}.{\left( {\frac{E}{{{R_x} + r + R}}} \right)^2} = \frac{{{E^2}}}{{{R_x} + 2(R + r) + \frac{{{{(R + r)}^2}}}{{{R_x}}}}}\)

- Áp dụng đẳng thức Cô-si cho hai số dương Rx và \(\frac{{(R + r){}^2}}{{{R_x}}}\)

- Ta có:

 \({R_x} + 2(R + r) + \frac{{{{(R + r)}^2}}}{{{R_x}}} \ge 2(R + r) + 2\sqrt {{R_x}.\frac{{(R + {r^2})}}{{{R_x}}}} = 4(R + r)\)

- Dấu " = " xảy ra khi R_x = R + r = 1,2Ω

- Giá trị cực đại của cống suất mạch ngoài:

 \({P_{x\,\,\max }} = \frac{{{E^2}}}{{4(R + r)}} = \frac{{{{12}^2}}}{{4.1,2}} = 30W\)