Bài 5: Sự co giãn của cầu cung

Các phân tích ở phần trên cho thấy, người tiêu dùng quyết định mua số lượng hàng hóa và dịch vụ với số lượng bao nhiêu là phụ thuộc vào giá của chính nó, thu nhập của họ, giá cả của các hàng hóa liên quan. Tuy nhiên, chúng ta không rõ tại sao một quyển sách giáo khoa đắt hơn một quyển tiểu thuyết nổi tiếng, tại sao giá gạo trên thị trường thế giới giảm tương đối so với các mặt hàng công nghiệp khác. Đo lường độ co giãn của cầu sẽ giúp chúng ta trả lời các câu hỏi này.

Độ co giãn của cầu đo lường sự phản ứng (hay sự nhạy cảm) của người tiêu dùng biểu hiện qua sự thay đổi lượng hàng được mua khi các yếu tố như giá cả hàng hóa, thu nhập, giá hàng liên quan thay đổi... Ở đây chúng ta xem xét ba loại độ co giãn:

(1) Độ co giãn của cầu theo giá (ED)

(2) Độ co giãn của cầu theo thu nhập EI)

(3) Độ co giãn chéo của cầu theo giá ( EXY )

Độ co giãn của cầu theo giá (ED) đo lường sự nhạy cảm của người tiêu dùng, biểu hiện qua sự thay đổi lượng cầu khi giá cả hàng hóa thay đổi.

Độ co giãn của cầu theo giá (ED) là tỉ lệ phần trăm thay đổi trong lượng cầu khi giá sản phẩm thay đổi một phần trăm (với điều kiện các yếu tố khác không đổi).

Công thức tính:

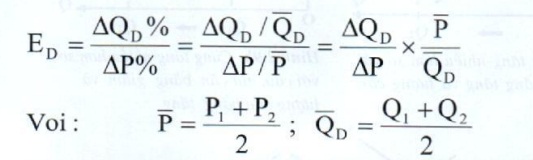   (2.3)

Trong đó, \(\Delta Q_D\) là sự thay đổi trong lượng cầu từ Q₁, đến Q₂: \(\Delta Q_D\) = Q₂ - Q₁; \(\Delta P\) là sự thay đổi của giá từ P₁ đến P₂: \(\Delta P\) = P₂ – P₁, như trong hình 2.10a. Khi độ co giãn được tính giữa hai điểm khác nhau trên đường cầu, nó được gọi là độ co giãn vòng cung hay độ co giãn khoảng.

Độ co giãn tính tại một điểm trên đường cầu đối với các thay đổi nhỏ trong giá cả là độ co giãn điểm, QD trong công thức là Q1 và P là P₁ . Độ co giãn điểm, nhất là đối với một đường cầu tuyến tính, có thể được tính toán đơn giản.

Công thức tính độ co giãn tại 1 điểm:

\(Ed = \frac{dQ}{dP}\times\frac{P}{Qd}\)          (2.4)

Tỷ số dQ / dP là hệ số góc (a) trong hàm cầu: Qn = aP + b,

 \(Ed = a \times \frac{P}{Q_D}\)            (2.5)

Nếu hàm số cầu có dạng P = f(Q) thì độ co giãn diểm được tính theo công thức:

 \(E_D = \frac{1}{\frac{dP}{dQ}} \times \frac{P}{Q_D}\)         (2.6)

Kỹ thuật tính toán này cũng có thể áp dụng để đo lường độ co giãn điểm trên một đường cầu cong. Giả sử độ co giãn được do tại A(P1,Q1), trong hình 2.10b. Đầu tiên kẻ tiếp tuyến với đường cầu tại A để xác định độ dốc (a) của đường cầu tại A, sau đó áp dụng công thức (2.5).

Ví dụ: Ta có hàm số cầu của sản phẩm X có dạng:

Qd = (-7/10)P + 42. Tính độ co giãn của cầu tại mức giá P = 40.

Tại P = 40 thì Qd = 14, hệ số co giãn của cầu tại mức giá P = 40:

 \(E_d = a \cdot \frac{P}{Q_d} = -\frac{7}{10} \cdot \frac{40}{14} = 2\) 

Hay hàm số cầu của sản phẩm X có dạng: P = -(10/7)Q + 60

Độ co giãn của cầu tại mức giá P = 40 và Qd = 14 là:

 \(E_d = \frac{1}{\frac{dP}{dQ}} \cdot \frac{P}{Q_D} = \frac{1}{-\frac{10}{7}} \cdot \frac{40}{14} = -2\) 

Chúng ta cũng có thể tính độ co giãn điểm bằng phương pháp hình học:

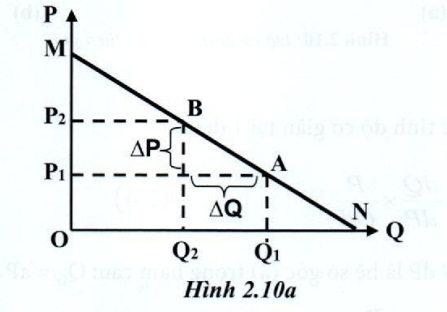
Trên đồ thị 2.10a, tính độ co giãn tại điểm B với mức giá là OP₂ = BQ₂ và lượng cầu là OQ₂.

Trên đồ thị 2.10a

 \(tg \alpha = \frac{\Delta P}{\Delta Q} = \frac{BQ_2}{Q_2N}\)      (5)

Độ co giãn tại điểm B

 \(E_D ={ \frac{\Delta Q}{\Delta P}} \cdot \frac{P}{Q}\)      (6)

Thế (5) và (6) ta có

 \(E_D = \frac{Q_2N}{BQ_2} \cdot \frac{OP_2}{OQ_2} = \frac{Q_2N}{BQ_2} \cdot \frac{BQ_2}{OQ_2}\) 

 \(E_D = \frac{Q_2N}{OQ_2}\)                     (7)

Theo tính chất của hình tam giác ta có:  \(\frac{Q_2N}{OQ_2} = \frac{BN}{BM} = \frac{OP_2}{P_2M}\)        (8)

Từ (7) và (8) ta có độ co giãn tại điểm B được tính:

 \(E_D = \frac{Q_2N}{OQ_2} = \frac{BN}{BM} = \frac{OP_2}{P_2M}\) 

Như vậy trên đồ thị, chúng ta có thể nhanh chóng xác định được độ co giãn của cầu theo giá tại bất kỳ điểm nào trên đường cầu, chẳng hạn độ co giãn của cầu theo giá tại điểm B trên đồ thị 2.10a được tính:

Xét trên trục hoành: bằng đọan sau chia cho đọan trước điểm B: ED=Q2N/OQ2.

Xét trên trục tung: bằng đọan dưới chia cho đọan trên điểm B: ED=OP2/P2M. Tính chất:

ED luôn luôn có giá trị âm, vì giá và lượng cầu thay đổi ngược chiều nhau. Nói chung, dấu của độ co giãn ít quan trọng đối với các nhà kinh tế hơn là qui mô của nó, do đó trong tính toán ta sử dụng trị tuyệt đối. Kết quả tính toán có thể xảy ra các trường hợp:

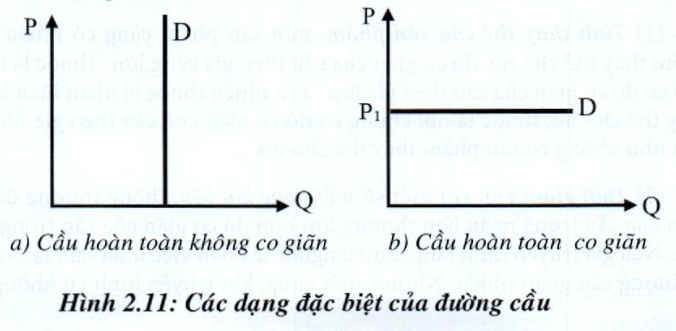
Nếu % \(\Delta Q_D\)  lớn hơn % \(\Delta P\) : người tiêu dùng phản ứng đáng kể đối với sự thay đổi của giá cả, giá trị của ED lớn hơn 1, ta nói cầu co giãn nhiều. Nếu % \(\Delta Q_D\)  nhỏ hơn % \(\Delta P\) : người tiêu dùng phản ứng nhẹ đối với sự thay đổi của giá cả, giá trị của ED nhỏ hơn 1, cầu co giãn ít. Nếu % \(\Delta Q_D\)  bằng % \(\Delta P\) , giá trị của ED bằng 1, cầu co giãn đơn vị Nếu % \(\Delta Q_D\)  rất nhỏ hay không đổi so với % \(\Delta P\) , giá trị của ED bằng 0, cầu hoàn toàn không co giãn. Trong trường hợp này đường cầu thẳng đứng, song song vớt trục giá cả (hình 2.11a). Muối ăn có thể là một ví dụ, nó là một loại hàng hóa mà những đơn vị đầu tiên là rất cần thiết. Tuy nhiên, mua nhiều hơn số lượng cần thiết sẽ trở nên rày rà. Do đó cho dù giá muối giảm cực thấp người tiêu dùng sẽ không mua nhiều hơn và họ cũng sẽ không mua ít hơn nếu giá tăng mạnh. Nếu % \(\Delta Q_D\)  vô hạn khi giá cả không thay đổi hay thay đổi rất ít, giá trị của ED bằng  \(\infty\) , cầu hoàn toàn co giãn.

Trong trường hợp này đường cầu nằm ngang, song song vớt trục số lượng (hình 2.11b). Đó là trường hợp đường cầu đối với các hãng trong thị trường cạnh tranh hoàn toàn.

Độ co giãn của cầu theo giá tác động đến tổng chi tiêu của người tiêu dùng và tổng doanh thu của các hãng kinh doanh Tổng chi tiêu của người tiêu dùng hay tổng doanh thu của hãng là tích số của giá bán và sản lượng: TR = P.Q

Khi cầu co giãn nhiều (ED> 1 hay ED < -1): % \(\Delta Q_D\)  lớn hơn % \(\Delta P\) , P & TR nghịch biến, do đó TR sẽ tăng khi giá giảm và TR sẽ giảm khi giá tăng.

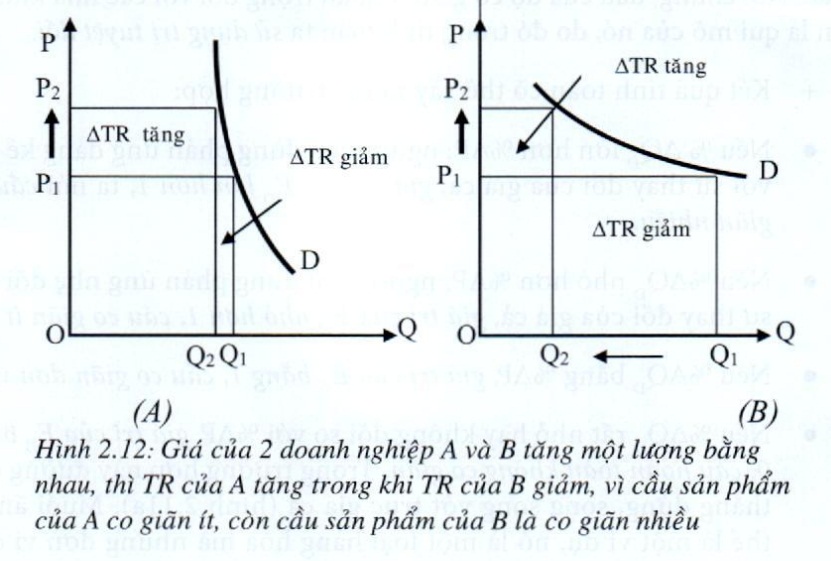
Khi cầu co giãn ít (ED<1, hay ED > -1): % \(\Delta Q_D\)  nhỏ hơn % \(\Delta P\) , P & TR đồng biến, do đó TR sẽ tăng khi giá tăng và TR sẽ giảm khi giá giảm. Khi cầu co giãn đơn vị (ED= 1): % \(\Delta Q_D\)  và % \(\Delta P\)  bằng nhau, P & TR độc lập, do đó khi giá thay đổi nhưng TR sẽ không đổi và đạt cực đại. Chúng ta có thể chứng minh mối quan hệ giữa mức giá (P) và tổng doanh thu (TR) bằng phương pháp đại số.

Các nhân tố tác động đến độ co giãn của cầu theo giá:

(1) Tính thay thế của sản phẩm: một sản phẩm càng có nhiều sản phẩm thay thế cho nó, độ co giãn của cầu theo giá càng lớn. Thuốc lá hiệu 555 có độ co giãn của cầu theo giá lớn vì có nhiều thuốc lá nhãn hiệu khác thay thế cho nó, thuốc lá nói chung có độ co giãn của cầu theo giá nhỏ vì hầu như không có sản phẩm thay thế cho nó.

(2) Thời gian: Đối với một số mặt hàng lâu bền, thông thường độ co giãn của cầu trong ngắn hạn thường lớn hơn độ co giãn của cầu trong dài hạn. Nếu giá truyền hình tăng, nhiều người sẽ hoãn việc mua sắm lại, và do đó lượng cầu giảm nhiều. Nhưng cuối cùng, khi truyền hình cũ không sử dụng được nữa và cần phải được thay thế, thì lượng cầu dài hạn sẽ không giảm nhiều như trong ngắn hạn.

Đối với các mặt hàng khác, thông thường độ co giãn của cầu trong ngắn hạn thường nhỏ hơn độ co giãn của cầu trong dài hạn. Một nguyên nhân là phải có thời gian người tiêu dùng mới có thể thay đổi thói quen tiêu dùng. Nếu giá cà phê tăng mạnh, lượng cầu cà phê sẽ giảm xuống dần dần, do người tiêu dùng bắt đầu bớt uống cà phê. Nguyên nhân khác là sự liên quan giữa các mặt hàng, ví dụ giá xăng tăng người tiêu dùng cùng không thể giảm lượng cầu nhiều ngay được, bởi vì phải có thời gian mới thay đổi xe ít tiêu hao nhiên liệu hơn, tính đến quãng đường đến sở làm khi thay đổi chỗ ở,...

(3) Tỷ phần chi tiêu của sản phẩm trong thu nhập: phần chi tiêu của sản phẩm chiếm tỷ trọng càng cao trong thu nhập của người tiêu thụ thì cầu của nó sẽ co giãn càng nhiều. Lượng cầu về khăn giấy giảm không bao nhiêu khi giá của nó tăng mạnh. Trong khi đó, nếu giá vé máy bay tăng mạnh thì lượng cầu về vé sẽ thay đổi đáng kể.

(4) Vị trí của mức giá trên đường cầu: độ co giãn của cầu theo giá thay đổi dọc theo đường cầu, mức giá càng cao thì cầu càng co giãn. Điều này có thể được giải thích đơn giản đối với đường cầu tuyến tính qua công thức (2.5) của độ co giãn. Giá trị a là một hằng số và theo qui luật cầu P càng lớn thì QD sẽ càng nhỏ, do đó:

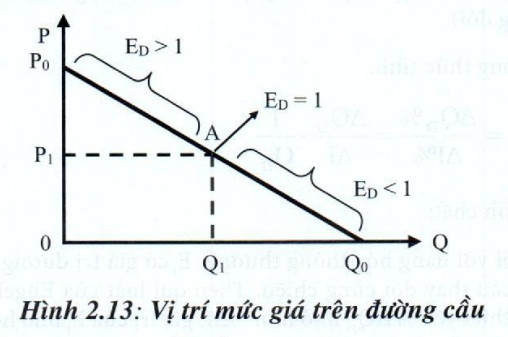
+ P = P₀ thì Q = 0, do đó  \(| E_D |\)  =  \(\infty\) 

+ P = 0 thì Q = Q₀, do đó  \(| E_D |\)  =0

+ P = P₁ thì Q = Q₁, do đó  \(| E_D |\)  = 1: cầu co giãn đơn vị

+ P₁ < P < P₀ thì  \(| E_D |\)  >1: cầu co giãn nhiều

+ O < P < P₁ thì  \(| E_D |\)  < 1: cầu co giãn ít

(5) Tính chất của sản phẩm: các mặt hàng thiết yếu có cầu ít co giãn hơn các mặt hàng xa xỉ. Giá gạo tăng người tiêu dùng sẽ không thể giảm lượng cầu về gạo nhiều, nhưng nếu giá mỹ phẩm hay nước hoa cao cấp tăng giá, phản ứng của họ sẽ thực sự đáng kể.

Ứng dụng ED:

Độ co giãn của cầu theo giá giúp chúng ta dự đoán giá và lượng cân bằng sẽ thay đổi như thế nào khi đường cung dịch chuyển:

Nếu cầu co giãn ít: đường cung dịch chuyển sẽ làm giá cân bằng thay đổi nhiều, còn lượng cân bằng thay đổi ít. Nếu cầu co giãn nhiều: đường cung dịch chuyển sẽ làm giá cân bằng thay đổi ít, còn lượng cân bằng thay đổi nhiều

Ví dụ: Nông sản thường có cẩu co giãn ít, nên khi mất mùa thì giá nông sản tăng lên đáng kể, còn lượng cân bằng giảm ít, thu nhập của nông dân sẽ tăng lên. Ngược lại, khi được mùa thì giá nông sản sẽ giảm nhiều, còn lượng cân bằng tăng ít, thu nhập của nông dân bị giảm xuống.

Độ co giãn của cầu theo thu nhập (EI) đo lường sự nhạy cảm của người tiêu dùng biểu hiện qua sự thay đổi lượng cầu khi thu nhập thay đổi.

Độ co giãn của cầu theo thu nhập (EI) là tỉ lệ phần trăm thay đổi trong lượng cầu khi thu nhập thay đổi một phần trăm (trong điều kiện các yếu tố khác không đổi).

Công thức tính:

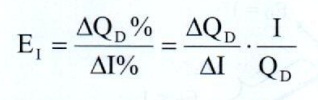               (2.7)

Ứng dụng EI:

Đối với hàng hóa thông thường, EI có giá trị dương, vì thu nhập và lượng cầu thay đổi cùng chiều. Theo qui luật của Engel, đối với các mặt hàng thiết yếu %  \(\Delta Q_D\)  nhỏ hơn % \(\Delta I\) , giá trị của EI nhỏ hơn 1. Đối với các hàng cao cấp, %  \(\Delta Q_D\)  lớn hơn % \(\Delta I\) , giá trị của EI lớn hơn 1. Đặc biệt đối với sản phẩm cấp thấp, EI có giá trị âm vì thu nhập và lượng cầu thay đổi ngược chiều.

Nghiên cứu độ co giãn của cầu theo thu nhập, sẽ giúp chúng ta dự đoán được mức độ thay đổi trong cầu của các hàng hoá và dịch vụ khi nền kinh tế tăng trưởng, khi mọi người trở nên khá giả hơn. Trên cơ sở này, sẽ giúp các nhà sản xuất xây dựng kế hoạch phát triển hàng hoá và dịch vụ cung ứng hợp lý.

Độ co giãn chéo của cầu theo giá (Exy) đo lường sự nhạy cảm của người tiêu dùng, biểu hiện qua sự thay đổi lượng cầu của một mặt hàng khi giá của mặt hàng liên quan với nó thay đổi.

Độ co giãn chéo của cầu theo giá (Exy) là tỷ lệ phần trăm thay đổi trong lượng cầu sản phẩm X khi giá sản phẩm Y thay đổi 1% (trong điều kiện các yếu tố khác không đổi).

Công thức tính:

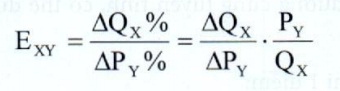               (2.8)

Tính chất:

Khi hai mặt hàng X và Y thay thế cho nhau được, EXY có giá trị dương (EXY > 0). Xăng A92 và xăng A95 có thể là ví dụ. Giá xăng A95 tăng có thể làm gia tăng sự tiêu thụ xăng A92 Khi X và Y là mặt hàng bổ sung lẫn nhau, EXY có giá trị âm (EXY < 0). Xăng và xe thường điển hình cho trường hợp này. Giá xăng tăng có thể làm giảm sự tiêu thụ xe. Khi X và Y là mặt hàng độc lập, EXY có giá trị bằng zero (EXY = 0). Ví dụ gạo và xe hơi. Giá xe hơi tăng không ảnh hưởng gì đến sự tiêu thụ gạo.

Khái niệm:

Độ co giãn của cung theo giá đo lường phản ứng của người sản xuất, biểu hiện qua sự thay đổi lượng hàng được cung ứng khi giá cả hàng hóa và dịch vụ thay đổi.

Độ co giãn của cung theo giá (Es) là tỉ lệ phần trăm thay đổi trong lượng cung khi giá sản phẩm thay đổi một phần trăm (với điều kiện các yếu tố khác không đổi).

Công thức tính:

                      (2.9)

Trong đó,  \(\Delta Q_S\)  là sự thay đổi trong lượng cung từ QS1 đến QS2 :  \(\Delta Q_S\)  = QS2 - QS1 :  \(\Delta P\)  là sự thay đổi giá từ P1 đến P2 :  \(\Delta P\)  = P2 - P1. Khi độ co giãn được tính giữa hai điểm khác nhau trên đường cung, nó được gọi là độ co giãn vòng cung, trong trường hợp này

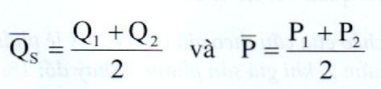
Độ co giãn tính tại một điểm trên đường cung đối với các thay đổi nhỏ trong giá cả là độ co giãn điểm, QS trong công thức là QS1 và P là P1. Độ co giãn điểm, nhất là đối với một đường cung tuyến tính, có thể được tính toán đơn giản.

Công thức tính độ co giãn tại 1 điểm:

 \(E_S = \frac{\Delta Q_S}{\Delta P} \times \frac{P}{Q_S}\)                                      (2.10)

Tương tự như cầu, tỷ số  \(\Delta Q_S\) / \(\Delta P\)  là hệ số góc (c) của hàm cung QS = c_P + d

 \(E_S = c \times \frac{P}{Q_S}\)                                              (2.11)

Ví dụ: Ta có hàm cung sản phẩm có dạng Q_S = (9/10P) - 6. Tính độ co giãn của cung tại mức giá P = 30.

Tại P = 30 thì Q = 21, và chúng ta tính được hệ số co giãn của cung tại mức giá P = 30:

 \(E_S = c \cdot \frac{P}{Q_S} = \frac{9}{10} \cdot \frac{30}{21} = 1.28\) 

Tính chất:

Es luôn luôn có giá trị dương, vì giá và lượng cung thay đổi cùng chiều nhau Tương tự như với cẩu, kết quả tính toán có thể xảy ra các trường hợp:

Nếu % \(\Delta Q_S\)  lớn hơn % \(\Delta P\) : người sản xuất phản ứng đáng kể đối với sự thay đổi của giá cả, ES > 1, cung co giãn nhiều. Nếu % \(\Delta Q_S\)  nhỏ hơn % \(\Delta P\) : người sản xuất phản ứng nhẹ đối với sự thay đổi của giá cả, ES < 1, cung ít co giãn. Nếu % \(\Delta Q_S\)  bằng % \(\Delta P\) , ES = 1, cung co giãn đơn vị. Nếu % \(\Delta Q_S\)  rất nhỏ hay không đổi so với % \(\Delta P\) , ES = 0, cung hoàn toàn không co giãn, nghĩa là cung của hàng hóa là một số lượng cố định bất kể giá cả như thế nào. Trong trường hợp này đường cung thẳng đủng, song song vớt trục giá cả, đường cung sản phẩm trong nhất thời là một ví dụ. Nếu % \(\Delta Q_S\)  vô hạn khi giá cả không thay đổi hay thay đổi rất ít, ES =  \(\infty\) , cung hoàn toàn co giãn. Trong trường hợp này đường cung nằm ngang, song song vớt trục số lượng, đường cung này hiếm có trong thực tế.

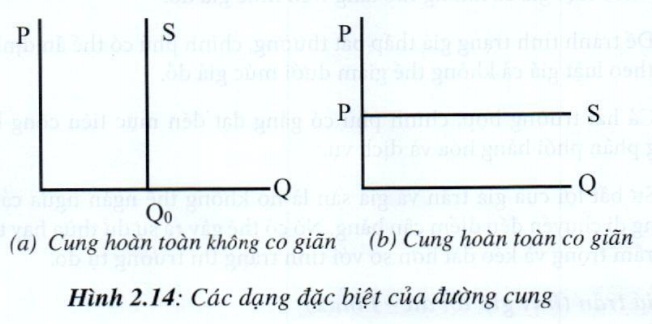
Các nhân tố tác động đến độ co giãn của cung theo giá:

Sự co giãn của cung theo giá phụ thuộc ở việc hãng có thể thay đổi lượng cung nhanh như thế nào khi giá thay đổi, có thể kể đến một vài nhân tố ảnh hưởng đến độ co giãn của cung:

(1) Thời gian sẽ ảnh hưởng đến việc tăng giảm các yếu tố sản xuất để tăng hay giảm năng lực sản xuất, để tham gia hay rút lui khỏi ngành. Thông thường đối với phần lớn sản phẩm, cung dài hạn co giãn nhiều hơn cung ngắn hạn, vì trong ngắn hạn công ty bị giới hạn năng lực sản xuất trong một qui mô sản xuất cố định.

(2) Khả năng dự trữ hàng hóa xác định liệu nó có thể được tồn trữ khi giá thấp và đưa ra thị trường khi giá cao hay không, Do đó, khả năng dự trữ xác định các công ty có thể thay đổi số lượng cung nhanh chóng như thế nào. 

Trên đây là nội dung bài giảng Bài 5: Sự co giãn của cầu cung được eLib tổng hợp lại nhằm giúp các bạn sinh viên có thêm tư liệu tham khảo!