Giải bài tập SBT Toán 12 Bài 6: Bất phương trình mũ và bất phương trình lôgarit
Để các em học sinh lớp 12 có thêm thật nhiều tài liệu ôn tập môn Toán, đội ngũ eLib đã biên soạn và tổng hợp nội dung giải bài tập bài Bất phương trình mũ và bất phương trình lôgarit SBT bên dưới đây. Tài liệu gồm 6 bài tập có phương pháp và đáp án chi tiết đi kèm sẽ giúp các em vừa làm bài vừa đối chiếu đáp án từ đó có kế hoạch học tập phù hợp cho bản thân.
Mục lục nội dung

1. Giải bài 2.59 trang 131 SBT Giải tích 12
Giải các bất phương trình mũ sau :
\(\begin{align} & a)\,{{3}^{\left| x-2 \right|}}<9; \\ & b)\,{{4}^{\left| x+1 \right|}}>16; \\ & c)\,{{2}^{-{{x}^{2}}+3x}}<4; \\ & d)\,{{\left( \dfrac{7}{9} \right)}^{2{{x}^{2}}-3x}}\ge \dfrac{9}{7}; \\ & e)\,{{11}^{\sqrt{x+6}}}\ge {{11}^{x}}; \\ & g)\,{{2}^{2x-1}}+{{2}^{2x-2}}+{{2}^{2x-3}}\ge 448; \\ & h)\,{{16}^{x}}-{{4}^{x}}-6\le 0; \\ & i)\dfrac{{{3}^{x}}}{{{3}^{x}}-2}<3. \\ \end{align} \)
Phương pháp giải
Đưa về cùng cơ số và sử dụng tính chất so sánh:
+ Nếu a > 1 thì \(\displaystyle {a^m} > {a^n} \Leftrightarrow m > n\)
+ Nếu 0 < a < 1 thì \(\displaystyle {a^m} > {a^n} \Leftrightarrow m < n\)
Hướng dẫn giải
\(\begin{aligned} & a) \\ & {{3}^{\left| x-2 \right|}}<9={{3}^{2}} \\ & \Leftrightarrow \left| x-2 \right|<2 \\ & \Leftrightarrow -2< x-2<2 \\ & \Leftrightarrow 0< x<4 \\ \end{aligned} \)
\(\begin{aligned} & b) \\ & {{4}^{\left| x+1 \right|}}>16={{4}^{2}} \\ & \Leftrightarrow \left| x+1 \right|>2 \\ & \Leftrightarrow \left[ \begin{aligned} & x+1<-2 \\ & x+1>2 \\ \end{aligned} \right. \\ & \Leftrightarrow \left[ \begin{aligned} & x<-3 \\ & x>1 \\ \end{aligned} \right. \\ \end{aligned} \)
\( \begin{aligned} & c) \\ & {{2}^{-{{x}^{2}}+3x}}<4={{2}^{2}} \\ & \Leftrightarrow -{{x}^{2}}+3x<2 \\ & \Leftrightarrow -{{x}^{2}}+3x-2<0 \\ & \Leftrightarrow \left[ \begin{aligned} & x<1 \\ & x>2 \\ \end{aligned} \right. \\ \end{aligned} \)
\( \begin{aligned} & d) \\ & {{\left( \dfrac{7}{9} \right)}^{2{{x}^{2}}-3x}}\ge \dfrac{9}{7}={{\left( \dfrac{7}{9} \right)}^{-1}} \\ & \Leftrightarrow 2{{x}^{2}}-3x\le -1 \\ & \Leftrightarrow 2{{x}^{2}}-3x+1\le 0 \\ & \Leftrightarrow x\in \left[ \dfrac{1}{2};1 \right] \\ \end{aligned} \)
\(\begin{aligned} & e)\,x\ge -6 \\ & {{11}^{\sqrt{x+6}}}\ge {{11}^{x}} \\ & \Leftrightarrow \sqrt{x+6}\ge x \\ \end{aligned} \)
+) Luôn đúng với \(x \in [-6;0]\)
+) Nếu \(x > 0\), ta có:
\(\begin{aligned} & x+6\ge {{x}^{2}} \\ & \Leftrightarrow {{x}^{2}}-x-6\le 0 \\ & \Leftrightarrow \left( x-3 \right)\left( x+2 \right)\le 0 \\ & \Leftrightarrow x\in \left[ -2;3 \right] \\ \end{aligned} \)
Vậy \(x\in \left[ -6;0 \right]\cup \left[ -2;3 \right] =[-6;3]\)
\(\begin{aligned} & g) \\ & {{2}^{2x-1}}+{{2}^{2x-2}}+{{2}^{2x-3}}\ge 448 \\ & \Leftrightarrow {{2}^{2x-3}}\left( {{2}^{2}}+2+1 \right)\ge 448 \\ & \Leftrightarrow {{2}^{2x-3}}\ge 64={{2}^{6}} \\ & \Leftrightarrow 2x-3\ge 6 \\ & \Leftrightarrow x\ge \dfrac{9}{2} \\ \end{aligned} \)
\(\begin{aligned} & h)\, \\ & {{16}^{x}}-{{4}^{x}}-6\le 0 \\ & \Leftrightarrow {{4}^{2x}}-{{4}^{x}}-6\le 0 \\ & \Leftrightarrow \left( {{4}^{x}}-3 \right)\left( {{4}^{x}}+2 \right)\le 0 \\ & \Leftrightarrow {{4}^{x}}-3\le 0\,\,\,\,\,\,\,\,\left( \text{vì}\,\,{{4}^{x}}+2>0\,\,\,\forall x \right) \\ & \Leftrightarrow x\le {{\log }_{4}}3 \\ \end{aligned} \)
\(\begin{aligned} & i) \\ & \dfrac{{{3}^{x}}}{{{3}^{x}}-2}<3 \\ & \Leftrightarrow \dfrac{{{3}^{x}}}{{{3}^{x}}-2}-3<0 \\ & \Leftrightarrow \dfrac{{{3}^{x}}-3\left( {{3}^{x}}-2 \right)}{{{3}^{x}}-2}<0 \\ & \Leftrightarrow \dfrac{-{{2.3}^{x}}+6}{{{3}^{x}}-2}<0 \\ & \Leftrightarrow \left[ \begin{aligned} & {{3}^{x}}>3 \\ & {{3}^{x}}<2 \\ \end{aligned} \right.\Leftrightarrow \left[ \begin{aligned} & x>1 \\ & x<{{\log }_{3}}2 \\ \end{aligned} \right. \\ \end{aligned} \)
2. Giải bài 2.60 trang 132 SBT Giải tích 12
Giải các bất phương trình lôgarit sau :
\(\begin{align} & a)\,{{\log }_{\frac{1}{3}}}\left( x-1 \right)\ge -2; \\ & b)\,{{\log }_{3}}\left( x-3 \right)+{{\log }_{3}}\left( x-5 \right)<1; \\ & c)\,{{\log }_{\frac{1}{2}}}\dfrac{2{{x}^{2}}+3}{x-7}<0; \\ & d)\,{{\log }_{\frac{1}{3}}}{{\log }_{2}}{{x}^{2}}>0; \\ & e)\dfrac{1}{5-\log x}+\dfrac{2}{1+\log x}<1; \\ & g)4{{\log }_{4}}x-33{{\log }_{x}}4\le 1. \\ \end{align} \)
Phương pháp giải
Biến đổi bất phương trình dạng cơ bản và sử dụng so sánh logarit:
+ Nếu \(\displaystyle 0 < a < 1\) thì \(\displaystyle {\log _a}f\left( x \right) > {\log _a}g\left( x \right)\) \(\displaystyle \Leftrightarrow f\left( x \right) < g\left( x \right)\).
+ Nếu \(\displaystyle a > 1\) thì \(\displaystyle {\log _a}f\left( x \right) > {\log _a}g\left( x \right)\) \(\displaystyle \Leftrightarrow f\left( x \right) > g\left( x \right)\).
Hướng dẫn giải
a) ĐK : \( x > 1\)
\(\begin{aligned} & {{\log }_{\frac{1}{3}}}\left( x-1 \right)\ge -2 \\ & \Leftrightarrow -{{\log }_{3}}\left( x-1 \right)\ge -2 \\ & \Leftrightarrow {{\log }_{3}}\left( x-1 \right)\le 2 \\ & \Leftrightarrow x-1\le {{3}^{2}} \\ & \Leftrightarrow x\le 10 \\ \end{aligned}\)
Vậy \(x\in (1;10] \)
b) ĐK: \(x>5 \)
\(\begin{aligned} & {{\log }_{3}}\left( x-3 \right)+{{\log }_{3}}\left( x-5 \right)<1 \\ & \Leftrightarrow {{\log }_{3}}\left[ \left( x-3 \right)\left( x-5 \right) \right]<1 \\ & \Leftrightarrow {{x}^{2}}-8x+15<3 \\ & \Leftrightarrow {{x}^{2}}-8x+12<0 \\ & \Leftrightarrow 2< x<6 \\ \end{aligned} \)
Kết hợp điều kiện, suy ra \(5< x<6 \)
c) ĐK: \(x>7 \)
\(\begin{aligned} & {{\log }_{\frac{1}{2}}}\dfrac{2{{x}^{2}}+3}{x-7}<0 \\ & \Leftrightarrow \dfrac{2{{x}^{2}}+3}{x-7}>1 \\ & \Leftrightarrow \dfrac{2{{x}^{2}}+3}{x-7}-1>0 \\ & \Leftrightarrow \dfrac{2{{x}^{2}}-x+10}{x-7}>0 \\ & \Leftrightarrow \dfrac{{{x}^{2}}+{{x}^{2}}-x+1+9}{x-7}>0 \\ & \Leftrightarrow x-7>0 \\ & \Leftrightarrow x>7 \\ \end{aligned} \)
Vậy x> 7
d) ĐK: \(x\in \mathbb{R} \)
\(\begin{aligned} & {{\log }_{\frac{1}{3}}}{{\log }_{2}}{{x}^{2}}>0 \\ & \Leftrightarrow \left\{ \begin{aligned} & {{\log }_{2}}{{x}^{2}}>0 \\ & {{\log }_{2}}{{x}^{2}}<1 \\ \end{aligned} \right. \\ & \Leftrightarrow \left\{ \begin{aligned} & {{x}^{2}}>1 \\ & {{x}^{2}}<2 \\ \end{aligned} \right. \\ & \Leftrightarrow \left\{ \begin{aligned} & \left[ \begin{aligned} & x<-1 \\ & x>1 \\ \end{aligned} \right. \\ & -\sqrt{2}< x<\sqrt{2} \\ \end{aligned} \right.\Leftrightarrow x\in \left( -\sqrt{2};-1 \right)\cup \left( 1;\sqrt{2} \right) \\ \end{aligned} \)
e) ĐK \(x> 0; x\ne {{10}^{5}};x\ne \dfrac{1}{10} \)
\(\begin{aligned} & \dfrac{1}{5-\log x}+\dfrac{2}{1+\log x}<1 \\ & \Leftrightarrow \dfrac{1+\log x+2\left( 5-\log x \right)-\left( 5-\log x \right)\left( 1+\log x \right)}{\left( 5-\log x \right)\left( 1+\log x \right)}<0 \\ & \Leftrightarrow \dfrac{{{\log }^{2}}x-5\log x+6}{\left( 5-\log x \right)\left( 1+\log x \right)}<0 \\ & \Leftrightarrow \dfrac{\left( \log x-2 \right)\left( \log x-3 \right)}{\left( 5-\log x \right)\left( 1+\log x \right)}<0 \\ & \Leftrightarrow \left[ \begin{aligned} & \log x<-1 \\ & 2<\log x<3 \\ & \log x>5 \\ \end{aligned} \right. \\ & \Leftrightarrow \left[ \begin{aligned} & x<\dfrac{1}{10} \\ & 100< x<1000 \\ & x>{{10}^{5}} \\ \end{aligned} \right. \\ \end{aligned}\)
Kết hợp điều kiện, ta có:
\(\left[ \begin{aligned} & 0< x<\dfrac{1}{10} \\ & 100< x<1000 \\ & x>100000 \\ \end{aligned} \right. \)
g) ĐK: \(x> 0\)
\(\begin{aligned} & 4{{\log }_{4}}x-33{{\log }_{x}}4\le 1 \\ & \Leftrightarrow 4{{\log }_{4}}x-\dfrac{33}{{{\log }_{4}}x}-1\le 0 \\ & \Leftrightarrow \dfrac{4\log _{4}^{2}x-{{\log }_{4}}x-33}{{{\log }_{4}}x}\le 0 \\ & \Leftrightarrow \left[ \begin{aligned} & {{\log }_{4}}x\le -\dfrac{11}{4} \\ & 0<{{\log }_{4}}x\le 3 \\ \end{aligned} \right. \\ & \Leftrightarrow \left[ \begin{aligned} & x\le {{4}^{-\frac{11}{4}}} \\ & 1< x<{{4}^{3}} \\ \end{aligned} \right. \\ \end{aligned} \)
Kết hợp điều kiện, ta có: \(\left[ \begin{aligned} & 0 < x\le {{4}^{-\frac{11}{4}}} \\ & 1< x\le 64 \\ \end{aligned} \right. \)
3. Giải bài 2.61 trang 132 SBT Giải tích 12
Giải các bất phương trình sau bằng đồ thị
\( \begin{align} & a)\,{{\left( \dfrac{1}{2} \right)}^{x}}< x-\dfrac{1}{2}; \\ & b)\,{{\left( \dfrac{1}{3} \right)}^{x}}\ge x+1; \\ & c)\,{{\log }_{\frac{1}{3}}}x >3x; \\ & d)\,{{\log }_{2}}x\le 6-x \\ \end{align} \)
Phương pháp giải
- Vẽ đồ thị hàm số\(\displaystyle y = {\left( {\frac{1}{2}} \right)^x}\left( C \right)\) và đường thẳng \(\displaystyle y = x - \frac{1}{2}\left( d \right)\) trên cùng một mặt phẳng tọa độ.
- Quan sát đồ thị, nghiệm của bất phương trình là phần x mà ứng với nó thì đồ thị (C) nằm phía dưới đường thẳng d
Hướng dẫn giải
a)
Vẽ đồ thị hàm số \(y=\left(\dfrac 1 2 \right)^x\) và \(y=x-\dfrac 1 2\) trên cùng một hệ tọa độ ta được:
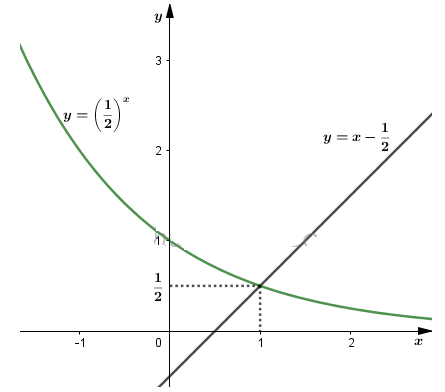
Do vậy \(\,{{\left( \dfrac{1}{2} \right)}^{x}}< x-\dfrac{1}{2}\Leftrightarrow x > 1\)
b)
Vẽ đồ thị hàm số \(y=\left(\dfrac 1 3 \right)^x\) và \(y=x+1\) trên cùng một hệ tọa độ ta được:
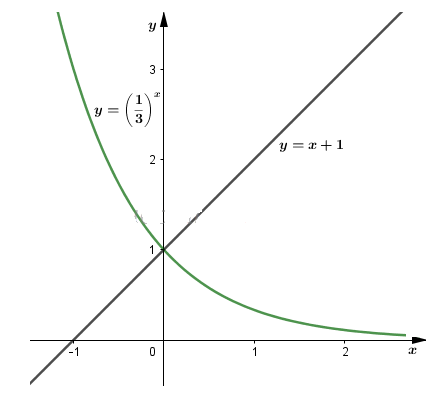
Từ đồ thị hàm số, ta có: \({{\left( \dfrac{1}{3} \right)}^{x}}\ge x+1\Rightarrow x\le 0\)
c)
Vẽ đồ thị hàm số \(y={{\log }_{\frac{1}{3}}}x \) và \(y=3x\) trên cùng một hệ tọa độ ta được:
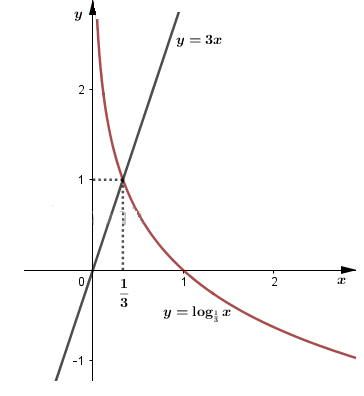
Từ đồ thị hàm số, ta có: \({{\log }_{\frac{1}{3}}}x >3x\Rightarrow 0 < x < \dfrac 1 3\)
d)
Vẽ đồ thị hàm số \(y={{\log }_{2}}x \) và \(y=6-x\) trên cùng một hệ tọa độ ta được:
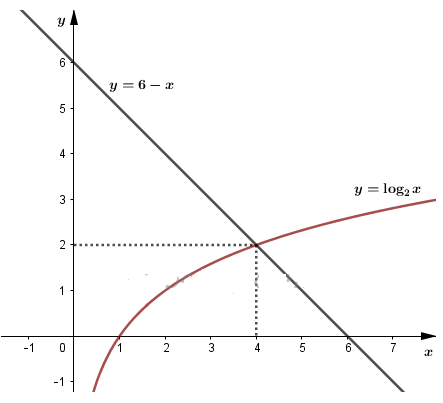
Từ đồ thị hàm số, ta có: \(\log_2x\le 6-x\Rightarrow 0< x\le 4\)
4. Giải bài 2.62 trang 132 SBT Giải tích 12
Tìm tập hợp nghiệm của bất đẳng thức \(\left(\dfrac 1 2 \right)^{\frac 1 x}\ge \left(\dfrac 1 2 \right)^4\)
A. \((-\infty;0)\)
B. \(\left(\dfrac 1 4 ;+\infty\right)\)
C. \((-\infty;0)\cup \left(\dfrac 1 4 ;+\infty \right)\)
D. \((-\infty;0)\cup \left[\dfrac 1 4 ;+\infty\right)\)
Phương pháp giải
Sử dụng so sánh \(\displaystyle {a^m} > {a^n} \Leftrightarrow m < n\) nếu 0 < a < 1
Hướng dẫn giải
\(\begin{aligned} & {{\left( \dfrac{1}{2} \right)}^{\frac{1}{x}}}\ge {{\left( \dfrac{1}{2} \right)}^{4}} \\ & \Leftrightarrow \dfrac{1}{x}\le 4 \\ & \Leftrightarrow \dfrac{1}{x}-4\le 0 \\ & \Leftrightarrow \dfrac{1-4x}{x}\le 0 \\ & \Leftrightarrow \left[ \begin{aligned} & x<0 \\ & x\ge \dfrac{1}{4} \\ \end{aligned} \right. \\ \end{aligned} \)
Chọn D.
5. Giải bài 2.63 trang 132 SBT Giải tích 12
Tìm \(x\), biết \(\lg2x<1\)
A. \(x> 5\)
B. \(0< x< 5\)
C. \(x> 10\)
D. \(0< x< 10\)
Phương pháp giải
Sử dụng phương pháp giải phương trình logarit cơ bản \(\displaystyle {\log _a}f\left( x \right) < m \Leftrightarrow f\left( x \right) < {a^m} \,\, với \,\,\displaystyle a > 1\)
Hướng dẫn giải
\(\begin{align} & \lg 2x<1 \\ & \Leftrightarrow 0< 2x<10 \\ & \Leftrightarrow 0< x<5 \\ \end{align} \)
Chọn B
6. Giải bài 2.64 trang 132 SBT Giải tích 12
Tìm tập hợp nghiệm của bất phương trình \(\log_3 \dfrac{2x}{x+1}>1\)
A. \((-\infty;-3)\)
B. \((-1;+\infty)\)
C. \((-\infty;-3)\cup(-1;+\infty)\)
D. \((-3;-1)\)
Phương pháp giải
Sử dụng phương pháp giải phương trình logarit cơ bản \(\displaystyle {\log _a}f\left( x \right) < m \Leftrightarrow f\left( x \right) < {a^m} \,\, với \,\,\displaystyle a > 1\)
Hướng dẫn giải
\(\begin{aligned} & {{\log }_{3}}\dfrac{2x}{x+1}>1 \\ & \Leftrightarrow \left\{ \begin{aligned} & \dfrac{2x}{x+1}>0 \\ & \dfrac{2x}{x+1}>3 \\ \end{aligned} \right. \\ & \Leftrightarrow \left\{ \begin{aligned} & \left[ \begin{aligned} & x<-1 \\ & x>0 \\ \end{aligned} \right. \\ & \dfrac{2x}{x+1}-3>0 \\ \end{aligned} \right. \\ & \Leftrightarrow \left\{ \begin{aligned} & \left[ \begin{aligned} & x<-1 \\ & x>0 \\ \end{aligned} \right. \\ & \dfrac{-x-3}{x+1}>0 \\ \end{aligned} \right. \\ & \Leftrightarrow \left\{ \begin{aligned} & \left[ \begin{aligned} & x<-1 \\ & x>0 \\ \end{aligned} \right. \\ & -3< x<-1 \\ \end{aligned} \right.\Leftrightarrow -3< x<-1 \\ \end{aligned} \)
Chọn D
Các em hãy luyện tập bài trắc nghiệm Bất phương trình mũ và bất phương trình lôgarit Toán 12 sau để nắm rõ thêm kiến thức bài học.
