Giải bài tập SBT Toán 12 Bài 1: Khái niệm về mặt tròn xoay
Nhằm giúp các em học sinh lớp 12 học thật tốt môn Toán, eLib đã biên soạn và tổng hợp nội dung giải 12 bài tập SBT từ trang 46, 47, 48. Thông qua tài liệu này các em sẽ định hướng được phương pháp giải đồng thời tự đánh giá được năng lực bản thân để có kế hoạch ôn tập phù hợp, hiệu quả. Mời các em cùng theo dõi nội dung chi tiết.
Mục lục nội dung
1. Giải bài 2.1 trang 46 SBT Hình học 12
2. Giải bài 2.2 trang 47 SBT Hình học 12
3. Giải bài 2.3 trang 47 SBT Hình học 12
4. Giải bài 2.4 trang 47 SBT Hình học 12
5. Giải bài 2.5 trang 47 SBT Hình học 12
6. Giải bài 2.6 trang 47 SBT Hình học 12
7. Giải bài 2.7 trang 47 SBT Hình học 12
8. Giải bài 2.8 trang 47 SBT Hình học 12
9. Giải bài 2.9 trang 47 SBT Hình học 12
10. Giải bài 2.10 trang 48 SBT Hình học 12

1. Giải bài 2.1 trang 46 SBT Hình học 12
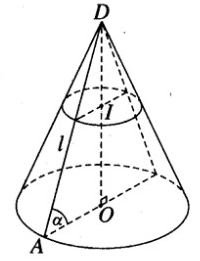
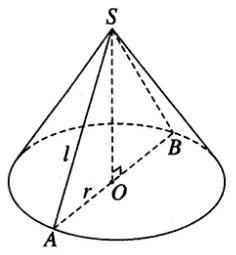
Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng α
a) Tính diện tích xung quanh của hình nón và thể tích khối nón được tạo nên.
b) Gọi I là một điểm trên đường cao DO của hình nón sao cho \(\dfrac{{DI}}{{DO}} = k(0 < k < l)\). Tính diện tích thiết diện qua I và vuông góc với trục của hình nón.
Phương pháp giải
a) Áp dụng các công thức: \({S_{xq}} = \pi rl \,\,và \,\, V = \dfrac{1}{3}\pi {r^2}h\)
b) Xác định tâm và bán kính của thiết diện (hình tròn), tính diện tích theo công thức \(S = \pi {R^2}\)
Hướng dẫn giải
a) Gọi r là bán kính của đường tròn đáy.
Ta có \(OA{\rm{ }} = {\rm{ }}r{\rm{ }} = l.\cos \alpha\) (với O là tâm của đường tròn đáy và A là một điểm trên đường tròn đó).
Ta suy ra: \({S_{xq}} = \pi rl = \pi {l^2}\cos \alpha\)
Khối nón có chiều cao \(h = DO = l\sin \alpha\). Do đó thể tích V của khối nón được tính theo công thức \(V = \dfrac{1}{3}Bh = \dfrac{1}{3}\pi {r^2}.h\)
Vậy : \(V = \dfrac{1}{3}\pi {l^2}{\cos ^2}\alpha .l\sin \alpha = \dfrac{1}{3}\pi {l^3}{\cos ^2}\alpha \sin \alpha \)
b) Thiết diện qua I và vuông góc với trục hình nón là một hình tròn bán kính r’ với \(\dfrac{{r'}}{r} = \dfrac{{DI}}{{DO}} = k \Rightarrow r' = kr = k.l\cos \alpha\)
Vậy diện tích của thiết diện đi qua điểm I và vuông góc với trục hình nón là: \(S = \pi r{'^2} = \pi {k^2}{l^2}{\cos ^2}\alpha\)
2. Giải bài 2.2 trang 47 SBT Hình học 12
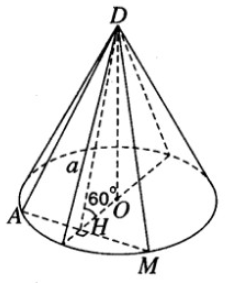
Một hình nón tròn xoay có thiết diện qua trục là một tam giác vuông cân có cạnh bằng a.
a) Tính diện tích toàn phần và thể tích hình nón đó.
b) Một mặt phẳng đi qua đỉnh tạo với mặt phẳng đáy một góc 60o. Tính diện tích thiết diện được tạo nên.
Phương pháp giải
a) Sử dụng các công thức \({S_{tp}} = {S_{xq}} + {S_d} = \pi rl + \pi {r^2}\,\, và \,\,V = \dfrac{1}{3}\pi {r^2}h\).
b) Xác định góc \({60^0}\) (góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng cùng vuông góc giao tuyến).
Tính diện tích theo công thức \(S = \dfrac{1}{2}dh\) với d là độ dài cạnh đáy tam giác, h là chiều cao
Hướng dẫn giải
a) Thiết diện qua trục của hình nón là tam giác vuông cân cạnh a nên hình nón có đường sinh l = a, có đường kính đáy \(a\sqrt 2\) nên bán kính đáy \(r = \dfrac{{a\sqrt 2 }}{2}\), và có chiều cao \(h = r = \dfrac{{a\sqrt 2 }}{2}\)
Gọi \({S_{xq}}\) là diện tích xung quanh của hình nón, ta có: \({S_{xq}} = \pi rl = \pi \dfrac{{a\sqrt 2 }}{2}.a = \dfrac{{\pi {a^2}\sqrt 2 }}{2}\)
Gọi S là diện tích đáy của hình nón, ta có \({S_d} = \pi {r^2} = \dfrac{{\pi {a^2}}}{2}\)
Vậy diện tích toàn phần của hình nón đã cho là:
\({S_{tp}} = {S_{xq}} + {S_d}\)\( = \dfrac{1}{2}\pi {a^2}\sqrt 2 + \dfrac{1}{2}\pi {a^2}\) \( = \dfrac{1}{2}\pi {a^2}\left( {\sqrt 2 + 1} \right)\)
Hình nón có thể tích là: \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^2}.\dfrac{{a\sqrt 2 }}{2}= \dfrac{1}{{12}}\pi {a^3}\sqrt 2 \)
b) Xét mặt phẳng (DAM) đi qua đỉnh D tạo với mặt phẳng đáy một góc \({60^0}\), cắt đường tròn đáy tại hai điểm A và M.
Từ tâm O của đường tròn đáy ta vẽ \(OH \bot AM\), do vậy H là trung điểm của đoạn AM. Ta có \(AM \bot (DOH)\) vì \(AM \bot OH\) và \(AM \bot DO\)
Vậy \(\widehat {DHO} = {60^0} \,\, và \,\, \sin {60^0} = \dfrac{{DO}}{{DH}} \,\, hay \,\,DH = \dfrac{{DO}}{{\sin {{60}^0}}} = \dfrac{{a\sqrt 2 }}{2}:\dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt 2 }}{{\sqrt 3 }}\)
Gọi \({S_{\Delta DAM}}\) là diện tích thiết diện cần tìm, ta có: \({S_{\Delta DAM}} = \dfrac{1}{2}AM.DH = AH.DH\)
Mà
\(A{H^2} = D{A^2} - D{H^2}\)\( = {a^2} - \dfrac{{2{a^2}}}{3} = \dfrac{{{a^2}}}{3}\) \( \Rightarrow AH = \dfrac{a}{{\sqrt 3 }}\)
Vậy \({S_{\Delta DAM}} = AH.DH = \dfrac{a}{{\sqrt 3 }}.\dfrac{{a\sqrt 2 }}{{\sqrt 3 }} = \dfrac{{{a^2}\sqrt 2 }}{3}\)
3. Giải bài 2.3 trang 47 SBT Hình học 12
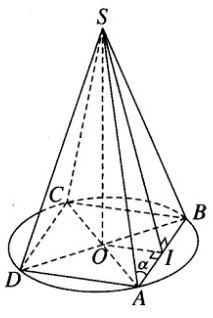
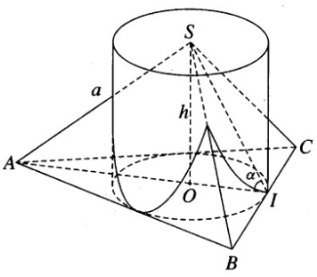
Cho S.ABC là hình chóp tam giác đều có các cạnh bên bằng a và có góc giữa các mặt bên và mặt phẳng đáy là α. Hình nón đỉnh S có đường tròn đáy nội tiếp tam giác đều ABC gọi là hình nón nội tiếp hình nón đã cho. Hãy tính diện tích xung quanh của hình nón này theo a và α .
Phương pháp giải
Sử dụng công thức tính diện tích xung quanh \({S_{xq}} = \pi rl.\)
Hướng dẫn giải
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC.
Theo giả thiết ta có SA = SB = SC = a và \(\widehat {SIO} = \alpha\)
Đặt OI = r, SO = h, ta có AO = 2r và \(\left\{ {\begin{array}{*{20}{c}}{h = r\tan \alpha }\\{{a^2} = {h^2} + 4{r^2}}\end{array}} \right.\) (vì \(S{A^2} = {\rm{ }}S{O^2} + {\rm{ }}A{O^2}\))
Do đó \({a^2} = {r^2}{\tan ^2}\alpha + 4{r^2} = {r^2}({\tan ^2}\alpha + 4)\)
Vậy \(r = \dfrac{a}{{\sqrt {{{\tan }^2}\alpha + 4} }}\)
Hình nón nội tiếp có đường sinh là: \(l = SI = \dfrac{r}{{\cos \alpha }} = \dfrac{a}{{\cos \alpha \sqrt {{{\tan }^2}\alpha + 4} }}\)
Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là:
\({S_{xq}} = \pi rl\)\( = \pi .\dfrac{a}{{\sqrt {{{\tan }^2}\alpha + 4} }}.\dfrac{a}{{\cos \alpha \sqrt {{{\tan }^2}\alpha + 4} }}\) \( = \dfrac{{\pi {a^2}}}{{\cos \alpha ({{\tan }^2}\alpha + 4)}}\)
4. Giải bài 2.4 trang 47 SBT Hình học 12
Cho hình chóp tứ giác đều S.ABCD có chiều cao SO = h và góc \(\widehat {SAB} = \alpha (\alpha > {45^0})\). Tính diện tích xung quanh của hình nón đỉnh S và có đường tròn đáy ngoại tiếp hình vuông ABCD của hình chóp.
Phương pháp giải
Sử dụng công thức \({S_{xq}} = \pi rl\)
Hướng dẫn giải
Gọi r là bán kính đáy của hình nón ta có OA = r, SO = h và SA = SB = SC = SD =l là đường sinh của hình nón.
Gọi I là trung điểm của đoạn AB, ta có:
\(\left\{ \begin{array}{l}S{A^2} = S{O^2} + O{A^2}\\AI = SA.\cos \alpha \end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{l^2} = {h^2} + {r^2}(1)\\\dfrac{{r\sqrt 2 }}{2} = l\cos \alpha (2)\end{array} \right.\)
\((2) \Rightarrow r = \sqrt 2 l\cos \alpha\)
\((1) \Rightarrow {l^2} = {h^2} + 2{l^2}{\cos ^2}\alpha \)\( \Rightarrow {h^2} = {l^2}(1 - 2{\cos ^2}\alpha )\) \( \Rightarrow {l^2} = \dfrac{{{h^2}}}{{1 - 2{{\cos }^2}\alpha }}\) \( \Rightarrow l = \dfrac{h}{{\sqrt {1 - 2{{\cos }^2}\alpha } }}\)
Do đó \(r = \sqrt 2 l\cos \alpha = \dfrac{{\sqrt 2 h\cos \alpha }}{{\sqrt {1 - 2{{\cos }^2}\alpha } }}\)
\({S_{xq}} = \pi rl\)\( = \pi .\dfrac{{\sqrt 2 h\cos \alpha }}{{\sqrt {1 - 2{{\cos }^2}\alpha } }}.\dfrac{h}{{\sqrt {1 - 2{{\cos }^2}\alpha } }}\) \( = \dfrac{{\pi \sqrt 2 {h^2}\cos \alpha }}{{1 - 2{{\cos }^2}\alpha }}\)
5. Giải bài 2.5 trang 47 SBT Hình học 12
Chứng minh rằng trong một khối nón tròn xoay, góc ở đỉnh là góc lớn nhất trong số các góc được tạo nên bởi hai đường sinh của khối nón đó.
Phương pháp giải
Sử dụng tính chất góc và cạnh đối diện trong tam giác.
Hướng dẫn giải
Xét hai đường sinh SA , SB tùy ý của hình nón. Vẽ đường kính AC của đường tròn đáy. Ta có góc ASC là góc ở đỉnh của hình nón.
Hai tam giác ASC và ASB có hai cặp cạnh bằng nhau vì chúng cùng là đường sinh của hình nón.
Ta có cạnh \(AC \ge AB\) nên \(\widehat {{\rm{AS}}C} \ge \widehat {ASB}\)
Đó là điều cần chứng minh.
6. Giải bài 2.6 trang 47 SBT Hình học 12
Cho khối nón có bán kính đáy r = 12 cm và có góc ở đỉnh là α = 120o. Hãy tính diện tích của thiết diện đi qua hai đường sinh vuông góc với nhau.
Phương pháp giải
- Tính độ dài đường sinh của khối nón.
- Tính diện tích tam giác vuông và kết luận.
Hướng dẫn giải
Theo giả thiết ta có góc ở đỉnh của hình nón là \(\displaystyle \widehat {ASB} = \alpha = {120^0}\)
Gọi O là tâm của đường tròn đáy. Ta có: \(\displaystyle \widehat {ASO} = {60^0}\) và \(\displaystyle \sin {60^0} = {{OA} \over {SA}} = {r \over l}\) với l là độ dài đường sinh của hình nón.
Vậy \(\displaystyle l = {r \over {\sin {{60}^0}}} = {{12} \over {{{\sqrt 3 } \over 2}}} = {{24} \over {\sqrt 3 }}\)
Khi có hai đường sinh vuông góc với nhau ta có tam giác vuông có diện tích là \(\displaystyle {1 \over 2}{l^2}\).
Do đó, diện tích của thiết diện là: \(\displaystyle S = {1 \over 2}{l^2} \displaystyle = {1 \over 2}.{{{{24}^2}} \over 3}\displaystyle = 96(c{m^2}\)
7. Giải bài 2.7 trang 47 SBT Hình học 12
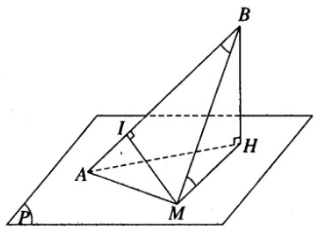
Cho mặt phẳng (P). Gọi A là một điểm nằm trên (P) và B là một điểm nằm ngoài (P) sao cho hình chiếu H của B trên (P) không trùng với A. Một điểm M chạy trên mặt phẳng (P) sao cho góc \(\widehat {ABM} = \widehat {BMH}\). Chứng minh rằng điểm M luôn luôn nằm trên một mặt trụ xoay có trục là AB.
Phương pháp giải
Gọi I là hình chiếu của M lên AB. Chứng minh MI=BH không đổi và suy ra khối trụ cần tìm.
Hướng dẫn giải
Giải sử ta có điểm M thuộc mặt phẳng (P) thỏa mãn các điều kiện của giả thiết đã cho.
Gọi I là hình chiếu vuông góc của M trên AB. Hai tam giác vuông BIM và MHB bằng nhau vì có cạnh huyền chung và một cặp góc nhọn bằng nhau.
Do đó MI = BH không đổi. Vậy điểm M luôn luôn nằm trên mặt trụ trục AB và có bán kính bằng BH.
8. Giải bài 2.8 trang 47 SBT Hình học 12
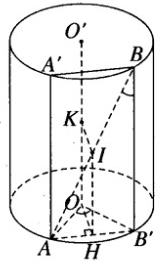
Cho mặt trụ tròn xoay \((\Im )\) và một điểm S cố định nằm ngoài \((\Im )\). Một đường thẳng d thay đổi luôn luôn đi qua S cắt \((\Im )\) tại A và B. Chứng minh rằng trung điểm I của đoạn thẳng AB luôn luôn nằm trên một mặt trụ xác định.
Phương pháp giải
Gọi A', B', I' lần lượt là hình chiếu của A, B, I trên mặt phẳng (P). Tìm quỹ tích của đường thẳng II' rồi suy ra quỹ tích điểm I.
Hướng dẫn giải
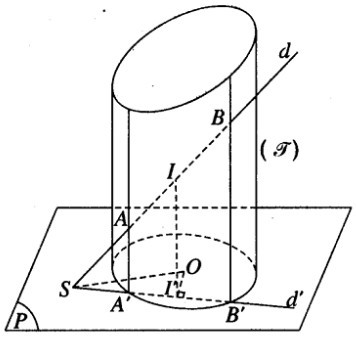
Gọi (P) là mặt phẳng đi qua S và vuông góc với trục của mặt trụ \((\Im )\)
Mặt phẳng (P) cắt \((\Im )\) theo một đường tròn tâm O.
Ta xét một vị trí của đường thẳng d.
Gọi A, B là giao điểm của d với \((\Im )\) và I là trung điểm của đoạn AB.
Chiếu A, B, I theo phương vuông góc với mặt phẳng (P) ta được các điểm theo thứ tự là A’ , B’ , I’ thẳng hàng với S, trong đó A’, B’ nằm trên đường tròn tâm O trong mặt phẳng (P) và I’ là trung điểm của đoạn A’B’.
Do đó điểm I’ luôn luôn nằm trên đường tròn đường kính SO trong mặt phẳng (P) và đường thẳng II’ vuông góc với (P).
Ta suy ra đường thẳng II’ nằm trên mặt trụ \((\Im )\) chứa đường tròn đường kính SO nằm trong (P) và có trục song song với trục của mặt trụ \((\Im )\)
Tất nhiên, điểm I chỉ nằm trong phần mặt trụ \((\Im )\) thuộc miền trong của mặt trụ \((\Im )\)
9. Giải bài 2.9 trang 47 SBT Hình học 12
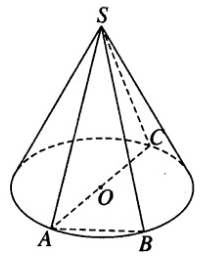
Một khối trụ có bán kính đáy bằng r và chiều cao bằng \(r\sqrt 3\)
Gọi A và B là hai điểm trên hai đường tròn đáy sao cho góc được tạo thành giữa đường thẳng AB và trục của khối trụ bằng 300.
a) Tính diện tích của thiết diện qua AB và song song với trục của khối trụ.
b) Tính góc giữa hai bán kính đáy qua A và B.
c) Xác định và tính độ dài đoạn vuông góc chung của AB và trục của khối trụ.
Phương pháp giải
a) Xác định thiết diện và tính diện tích.
b) Xác định góc giữa hai bán kính và tính toán dựa vào các kiến thức hình học đã biết.
c) Xác định đoạn vuông góc chung của AB và trục khối trụ, từ đó tính độ dài.
Hướng dẫn giải
a) Từ A và B dựng các đường sinh AA’ và BB’ ta có thiết diện qua AB và song song với trục là hình chữ nhật AA’BB’.
Vì OO'//BB' nên góc giữa AB và OO' là góc giữa AB và BB' hay \(\displaystyle \widehat {ABB'}\).
Do đó, \(\displaystyle \widehat {ABB'} = {30^0}\)
Vậy \(\displaystyle AB' = BB'\tan {30^0} = r\sqrt 3 .{1 \over {\sqrt 3 }} = r\)
Do đó diện tích tứ giác AA’BB’ là \(\displaystyle {S_{{\rm{AA}}'BB'}} = AB'.BB' = r.r\sqrt 3 = {r^2}\sqrt 3\)
b) Bán kính đáy qua A là OA; bán kính đáy qua B là O'B.
Vì O'B//OB' nên góc giữa OA và O’B là góc giữa OA và OB' hay \(\displaystyle \widehat {AOB'}\)
Vì AB’ = r nên AOB’ là tam giác đều, do đó \(\displaystyle \widehat {AOB}' = {60^0}\)
c) Mặt phẳng (ABB’) chứa AB và song song với trục OO’ của hình trụ.
Gọi H là trung điểm của AB’. Ta có \(\displaystyle OH \bot (ABB')\)
Đường thẳng qua H song song với OO’ cắt AB tại I.
Dựng IK // HO cắt OO’ tại K.
Ta có: \(OH \bot OO' \Rightarrow IK \bot OO'\)
Lại có \(OH \bot \left( {ABB'} \right) \Rightarrow IK \bot \left( {ABB'} \right) \Rightarrow IK \bot AB\)
Do đó IK là đoạn vuông góc chung của AB và OO'.
Mà \(\displaystyle IK = HO = {{r\sqrt 3 } \over 2}\) nên \(d\left( {AB,OO'} \right) = \frac{{r\sqrt 3 }}{2}\)
10. Giải bài 2.10 trang 48 SBT Hình học 12
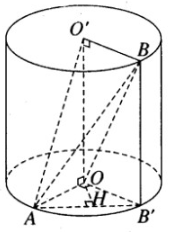
Một hình trụ có các đáy là hai hình tròn tâm O và O’ bán kính r và có đường cao \(h = r\sqrt 2\). Gọi A là một điểm trên đường tròn tâm O và B là một điểm trên đường tròn tâm O’ sao cho OA vuông góc với O’B.
a) Chứng minh rằng các mặt bên của tứ diện OABO’ là những tam giác vuông. Tính thể tích của tứ diện này.
b) Gọi \((\alpha )\) là mặt phẳng qua AB và song song với OO’. Tính khoảng cách giữa trục OO’ và mặt phẳng \((\alpha )\)
c) Chứng minh rằng \((\alpha )\) tiếp xúc với mặt trụ trục OO’ có bán kính bằng \({{r\sqrt 2 } \over 2}\) dọc theo một đường sinh.
Phương pháp giải
a) Sử dụng các kiến thức đã học để kiểm tra các tam giác mặt bên của tứ diện là hình tam gíac vuông.
Tính thể tích theo công thức \(V = \dfrac{1}{3}Sh\)
b) Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng và hình chiếu của đường thẳng lên mặt phẳng đó.
c) Chỉ ra mặt trụ và kết luận.
Hướng dẫn giải
a) Vì trục OO’ vuông góc với các đáy nên \(\displaystyle {\rm{OO}}' \bot OA;{\rm{O}}O' \bot O'B\)
Vậy các tam giác AOO’ và BO’O vuông tại O và O’.
Theo giả thiết ta có \(\displaystyle AO \bot O'B\) mà \(\displaystyle AO \bot {\rm{OO}}' = > AO \bot ({\rm{OO}}'B)\)
Do đó, \(\displaystyle AO \bot OB\) nên tam giác AOB vuông tại O.
Tương tự, ta chứng minh được tam giác AO’B vuông tại O’. Thể tích hình chóp OABO’ là: \(\displaystyle V = {1 \over 3}{S_{\Delta {\rm{OO}}'B}}.AO\)
Hay \(\displaystyle V = {1 \over 3}.{1 \over 2}OO'.O'B.AO \displaystyle = {1 \over 6}.r\sqrt 2 .{r^2} = {{\sqrt 2 } \over 6}{r^3}\)
b) Ta có \(\displaystyle (\alpha )\) là (ABB’).
Vì OO’ // \(\displaystyle (\alpha )\) nên khoảng cách giữa OO’ và \(\displaystyle (\alpha )\) bằng khoảng cách từ O đến \(\displaystyle (\alpha )\)
Dựng \(\displaystyle OH \bot AB'\) ta có \(\displaystyle OH \bot (\alpha )\)
Tam giác OAB' vuông cân tại O có OA=OB'=r nên \(AB' = \sqrt {O{A^2} + OB{'^2}} = \sqrt {{r^2} + {r^2}} = r\sqrt 2\)
\(OH \bot AB'\) nên OH cũng là đường trung tuyến của tam giác \(\Rightarrow OH = \frac{1}{2}AB' = \frac{{r\sqrt 2 }}{2}\)
Vậy khoảng cách cần tìm là \(\displaystyle OH = {{r\sqrt 2 } \over 2}\)
c) Đường tròn tâm O có bán kính bằng \(\displaystyle {{r\sqrt 2 } \over 2}\) tiếp xúc với AB’ tại H là trung điểm của AB’.
Do đó mặt phẳng \(\displaystyle (\alpha )\) song song với trục OO’ chứa tiếp tuyến của đường tròn đáy, nên \(\displaystyle (\alpha )\) tiếp xúc với mặt trụ dọc theo một đường sinh, với mặt trụ có trục OO’ và có bán kính đáy bằng \(\displaystyle {{r\sqrt 2 } \over 2}\)
11. Giải bài 2.11 trang 48 SBT Hình học 12
Một hình trụ có bán kính đáy bằng 50 cm và có chiều cao h = 50 cm.
a) Tính diện tích xung quanh của hình trụ và thể tích của khối trụ được tạo nên.
b) Một đoạn thẳng có chiều dài 100 cm và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách từ đoạn thẳng đó đến trục hình trụ.
Phương pháp giải
a) Diện tích xung quanh \({S_{xq}} = 2\pi Rh\)
b) Xác định đoạn vuông góc chung của đoạn thẳng đó với trục hình trụ và tính toán.
Hướng dẫn giải
a) Ta có công thức \({S_{xq}} = 2\pi rl\) với r = 50 cm, l = 50 cm.
Do đó \({S_{xq}} = 2\pi .50.50 = \pi .5000(c{m^2})\) và \(V = \pi {r^2}h = 125000.\pi (c{m^3})\)
b) Giả sử đoạn thẳng AB có điểm mút A nằm trên đường tròn đáy tâm O’ .
Theo giả thiết ta có: AB = 100 cm. Giả sử IK là đoạn vuông góc chung của trục OO’ và đoạn AB với I thuộc OO’ và K thuộc AB.
Chiếu vuông góc đoạn AB xuống mặt phẳng đáy chứa đường tròn tâm O’ , ta có A’ , H , B lần lượt là hình chiếu của A, K, B.
Vì \(KI \bot OO'\) nên IK // mp(O’BA’) , do đó O’H // IK và O’H = IK.
Ta suy ra \(O'H \bot AB\) và \(O'H \bot AA'\). Vậy \(O'H \bot A'B\)
Xét tam giác vuông AA’B ta có \(A'B = \sqrt {A{B^2} - AA{'^2}} = \sqrt {{{100}^2} - {{50}^2}} = 50\sqrt 3\)
Vậy \(IK = O'H = \sqrt {O'{A^2} - A'{H^2}}\)
\(= \sqrt {{{50}^2} - {{({{50\sqrt 3 } \over 2})}^2}} = 50\sqrt {1 - {3 \over 4}} = 25(cm)\)
12. Giải bài 2.12 trang 48 SBT Hình học 12
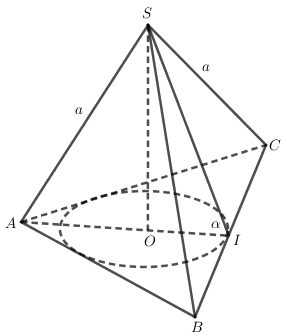
Hình chóp tam giác đều S.ABC có SA = SB = SC = a và có góc giữa mặt bên và mặt phẳng đáy bằng \(\alpha \). Tính diện tích xung quanh của hình trụ có đường tròn đáy là đường tròn nội tiếp tam giác đáy của hình chóp và có chiều cao bằng chiều cao của hình chóp. Các mặt bên SAB , SBC , SCA cắt hình trụ theo những giao tuyến như thế nào?
Phương pháp giải
Sử dụng công thức tính diện tích xung quanh: \({S_{xq}} = 2\pi Rh\)
Hướng dẫn giải
Theo giả thiết ta có tam giác đáy ABC là tam giác đều.
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = a. Đặt OI = r , SO = h , ta có AO = 2r và \(\displaystyle \widehat {SIA} = \alpha\)
Do đó \(\displaystyle \left\{ {\matrix{{h = r\tan \alpha } \cr {{a^2} = {h^2} + 4{r^2}} \cr} } \right.\)
Vậy \(\displaystyle {a^2} = {r^2}{\tan ^2}\alpha + 4{r^2} = {r^2}({\tan ^2}\alpha + 4)\)
Ta suy ra \(\displaystyle r = {a \over {\sqrt {{{\tan }^2}\alpha + 4} }} \,\, và \,\,\displaystyle h = {{a.\tan \alpha } \over {\sqrt {{{\tan }^2}\alpha + 4} }}\)
Gọi Sxq là diện tích xung quanh của hình trụ ta có công thức \(\displaystyle {S_{xq}} = 2\pi rl\) trong đó \(\displaystyle r = {a \over {\sqrt {{{\tan }^2}\alpha + 4} }}\) và \(\displaystyle l = h = {{a\tan \alpha } \over {\sqrt {{{\tan }^2}\alpha + 4} }}\)
Vậy \(\displaystyle {S_{xq}} = 2\pi .{{{a^2}\tan \alpha } \over {{{\tan }^2}\alpha + 4}}\)
Các mặt bên SAB, SBC, SCA là những phần của ba mặt phẳng không song song với trục và cũng không vuông góc với trục nên chúng cắt mặt phẳng xung quanh của hình trụ theo những cung elip. Các cung này có hình chiếu vuông góc trên mặt phẳng (ABC) tạo nên đường tròn đáy của hình trụ.
Các em hãy luyện tập bài trắc nghiệm Khái niệm về mặt tròn xoay Toán 12 sau để nắm rõ thêm kiến thức bài học.
Tham khảo thêm
- doc Giải bài tập SBT Toán 12 Bài 2: Mặt cầu