Giải bài tập SGK Vật lý 9 Bài 51: Bài tập quang hình học

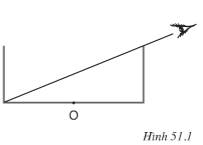
Một bình hình trụ tròn có chiều cao 8cm và đường kính 20 cm. Một học sinh đặt mắt nhìn vào trong bình sao cho thành bình vừa vặn che khuất hết đáy. Khi đổ nước vào khoảng xấp xỉ 2/4 bình thì bạn đó vừa văn nhìn thấy tâm O của đáy. Hãy vẽ tia sáng từ tâm O của đáy bình truyền tới mắt.

Phương pháp giải

- Vẽ mặt cắt dọc của bình theo đúng tỉ lệ. Sau đó vẽ tia sáng từ mép của đáy bình đến mắt.

- Vẽ đường thẳng biểu diễn mặt nước sau khi đổ nước vào bình. Xác định vị trí của điểm tới trên mặt nước. Cuối cùng, vẽ tia sáng truyền từ tâm O của đáy bình đến mặt nước, và từ mặt nước đến mắt.

Hướng dẫn giải

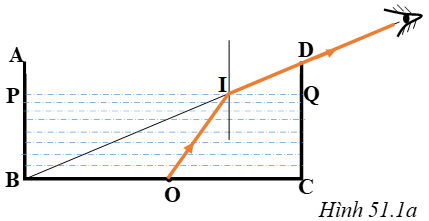
- Vẽ đường thẳng PQ biểu diễn mặt nước sau khi đổ nước vào đường PQ này cắt tia sáng BD đi từ mép của đáy bình đến mắt tại điểm I.

Vậy I là điểm tới.

- Nối OI: OI là tia tới, tia OI bị khúc xạ tại I theo phương IM.

- IM: tia khúc xạ đến mắt.

⇒ Kết quả đo: AB =0,5cm; A’B’ = 1,5cm

⇒ A’B’ = 3AB

Một vật sáng AB có dạng mũi tên được đặt vuông góc với trục chính của một thấu kính hội tụ, cách thấu kính 16 cm, A nằm trên trục chính. Thấu kính có tiêu cự 12 cm.

a. Hãy vẽ ảnh của vât AB theo đúng tỉ lệ.

b. Hãy đo chiều cao của ảnh và của vật trên hình vẽ và tính xem ánh cao gấp bao nhiêu lần vật.

Phương pháp giải

- Vẽ 2 tia cơ bản, khoảng cách giữa giao điểm của hai tia ló đến trục là độ dài của vật

- Xét các tam giác đồng dạng:

\(\begin{array}{l} {\rm{\Delta }}OAB \sim {\rm{\Delta }}OA'B'\\ \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{OA}}{{OA'}}\end{array}\)

\(\begin{array}{l} {\rm{\Delta OIF}} \sim {\rm{\Delta }}A'B'F'\\ \Rightarrow \frac{{OI}}{{A'B'}} = \frac{{OF'}}{{A'F'}} \end{array}\)

tìm được A'B' = 3 AB

Hướng dẫn giải

a. Vẽ ảnh theo đúng tỷ lệ

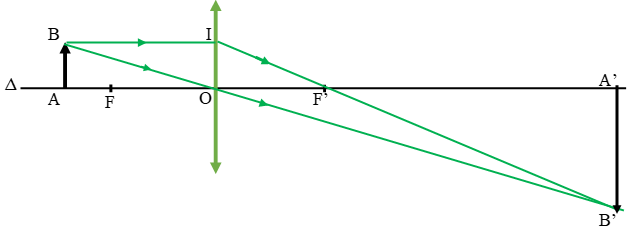
b. Với hình vẽ trên ta đo được AB = 10mm; A'B' = 30mm

=> A'B' = 3AB.

- Dựa vào hình để tính xem chiều cao của vật gấp mấy lần chiều cao của ảnh

OA = 16cm; OF = OF' = 12cm.

Ta có:

\(\begin{array}{l} {\rm{\Delta }}OAB \sim {\rm{\Delta }}OA'B'\\ \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{OA}}{{OA'}}(1) \end{array}\)

Lại có:

\(\begin{array}{l} {\rm{\Delta OIF}} \sim {\rm{\Delta }}A'B'F'\\ \Rightarrow \frac{{OI}}{{A'B'}} = \frac{{OF'}}{{A'F'}}(2) \end{array}\)

Mà: OI = AB (3)

Từ (1), (2) và (3) suy ra: 

\(\begin{array}{l} \frac{{OA}}{{OA'}} = \frac{{{\rm{O}}{{\rm{F}}^\prime }}}{{A'F'}}\\ \Leftrightarrow \frac{{OA}}{{OA'}} = \frac{{{\rm{O}}{{\rm{F}}^\prime }}}{{OA' - O'F'}}\\ \Leftrightarrow \frac{{16}}{{OA'}} = \frac{{12}}{{OA' - 12}} \end{array}\)

⇒OA′=48cm

Thay vào (1) ta có:

\(\begin{array}{l} \frac{{AB}}{{A'B'}} = \frac{{OA}}{{OA'}} = \frac{{16}}{{48}} = \frac{1}{3}\\ \Rightarrow A'B' = 3AB \end{array}\)

Vậy ảnh cao gấp 3 lần vật.

Hòa bị cận thị có điểm cực viễn C_v nằm cách mắt 40 cm. Bình cũng bị cận thị có điểm cực viễn C_v nằm cách mắt 60 cm.

a. Ai bị cận thị nặng hơn?

b. Hòa và bình đều phải đeo kính để khắc phục tật cận thị. Kính được đeo sát mắt. Đó là thấu kính loại gì? Kính của ai có tiêu cự ngắn hơn?

Phương pháp giải

- Mắt cận nhìn rõ những vật ở gần, nhưng không nhìn rõ những vật ở xa. 

- Kính cận là thấu kính phân kì, đeo kính để có thể nhìn rõ những vật ở xa mắt

- Kính cận thích hợp có tiêu điểm F trùng với điểm cực viễn C_v của mắt.

Hướng dẫn giải

a. Ta có: C_v1 = 40cm (Hòa); C_v2 = 60cm (Bình)

Do C_v1 < C_v2 => Hòa bị cận thị nặng hơn.

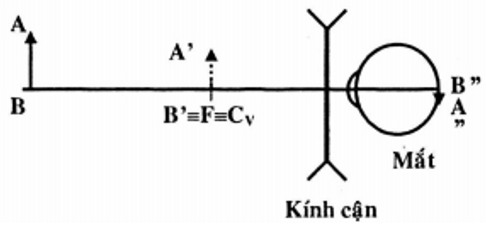
b. Đó là các thấu kính phân kì. Muốn nhìn rõ các vật ở xa thì người cận phải đeo kính có tiêu cự thỏa mãn điều kiện tiêu điểm F của kính trùng với điểm cực viễn của mắt: F ≡ C_v 

Do kính cận thích hợp có tiêu cự f = C_v nên Hoà đeo kính có tiêu cự f₁ = 40cm, Bình đeo kính có tiêu cự f₂ = 60cm. Vậy kính của Hòa có tiêu cự ngắn hơn.