Bài 4: Các thao tác logic hình thức và hình thức logic với khái niệm

Sau khi thu hẹp khái niệm ta thu được khái niệm mới là khái niệm loài của khái niệm giống ban đầu.

Ví dụ: từ khái niệm “nhà thơ”, ta thư hẹp thành khái niệm “nhà thơ Việt Nam”.

Trong thực tiễn, con người có nhu cầu nhận thức sâu sắc hơn về một đối tượng, tìm hiểu chính xác, tỉ mỉ về đối tượng. Quá trình đó chính lầ quá trình thu hẹp khái niệm. Thao tác lôgíc thu hẹp khái niệm là thao tác tư duy hướng vào làm sầu sắc thêm nội hàm khái niệm, trên cơ sở đó thu hẹp ngoại diên của khái niệm ban đầu.

Tuy vậy, việc thu hẹp cũng có giới hạn của nó. Đó  chính là thu hụp đến giới hạn khái niệm cơ sở, mà ố khái' niệm này ngoại diên của nó chỉ còn một đối tưựng duy nhất.

Ví dụ: từ khái niệm .“nhà thờ Việt Nam“. La chi có thể thu họp đốn “nhà thờ cách mạng và là Chủ tịch nước đầu tiên của nước Việt Nam dân chủ cộng hoà”. Đên dây ngoại diên chỉ còn một đối tượng duy nhất là “Hồ Chí Minh” (Hình 8).

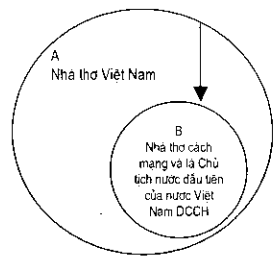
Hình 8

Con người không chỉ có nhu cầu thu hẹp khái niệm mà còn có nhu cầu mỏ rộng khái niệm. Thao tác logic chuyển khái niệm có ngoại diên hẹp với nội hàm phong phú sang khái niệm có ngoại diên rộng với nội hàm nghèo hơn, gọi là mở rộng khái niệm.

Ví dụ: từ khái niệm “nhà thơ” mở rộng thành khái niệm “người lao động trí óc” (Hình 9).

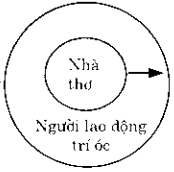
Hình 9

Tuy vậy, thao tác mỏ rộng khái niệm không thể tiếp tục đến vô hạn. Trong khoa học, phạm, trù là khái niệm rộng lớn nhất, vì vậy, khái niệm chỉ có thể mở rộng đến phạm trù. Ví dụ: khái niệm “vật thể” mở rộng đến phạm trù “vật chất”.

Trong hoạt động thực tiễn cũng như trong nhận thức, con người có nhu cầu hiểu rõ bản chất của sự vật và phân biệt nó với các sự vật khác. Đó là công việc căn bản của định nghĩa. Thao tác định nghĩa, chính vì vậy, là quá trình tư duy đi từ cái đã biết đến cái chưa biết, làm cho khái niệm xác định, nghĩa là nó có nội hàm đầy đủ, rõ ràng, không mâu thuẫn, ngoại diên của nó có thể xác định rành mạch. Như vậy, định nghĩa phải đạt được hai yêu cầu; một là, phải phân biệt được sự vật, hiện tượng cần định nghĩa với sự vật, hiện tượng khác, trên phương diện nội dung của nó; hai là, phải làm sáng tỏ nội dung của sự vật, hiện tượng cần định nghĩa.

Tóm lại, định nghĩa khái niệm là thao tác lôgic, nhò đó phát hiện chính xác nội hàm của khái niệm hoặc xác lập ý nghĩa của từ ngữ.

Ví dụ: “hình bình hành” là một tứ giác có các cạnh đôi song song. Trong định nghĩa này, hình bình hành được phân biệt với tập hợp các tứ giác phẳng; dấu hiệu căn bản của nó được xác định là “các cặp cạnh đối song song”.

Trong mỗi định nghĩa bao giờ cùng có hai thành phán: khái niệm cân định nghĩa (cái chưa biết), tức là khái niệm cần phát hiện nội hàm; và khái niệm dừng đê định nghĩa (khái niệm đã biết), nhờ nó phát hiện nội hàm của khái niệm được định nghĩa.

Định nghĩa khái niệm được chia thành định nghĩa duy danh và định nghĩa thực.

Định nghĩa duy danh: Định nghĩa duy danh là định nghĩa xác định thuật ngữ biểu thị đối tượng tư tương.

Ví dụ: “đây là a xít”, “hình này (A) là hình tam giác”.

Định nghĩa duy danh bắt buộc đối tượng phải có mặt khi định nghĩa. Định nghĩa duy danh thực chất mỗi chỉ là định nghĩa từ ngữ biểu đạt khái niệm

Định nghĩa thực: Là định nghĩa làm sáng tỏ nội hàm khái niệm cần được định nghĩa trên cơ sở chỉ rõ những dấu hiệu bản chất của đối tượng cần phải khái quát trong khái niệm.

Ví dụ: “Hình vuông là hình chữ nhật có các cạnh bằng nhau”.

Định nghĩa thực không cần sự có mặt của đối tượng khi định nghĩa.

Định nghĩa thực có nhiều dạng khác nhau. Sau đây chúng ta sẽ nghiên cứu một số dạng cơ bản.

Định nghĩa theo tập hợp

Định nghĩa theo tập hợp thực hiện thông qua việc quy đối tương vào ngoại diên khái niệm giống gần nhất và vạch ra các dấu hiệu dặc trưng, bản chất khác biệt cửa đối tượng, nhằm phân biệt đối tượng cần định nghĩa vối các đối tượng còn lại của khái niệm giống đó. Như vậy, điều kiện để thực hiện định nghĩa tập hợp là phải tồn tại khái niệm giống của khái niệm cần định nghĩa.

Ví dụ: Hình vuông là hình chữ nhật có hai cạnh liên tiếp bằng nhau.

Ở đây, khái niệm giống gần nhất là "hình chữ nhật". Ta vạch ra dấu hiệu bản chất khác biệt của hình vuông là “có hai cạnh liên tiếp bằng nhau”, cái mà các hình chữ nhật khác trong tập hợp hình chữ nhật không có.

Cấu trúc lôgic hình thức của định nghĩa theo tập hợp là: khái niệm A (khái niệm loài) là khái niệm B (khái niệm giông gần nhất) có tính chất C (dấu hiệu bản chất khác biệt của A).

Cần lưu ý rằng, khi khái niệm cần định nghĩa là phạm trù thì không thể định nghĩa theo tập hợp được, vì không tồn tại khái niệm nào bao hàm phạm trù đó.

Định nghĩa theo nguồn gốc

Định nghĩa theo nguồn gốc là định nghĩa vạch ra nguồn gốc tạo thành đối tượng, được định nghĩa trên cơ sở làm phát sinh khái niệm mới đã biết.

Ví dụ: Đường tròn (A) là đường cong khép kín (B) được vạch ra bởi một điểm chuyển động trong một mặt phẳng luôn cách đều một điểm cố định.

Định nghĩa theo nguồn gốc thường được sử dụng trong vật lý, hình học, hoá học, ít sử dụng trong khoa học xã hội.

Định nghĩa theo quan hệ

Định nghĩa theo quan hệ là định nghĩa khái niệm được thực hiện thống qua việc vạch ra quan hệ của khái niệm đó với khái niệm khác.

Cấu trúc lôgic hình thức của định nghĩa là: Khái niệm A là khái niệm có quan hệ R với khái niệm B (R có thê là quan hệ đối lập mâu thuẫn, cũng có thể là quan hộ tương tự, tương đồng hay gần gũi).

Ví dụ:

“Vợ là một người đàn bà có quan hệ hôn nhân với một người đàn ông”.

“Giám đốc công ty là người quyết định điểu hành và quản lý của công ty”.

Định nghĩa hằng miêu tả

Định nghĩa bằng miêu tả là định nghĩa khái niệm thống qua việc liệt kê các dấu hiệu khác biệt bẽn ngoài của đối tượng nhằm phân biệt đối tượng ấy với các đối tượng khác giống nó. Phương pháp định nghĩa này thường được dùng trong văn học, nghệ thuật.

Ví dụ: Nam Cao miêu tả Hoàng trong “Đôi mắt”: “Anh vẫn bước khệnh khạng, thong thả, bởi vì người khí to béo quá, vừa bưổc vừa bơi, hai cánh tay kềnh kênh ra hai bên, những khôi thịt ở hai bên nách kềnh ra và trông tủn ngủn như ngắn quá”.

Định nghĩa bằng so sánh

Có ba dạng định nghĩa bằng so sánh.

• So sánh tương đồng là phương pháp định nghĩa khái niệm trên cơ sở so sánh các đổi tượng, vạch ra các dấu hiệu tường tự với dâu hiệu cơ bản của đối tượng trong các: đối tượng khác. Ví dụ: mắt sáng như sao,...
• So sánh ngược là phương pháp định nghĩa khái niệm được sử dụng phô biên trong dân ca, ca dao, văn học nghệ thuật và trong giao tiếp. Phương pháp này kêt hợp phương pháp so sánh tương đồng với cách nói ngược nhằm nhấn mạnh nội dung của khái niệm được định nghĩa.

Ví dụ: “Đàn ông nông noi giếng khơi. Đàn bà sâu sắc như cơi đựng trầu”.

• So sánh khác biệt là phương pháp định nghĩa khái niệm bàng so sánh trên cơ sở vạch ra dấu hiệu không tồn tại ở đối tượng cần định nghĩa nhưng lại có trong đổi tượng dùng dể so sánh với nó khi định nghĩa. Ví dụ: “Khí trơ là một loại khí không tham gia vào các phản ứng hoá học”.

Quy tắc 1: Định nghĩa phải cân đối

Định nghĩa phải cấn đối có nghĩa là ngoại diên của khái niệm cần định nghĩa phải trùng với ngoại diên của khái niệm dùng để định nghĩa (A = B). Ví dụ: Tam giác đều (A) là tam giác có ba cạnh bằng nhau (B). A = B

Quy tắc 2: Định nghĩa không được luẩn quẩn

Khi định nghĩa, khái niệm để định nghĩa lại giải thích qua khái niệm được định nghĩa thì gọi là định nghĩa luẩn quẩn.

Ví dụ: Người chăm chỉ là người làm việc nhiều. Người làm việc nhiều là người ít nghỉ ngơi, Người ít nghỉ ngơi là người chăm chỉ (Hình 10).

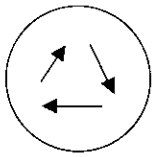
Hình 10

Quy tắc 3: Định nghĩa phải rõ ràng, chính xác, ngắn gọn

Để định nghĩa được rõ ràng, từ ngữ sử dụng phải chuẩn xác, nội dung căn bản của định nghĩa được sắp xếp hợp lý; tóm lại là cách diễn đạt gọn gàng, không rườm rà, đa nghĩa.

Quy tắc 4: Định nghĩa không được phủ định

Ví dụ: “Người vô thần - người không thừa nhận có thần thánh”; “tình yêu không phải là tội lỗi”. Đây không phải là định nghĩa, vì đây không vạch được nội hàm của khái niệm, không thể phát hiện bản chất của đối tượng.

• Nếu như định nghĩa khái niệm làm sáng tỏ nội hàm khái niệm thì phân chia khái niệm vạch rõ ngoại diên của chúng.
• Thực chất của phân chia khái niệm là hướng tư duy phân tích khái niệm giống thành các lớp khái niệm loài.
• Khái niệm giống gọi là khái niệm bị phân chia; còn các khái niệm loài gọi là các khái niệm phân chia hay thành phần phân chia. Dấu hiệu dùng để phân chia khái niệm gọi là cơ sở phân chia hay là căn cứ, tiêu chuẩn phân chia.

Vậy, phản chia khái niệm là thao tác lôgic chia các đối tượng thuộc ngoại diên khái niệm cần phải phân chia thành các nhóm theo những tiẻu chuân nhất định.

Quy tắc phân chia khái niệm

Quy tắc 1: Phán chia phải cân đối

Quy tắc này đòi hỏi tông ngoại diên của các thành phần phân chia phải đúng bằng ngoại diên của khái niệm bị phân chia. Nêu vi phạm nguyên tắc này dẫn đến phân chìa thừa và phân chia thiếu.

•  Phân chia thừa: Ngoại diên khái niệm bị phân chia nhỏ hớn tong ngoại diên các thành phần phân chia. Ví dụ: “Tam giác” được chia thành: “tam giác có 3 góc nhọn”; “tam giác có một góc vuông”; “tam giác có một góc tù”; “tam giác đều” và “tam giác có ba góc bằng nhau”. Ở đây tam giác đều được tính hai lần, do đó tổng ngoại diên của các khái niệm thành phần phân chia lớn hơn ngoại diên khái niệm bị phân chia.
• Phân chia thiếu: Tổng ngoại diên các thành phần phân chia nhỏ hơn ngoại diên khái niệm bị phân chia. Ví dụ: khái niệm “tam giác” phân chia thành hai thành phần: “tam giác vuông” và “tam giác tù”.

Quy tắc 2: Các thành phần phân chia là các khái niệm có quan hệ loại trừ nhau.

Ví dụ: “chiên tranh” phân chia thành “chiến tranh chính nghĩa” và “chiến tranh phi nghĩa”.

Quy tắc 3: Phân chia phải nhất quán theo một tiêu chuẩn xác định.

Ví dụ: Nếu phân chia khái niệm “người” thành “người châu Á”, “người châu Phi”, “người châu Mỹ”, “người tóc vàng”, “người tóc đen", thì sẽ vi phạm nguyên tắc trên.

Quy tắc 4: Phân chia phải hên tục, không được vượt cấp.

Ví dụ: tốc độ vũ trụ gồm có:

• V1 = 7,9 km/s
• V2 - 11,2 km/s
• V3 = 14,6 km/s

Nếu bỏ sót V2 là vượt cấp.

Phân loại khái niệm

Phân loại khái niệm là sự sắp xếp các đối tượng thành từng nhóm sao cho mỗi nhóm giữ một vị trí xác định theo một thứ bậc nhất định. Thực chất đây là phân chia liên tiếp khái niệm giống thành các khái niệm loài nhỏ dần.

Có hai loại phân loại khái niệm:

• Phần loại hổ trự: Đáp ứng các nhu cầu chủ quan tiện lợi cho việc nghiên cứu hay trong thực tiễn sinh hoạt hàng ngày. Ví dụ: Phân loại học sinh trong lớp theo vần chữ cái; phân loại các đơn vị quân đội theo vần chữ cái: F là sư đoàn, E là trung đoàn, D là tiểu đoàn, C là đại đội, B là trung đội, A là tiểu đội.
• Phân loại tự nhiên: Là sự sắp xếp các đối tượng theo lớp xác định dựa trên các dấu hiệu bản chất của chúng. Ví dụ: “sinh vật” phân loại thành “thực vật” và “động sống” và “động vật có xương sống”: “động vật có xương sống” phân loại thành “động vật có vú” và "động vật không có vú”.

Các phần trên đã xem xét những biểu hiện lôgic hình thức của khái niệm. Hình thức của những khái niệm dưới dạng lôgic nghĩa là dưới dạng phổ quát nhất có thể biểu đạt bằng ngôn ngữ lôgic toán học. Ký hiệu tập hợp các đối tượng khái niệm bao quát (ngoại diên của khái niệm) bằng chữ X, tập hợp các dấu hiệu đặc trưng cơ bản của tập hợp X đó (nội hàm của khái niệm) bằng chữ p. Khi đó, hình thức lôgic của khái niệm có thể biểu đạt như sau: xP(x).

Biểu thức xP(x) là ký hiệu tượng trưng của mọi khái niệm, chỉ cần thay thế X và p bằng nội dung cụ thể thì người ta sẽ thu được khái niệm xác định.

Nhằm giúp các bạn sinh viên có thêm tư liệu tham khảo, eLib.VN đã tổng hợp nội dung bài giảng Bài 4: Các thao tác logic hình thức và hình thức logic với khái niệm môn Logic học và chia sẻ đến các bạn trên đây. Hy vọng tư liệu này giúp các bạn nắm bắt nội dung bài học dễ dàng hơn.