Giải bài tập SBT Vật Lí 12 Bài 2: Con lắc lò xo

8. Giải bài 2.8 trang 7 SBT Vật lý 12

9. Giải bài 2.9 trang 7 SBT Vật lý 12

10. Giải bài 2.10 trang 7 SBT Vật lý 12

11. Giải bài 2.11 trang 7 SBT Vật lý 12

12. Giải bài 2.12 trang 7 SBT Vật lý 12

13. Giải bài 2.13 trang 8 SBT Vật lý 12

14. Giải bài 2.14 trang 8 SBT Vật lý 12

Một con lắc lò xo có biên độ A=10,0cm, có tốc độ cực đại 1,2m/s và có cơ năng 1J. Hãy tính:

a) Độ cứng của lò xo.

b) Khối lượng của quả cầu con lắc.

c) Tần số dao động của con lắc.

Phương pháp giải

- Vận dụng công thức tính cơ năng:

\({\rm{W}} = \frac{1}{2}k{A^2} = \frac{1}{2}m{v_{\max }}^2\)

để tìm độ cứng: \({k = \frac{{2W}}{{{A^2}}}}\) và khối lượng là: \({m = \frac{{2W}}{{{v_{{{\max }^2}}}}}}\)

- Sử dụng công thức tính tần số dao động:

\(f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \)

Hướng dẫn giải

Ta có: A=10cm=0,1m

a) Độ cứng của lò xo:

\(\begin{array}{l} {\rm{W}} = {W_{{t_{\max }}}} = \frac{1}{2}k{A^2}\\ \Rightarrow k = \frac{{2W}}{{{A^2}}} = \frac{{2.1}}{{{{0,1}^2}}} = 200(N/m) \end{array}\)

b) Khối lượng là:

\(\begin{array}{l} {\rm{W}} = {{\rm{W}}_{{d_{\max }}}} = \frac{1}{2}mv_{\max }^2\\ \Rightarrow m = \frac{{2W}}{{v_{\max }^2}} = \frac{{2.1}}{{{{1,2}^2}}} = 1,39(kg) \end{array}\)

c) Tần số dao động:

\(f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} = \frac{1}{{2\pi }}\sqrt {\frac{{200}}{{1,39}}} = 1,9(Hz)\)

Một vật có khối lượng 10g dao động điều hòa với biên độ 24cm và chu kì 4,0s. Tại thời điểm t=0, vật ở vị trí biên x=−A.

a) Viết phương trình dao động của vật.

b) Tính li độ, gia tốc và lực kéo về tại thời điểm t=0,5s.

c) Xác định thời điểm đầu tiên vật qua vị trí có li độ x=−12cm và tốc độ của vật tại thời điểm đó.

Phương pháp giải

a) Dựa theo các số liệu bài cho để tìm ω, tìm A, tìm pha ban đầu φ và viết phương trình

b) Thay t vào biểu thức li độ, gia tốc, lực kéo về

- \({x = 24\cos (\frac{\pi }{2}t + \pi )}\)

- \({a = - 12.{{(\frac{\pi }{2})}^2}\cos (\frac{\pi }{2}t + \pi )}\)

- F = m|a|

c) Sử dụng hình tròn lượng giác để tính t

Tốc độ được tính theo công thức:

\(v = \omega \sqrt {{A^2} - {x^2}} \)

Hướng dẫn giải

a) Viết phương trình dao động của vật

- Tần số góc: ω = 2π/T = 2π/4 = π/2 (rad/s)

- Biên độ: A=24cm

- Tìm φ: 

t=0: x₀ = Acosφ = −A

⇔ cosφ =−1 ⇔ φ = π(rad)

- Vậy phương trình dao động:

\(x = 24\cos (\frac{\pi }{2}t + \pi )(cm)\)

b) Phương trình gia tốc: 

\(\begin{array}{l} a = - A{\omega ^2}\cos (\omega t + \varphi )\\ = - 12.{(\frac{\pi }{2})^2}\cos (\frac{\pi }{2}t + \pi )(cm/{s^2}) \end{array}\)

- Tại thời điểm t=0,5s:

- Li độ: 

\(\begin{array}{l} x = 24\cos (\frac{\pi }{2}t + \pi )\\ = 24\cos (\frac{\pi }{2}.0,5 + \pi ) = - 12\sqrt 2 (cm) \end{array}\)

- Gia tốc: 

\(a = - 12.{(\frac{\pi }{2})^2}\cos (\frac{\pi }{2}t + \pi )\)

\(\begin{array}{l} = - 12.{(\frac{\pi }{2})^2}\cos (\frac{\pi }{2}.0,5 + \pi )\\ = 41,9(cm/{s^2}) \end{array}\)

- Lực kéo về: 

F = m|a| = 0,01.0,419 =4,19.10⁻³(N) 

c) Thời điểm đầu tiên vật đi qua li độ x=−12cm là

- Vị trí xuất phát: x=−A

- Vị trí đích: x=−12cm

- Vẽ vòng tròn lượng giác: 

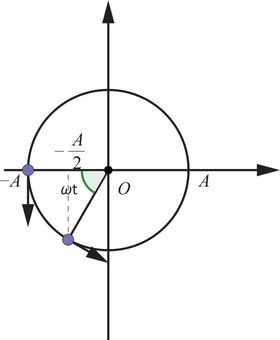
- Từ hình vẽ: cos(ωt) = 1/2

⇒ ωt = π/3 ⇔ π/2t = π/3 ⇔ t = 23s

- Tốc độ tại thời điểm đó: 

\(v = \omega \sqrt {{A^2} - {x^2}} \)

\( = \frac{\pi }{2}\sqrt {{{24}^2} - {{( - 12)}^2}} = 32,6(cm/s)\)

Một con lắc lò xo gồm một vật nhỏ khối lượng 200g gắn với một lò xo nhẹ, dao động điều hòa theo trục Ox nằm ngang với tần số 2,5Hz. Trong khi dao động, chiều dài lò xo biến thiên từ l₁=20cm đến l₂=24cm.

a) Tính biên độ dao động của vật và chiều dài của lò xo khi chưa biến dạng.

b) Viết phương trình dao động của vật, biết khi t=0 vật ở vị trí biên x=+A.

c) Tính vận tốc và gia tốc của vật khi vật đi qua vị trí cân bằng.

Phương pháp giải

a) Độ dài quỹ đạo chuyển động của vật được tính theo công thức

 L = 2A =l₂−l₁

b) Dựa theo các số liệu bài cho để tìm ω, tìm A, tìm pha ban đầu φ và viết phương trình

c) Khi vật qua VTCB, vận tốc và gia tốc được tính bằng công thức:

 v = ±Aω, a = 0

Hướng dẫn giải

a) Độ dài quỹ đạo chuyển động của vật bằng khoảng biến thiên chiều dài của lò xo:

L = 2A = l₂−l₁ = 24−20 = 4cm ⇒ A=2cm

Chiều dài tự nhiên:

l₀= l₁+A = 20+2 = 22cm

b) Viết phương trình dao động của vật

- Tần số góc:

 ω = 2πf = 2π.2,5 =5π (rad/s)

- Biên độ: A=2cm

- Tìm φ: t=₀: x₀ = Acosφ =A

⇔cosφ = 1⇔ φ=0 (rad)

⇔ cos⁡φ =1 ⇔ φ=0(rad)

Vậy phương trình dao động:

 x = 2cos(5πt) (cm)

c) Khi vật đi qua vị trí cân bằng:

- Vật tốc:

 v = ±Aω = ±2.5π = ±10π (cm/s)

- Gia tốc: a = 0

- Vận tốc có thể âm có thể dương, khi đi qua vị trí cân bằng theo chiều dương v=Aω còn khi đi qua vị trí cân bằng theo chiều âm v=−Aω

Một con lắc dao động điều hòa.

a) Tại li độ x bằng một nửa biên độ thì bao nhiêu phần của cơ năng là thế năng? Bao nhiêu phần là động năng?

b) Tại li độ nào (tính theo biên độ) thì động năng bằng thế năng?

Phương pháp giải

Áp dụng các công thức tính sau:

+ Động năng: \({{\rm{W}}_d} = \frac{1}{2}k({A^2} - {x^2})\)

+ Thế năng: \({{\rm{W}}_t} = \frac{1}{2}k{x^2}\)

+ Cơ năng: \({\rm{W}} = \frac{1}{2}k{A^2}\)

cho từng trường hợp ở câu a và b

Hướng dẫn giải

a) Tại x = A/2:

\(\begin{array}{l} \frac{{{{\rm{W}}_t}}}{W} = \frac{{\frac{1}{2}k{x^2}}}{{\frac{1}{2}k{A^2}}} = {\left( {\frac{x}{A}} \right)^2}\\ = {\left( {\frac{1}{2}} \right)^2} = 0,25 = 25{\rm{\% }} \end{array}\)

Vậy li độ x bằng một nửa biên độ thì 25% của cơ năng là thế năng, 75% là động năng

b) Xác định vị trí:

\(\begin{array}{l} {{\rm{W}}_d} = {{\rm{W}}_t}\\ \Leftrightarrow \frac{1}{2}k({A^2} - {x^2}) = \frac{1}{2}k{x^2}\\ \Leftrightarrow x = \pm \frac{{A\sqrt 2 }}{2} \end{array}\)

Một con lắc lò xo gồm một vật có khối lượng 0,5kg gắn vào đầu tự do của một lò xo nhẹ có độ cứng 20N/m. Con lắc dao động theo trục Ox nằm ngang với biên độ dao động là 3cm. Tính:

a) Cơ năng của con lắc và tốc độ cực đại của vật.

b) Động năng và tốc độ cực đại của vật tại vị trí có li độ 2,0cm

Phương pháp giải

- Áp dụng các công thức sau để tính:

+ Động năng: \({{\rm{W}}_d} = \frac{1}{2}k({A^2} - {x^2})\)

+ Cơ năng: \({{\rm{W}}_d} = \frac{1}{2}k{A^2}\)

- Vận tốc được tính theo công thức:

\({{v_{\max }} = \sqrt {\frac{{2W}}{m}} }\)

Hướng dẫn giải

- Cơ năng của con lắc: 

\(\begin{array}{l} {\rm{W}} = \frac{1}{2}k{A^2}\\ = \frac{1}{2}{.20.0,03^2} = {9.10^{ - 3}}J = 9mJ \end{array}\)

- Vận tốc là:

\(\begin{array}{l} {\rm{W}} = \frac{1}{2}mv_{\max }^2\\ \Rightarrow {v_{\max }} = \sqrt {\frac{{2W}}{m}} = \sqrt {\frac{{{{2.9.10}^{ - 3}}}}{{0,5}}} = 0.19m/s \end{array}\)

b) Tại li độ x=2cm

\(\begin{array}{l} {{\rm{W}}_d} = \frac{1}{2}k({A^2} - {x^2})\\ = \frac{1}{2}.20.({0,03^2} - {0,02^2})\\ = {5.10^{ - 3}}J = 5mJ \end{array}\)

Ta có:

\(\begin{array}{l} {{\rm{W}}_d} = \frac{1}{2}m{v^2}\\ \Rightarrow v = \sqrt {\frac{{2{{\rm{W}}_d}}}{m}} \\ = \sqrt {\frac{{{{2.5.10}^{ - 3}}}}{{0,5}}} = 0,14(m/s) \end{array}\)