Giải bài tập SBT Vật Lí 12 Bài 36: Năng lượng liên kết của hạt nhân - Phản ứng hạt nhân

Lực hạt nhân là lực nào sau đây?

A. Lực điện.

B. Lực từ.

C. Lực tương tác giữa các nuclôn.

D. Lực tương tác giữa các thiên hà.

Phương pháp giải

Lực liên kết giữa các nuclon tạo nên lực hạt nhân

Hướng dẫn giải

- Lực hạt nhân là lực liên kết giữa các nuclon

- Chọn C

Độ hụt khối của hạt nhân \({}_Z^AX\) là

A. Δm= Nm_n−Zm_p.

B. Δm= m−Nm_p−Zm_p.

C. Δm= (Nm_n+Zm_p)−m.

D. Δm= Zm_p−Nm_n.

Với N=A−Z;m,m_p,m_n lần lượt là khối lượng hạt nhân, khối lượng prôtôn và khối lượng nơtron.

Phương pháp giải

Áp dụng công thức tính độ hụt khối: 

Δm=(Nm_n+Zm_p)−m.

Hướng dẫn giải

- Độ hụt khối Δm=(Nm_n+Zm_p)−m.

Với N=A−Z;m,m_p,m_n lần lượt là khối lượng hạt nhân, khối lượng prôtôn và khối lượng nơtron.

- Chọn C

Năng lượng liên kết của một hạt nhân

A. có thể dương hoặc âm.

B. càng lớn thì hạt nhân càng bền.

C. càng nhỏ thì hạt nhân càng bền.

D. có thể bằng 0 với các hạt nhân đặc biệt.

Phương pháp giải

Với các hạt nhân đặc biệt, năng lượng liên kết có thể bằng 0

Hướng dẫn giải

- Năng lượng liên kết của hạt nhân có thể bằng 0 với các hạt nhân đặc biệt.

- Chọn D

Đại lượng nào dưới đây đặc trưng cho mức độ bền vững của một hạt nhân?

A. Năng lượng liên kết.

B. Năng lượng liên kết riêng.

C. Số hạt prôtôn.

D. Số hạt nuclôn.

Phương pháp giải

Năng lượng liên kết riêng đặc trưng cho mức độ bền vững của một hạt nhân

Hướng dẫn giải

- Độ bền vững của hạt nhân được đặc trưng bởi năng lượng liên kết riêng, hạt nhân có năng lượng liên kết riêng càng lớn thì càng bền vững

- Chọn B

Chỉ ra phát biểu sai.

Trong một phản ứng hạt nhân có định luật bảo toàn

A. năng lượng toàn phần.

B. điện tích.

C. động năng.

D. số nuclôn.

Phương pháp giải

Để trả lời câu hỏi này cần nắm được các định luật bảo toàn trong phản ứng hạt nhân

Hướng dẫn giải

- Trong một phản ứng hạt nhân có định luật bảo toàn

+ Bảo toàn số nuclon

+ Bảo toàn điện tích

+ Bảo toàn năng lượng toàn phần

+ Bảo toàn động lượng

- Chọn C

Xác định hạt X trong phương trình sau: 

\(_9^{19}F + _1^1H \to _8^{16}O + X.\)

\(\begin{array}{l} A.\,\,_2^3He.\\ B.\,\,_2^4He.\\ C.\,\,_1^2H.\\ D.\,\,_1^3H. \end{array}\)

Phương pháp giải

Sử dụng bảo toàn điện tích và vảo toàn số nuclon trong phản ứng hạt nhân để xác định hạt nhân X

Hướng dẫn giải

- Bảo toàn điện tích: 

9+1=8+Z⇒Z=2

- Bảo toàn số hạt nuclon: 

19+1=16+A⇒A=4

Vậy X là 42He24He

- Chọn B

Đơn vị đo khối lượng nào không sử dụng trong việc khảo sát các phản ứng hạt nhân?

A. kilôgam.                                B. miligam.

C. gam.                                      D. u.

Phương pháp giải

Kilogam là đơn vị không được dùng trong khảo sát phản ứng hạt nhân

Hướng dẫn giải

- Đơn vị đo khối lượng không sử dụng trong việc khảo sát các phản ứng hạt nhân là kilogam

- Chọn A

Hạt nhân A đang đứng yên thì phân rã thành hạt nhân B có khối lượng m_B và hạt C có khối lượng m_α. Tỉ số giữa động năng của hạt nhân B và động năng của hạt α ngay sau phân rã bằng

A. m_B/m_α.                         B. ( m_B/m_α)².

C. (m_α/m_B)².                     D. m_α/m_B

Phương pháp giải

Để xác định tỉ số giữa động năng của hạt nhân B và động năng của hạt α ta sử dụng định luật bảo toàn động lượng

Hướng dẫn giải

- Phương trình phản ứng hạt nhân: 

A → B + V

- Bảo toàn động lượng:

\(\begin{array}{l} \overrightarrow {{p_B}} + \overrightarrow {{p_\alpha }} = \overrightarrow {{p_A}} = \vec 0\\ \begin{array}{*{20}{l}} { \Rightarrow \overrightarrow {{p_B}} = - \overrightarrow {{p_\alpha }} }\\ { \Leftrightarrow {{\left( {\overrightarrow {{p_B}} } \right)}^2} = {{\left( { - \overrightarrow {{p_\alpha }} } \right)}^2}}\\ { \Leftrightarrow 2{m_B}.{{\rm{W}}_{{d_B}}} = 2{m_\alpha }.{{\rm{W}}_{{d_\alpha }}}}\\ { \Rightarrow \frac{{{{\rm{W}}_{{d_B}}}}}{{{{\rm{W}}_{{d_\alpha }}}}} = \frac{{{m_\alpha }}}{{{m_B}}}} \end{array} \end{array}\)

- Chọn D

Giả sử hai hạt nhân X và Y có độ hụt khối bằng nhau; số nuclôn của hạt nhân X lớn hơn số nuclôn của hạt nhân Y, thì

A. năng lượng liên kết riêng của hai hạt nhân bằng nhau.

B. hạt nhân Y bền vững hơn hạt nhân X.

C. năng lượng liên kết riêng của hạt nhân X lớn hơn năng lượng liên kết riêng của hạt nhân Y.

D. hạt nhân X bền vững hơn hạt nhân Y.

Phương pháp giải

- Hạt nhân có năng lượng liên kết riêng càng lớn thì càng bền vững

- Áp dung công thức tính năng lượng liên kết riêng: 

σ=ΔE/A=Δmc²/A

Hướng dẫn giải

- Ta có công thức tính năng lượng liên kết riêng: 

σ= ΔE/A= Δmc²/A

- Vì

+ Δm_X = Δm_Y

+ A_X > A_Y

⇒σ_X < σ_Y

- Nên hạt nhân Y bền vững hơn hạt nhân X.

- Chọn B

Cho ba hạt nhân X,Y và Z có số nuclôn tương ứng là A_X,A_Y và A_Z với A_X=2A_Y=0,5A_Z. Biết năng lượng liên kết riêng của từng hạt nhân tương ứng là ΔE_X,ΔE_Y và ΔE_Z với ΔE_Z<ΔE_X<ΔE_Y. Sắp xếp các hạt nhân này theo thứ tự tính bền vững giảm dần là:

A. Y,X,Z.                        B. Y,Z,X.

C. X,Y,Z.                        D. Z,X,Y.

Phương pháp giải

- Tính năng lượng liên kết riêng bằng công thức: 

σ= ΔE/A= Δmc²/A

- Hạt nhân có năng lượng liên kết riêng càng lớn thì càng bền vững

Hướng dẫn giải

- Công thức tính năng lượng liên kết riêng:

σ= ΔE/A= Δmc²/A

-  Ta có:

+ A_X=2A_Y=0,5A_Z ⇒ A_Z>A_X>A_Y

+ ΔE_Z<ΔE_X<ΔE_Y

- Vậy σ_Z<σ_X<σ_Y nên thứ tự tính bền vững giảm dần là: Y,X,Z

- Chọn A

Bắn một prôtôn vào hạt nhân \({}_3^7Li\) đứng yên. Phản ứng tạo ra hai hạt nhân X giống nhau bay ra với cùng tốc độ và theo phương hợp với phương tới của prôtôn các góc bằng nhau là 60^o. Lấy khối lượng của mỗi hạt nhân, tính theo đơn vị u, bằng số khối của nó. Tỉ số giữa tốc độ của prôtôn và tốc độ của hạt nhân X là

A. 4.                                           B. 12.

C. 2.                                           D. 14.

Phương pháp giải

- Động lượng của hạt nhân chia làm hai thành phần như hình vẽ

- Áp dụng công thức động lượng: p = mv

- Áp dụng định luật bảo toàn động lượng và chiếu lên phương của p_x để tìm tỉ số giữa tốc độ của prôtôn và tốc độ của hạt nhân X

Hướng dẫn giải

Phương trình phản ứng hạt nhân: 

\(_1^1p + _3^7Li \to X + X\)

- Vậy X là \(\begin{array}{l} _2^4He \end{array}\)

- Bảo toàn động lượng:

\(\overrightarrow {{p_p}} = \overrightarrow {2{p_X}} \)

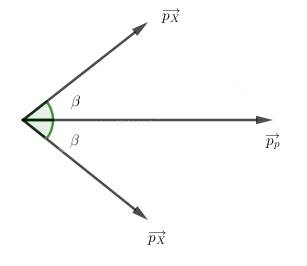
- Chiếu lên phương của \(\vec p_p\)

\(\begin{array}{*{20}{l}} {{p_p} = 2{p_X}\cos \beta }\\ { \Leftrightarrow {m_p}{v_p} = 2{m_X}{v_X}\cos \beta }\\ { \Rightarrow \frac{{{v_p}}}{{{v_X}}} = \frac{{2{m_X}\cos \beta }}{{{m_p}}}}\\ { = \frac{{2.4.\cos {{60}^0}}}{1} = 4} \end{array}\)

- Chọn A

Cho khối lượng của prôtôn, nơ tron; \(_{18}^{40}{\rm{Ar}};_3^6Li\) lần lượt là 1,0073u; 1,0087u; 39,9525u; 6,0145u và 1u=931,5MeV/c². So với năng lượng liên kết riêng của hạt nhân \(_3^6Li\) thì năng lượng liên kết riêng của hạt nhân \(_{18}^{40}{\rm{Ar}}\)

A. lớn hơn một lượng là 5,20MeV.

B. lớn hơn một lượng là 3,42MeV.

C. nhỏ hơn một lượng là 3,42MeV.

D. nhỏ hơn một lượng là 5,20MeV.

Phương pháp giải

- Năng lượng liên kết riêng theo công thức:

 σ=ΔE/A

- Áp dụng công thức tính năng lượng liên kết là:

ΔE=Δmc²

- Áp dụng công thức: 

Δm=Zm_p+(A−Z)m_n−m  để tính độ hụt khối

Hướng dẫn giải

- Năng lượng liên kết của \(_{18}^{40}{\rm{Ar}}\)

\(\begin{array}{*{20}{l}} {{\rm{\Delta }}{E_{{\rm{Ar}}}} = {\rm{\Delta }}m{c^2}}\\ { = (Z{m_p} + (A - Z){m_n} - m){c^2}}\\ { = (18.1,0073 + 22.1,0087 - 39,9525)u{c^2}}\\ { = (18.1,0073 + 22.1,0087 - 39,9525).931,5}\\ { = 344,93445MeV} \end{array}\)

- Năng lượng liên kết riêng của \(_{18}^{40}{\rm{Ar}}\)

\(\begin{array}{l} {\sigma _{{\rm{Ar}}}} = \frac{{{\rm{\Delta }}{E_{{\rm{Ar}}}}}}{{{A_{{\rm{Ar}}}}}} = \frac{{344,93445}}{{40}}\\ = 8,62336125(MeV/nuclon) \end{array}\)

- Năng lượng liên kết của  \(_3^6Li\)

\(\begin{array}{*{20}{l}} {{\rm{\Delta }}{E_{Li}} = {\rm{\Delta }}m{c^2}}\\ { = (Z{m_p} + (A - Z){m_n} - m){c^2}}\\ { = (3.1,0073 + 3.1,0087 - 6,0145)u{c^2}}\\ { = (3.1,0073 + 3.1,0087 - 6,0145).931,5}\\ { = 31,20525MeV} \end{array}\)

- Năng lượng liên kết riêng của \(_3^6Li\)

\(\begin{array}{l} {\sigma _{Li}} = \frac{{{\rm{\Delta }}{E_{Li}}}}{{{A_{Li}}}} = \\ \frac{{31,20525}}{6} = 5,200875(MeV/nuclon) \end{array}\)

So với năng lượng liên kết riêng của hạt nhân \(_3^6Li\) thì năng lượng liên kết riêng của hạt nhân \(_{18}^{40}{\rm{Ar}}\)

lớn hơn một lượng:

\(8,62336125 - 5,200875 \approx 3,42(MeV/nuclon)\)

- Chọn B

Giả sử trong một phản ứng hạt nhân, tổng khối lượng của hai hạt trước phản ứng nhỏ hơn tổng khối lượng của hai hạt sau phản ứng là 0,02u.. Phản ứng hạt nhân này

A. tỏa năng lượng 1,863MeV.

B. tỏa năng lượng 18,63MeV.

C. thu năng lượng 1,863MeV.

D. thu năng lượng 18,63MeV.

Phương pháp giải

Tính nhiệt lượng sau phản ứng theo công thức: 

Q=(m_truoc−m_sau)c²

Hướng dẫn giải

- Ta có:

Q=(m_truoc−m_sau)c²

=−0,02uc²=−0,02.931,5=−18,63MeV<0

⇒ Phản ứng thu năng lượng

- Chọn D

Tính năng lượng liên kết của các hạt nhân \(_5^{11}B\); \(_1^3T\)

Cho biết: m(\(_5^{11}B\))=11,0064u;m(\(_1^3T\))=3,015u.m(511B)

Phương pháp giải

- Áp dụng công thức tính năng lượng liên kết là:

ΔE=Δmc²

- Tính độ hụt khối theo công thức: 

Δm=Zm_p+(A−Z)m_n−m

Hướng dẫn giải

- Năng lượng liên kết của \(_5^{11}B\)

\(\begin{array}{*{20}{l}} {{\rm{\Delta }}{E_B} = {\rm{\Delta }}m{c^2}}\\ { = (Z{m_p} + (A - Z){m_n} - m){c^2}}\\ { = (5.1,0073 + 6.1,0087 - 11,0064)u{c^2}}\\ { = (5.1,0073 + 6.1,0087 - 11,0064).931,5}\\ { = 76,66245MeV} \end{array}\)

- Năng lượng liên kết của \(_1^3T\)

\(\begin{array}{*{20}{l}} {{\rm{\Delta }}{E_T} = {\rm{\Delta }}m{c^2}}\\ { = (Z{m_p} + (A - Z){m_n} - m){c^2}}\\ { = (1.1,0073 + 2.1,0087 - 3,015)u{c^2}}\\ { = (1.1,0073 + 2.1,0087 - 3,015).931,5}\\ { = 9,03555MeV} \end{array}\)

Tính năng lượng liên kết của \(^{234}U\) và \(^{238}U\). Hạt nhân nào bền hơn? Cho biết m(\(^{234}U\))=233,982u; m(\(^{238}U\))=237,997u.

Phương pháp giải

- Năng lượng liên kết: ΔE=Δmc²

- Áp dụng công thức: 

Δm=Zm_p+(A−Z)m_n−m để tính độ hụt khối

- Công thức để tinh năng lượng liên kết riêng là: 

σ=ΔE/A

- Hạt nhân có năng lượng liên kết riêng càng lớn thì càng bền vững

Hướng dẫn giải

- Năng lượng liên kết của \(^{234}U\)

\(\begin{array}{*{20}{l}} {{\rm{\Delta }}{E_1} = {\rm{\Delta }}m{c^2}}\\ { = (Z{m_p} + (A - Z){m_n} - m){c^2}}\\ { = (92.1,0073 + 142.1,0087 - 233,982)u{c^2}}\\ { = (92.1,0073 + 142.1,0087 - 233,982).931,5}\\ { = 1793,1375MeV} \end{array}\)

- Năng lượng liên kết riêng của \(^{234}U\)

\(\begin{array}{l} {\sigma _1} = \frac{{{\rm{\Delta }}{E_1}}}{{{A_1}}}\\ = \frac{{1793,1375}}{{234}} = 7,663(MeV/nuclon) \end{array}\)

- Năng lượng liên kết của \(^{238}U\)

\(\begin{array}{*{20}{l}} {{\rm{\Delta }}{E_2} = {\rm{\Delta }}m{c^2}}\\ { = (Z{m_p} + (A - Z){m_n} - m){c^2}}\\ { = (92.1,0073 + 146.1,0087 - 237,997)u{c^2}}\\ { = (92.1,0073 + 146.1,0087 - 237,997).931,5}\\ { = 1811,5812MeV} \end{array}\)

- Năng lượng liên kết riêng của \(^{238}U\)

\(\begin{array}{l} {\sigma _2} = \frac{{{\rm{\Delta }}{E_2}}}{{{A_2}}}\\ = \frac{{1811,5812}}{{238}} = 7,611(MeV/nuclon) \end{array}\)

σ₁>σ₂ nên \(^{234}U\) bền hơn

Tính năng lượng liên kết riêng của \(_4^9Be;_{29}^{64}Cu;_{47}^{108}Ag.\) Cho biết: m(\(_4^9Be\))=9,0108u; m(\(_{29}^{64}Cu\))=63,913u; m(\(_{47}^{108}Ag\))=107,878u.

Phương pháp giải

Với từng hạt nhân, ta xác định năng lượng liên kết riêng bằng cách sau:

- Công thức tính năng lượng liên kết ΔE=Δmc²

- Trong đó, độ hụt khối được tính bằng công thức: 

Δm=Zm_p+(A−Z)m_n−m

- Áp dụng công thức: σ=ΔE/A để tính năng lượng liên kết riêng

Hướng dẫn giải

- Năng lượng liên kết của \(_4^9Be\)

\(\begin{array}{*{20}{l}} {{\rm{\Delta }}{E_{Be}} = {\rm{\Delta }}m{c^2}}\\ { = (Z{m_p} + (A - Z){m_n} - m){c^2}}\\ { = (4.1,0073 + 5.1,0087 - 9,0108)u{c^2}}\\ { = (4.1,0073 + 5.1,0087 - 9,0108).931,5}\\ { = 57,65985MeV} \end{array}\)

- Năng lượng liên kết riêng của \(_4^9Be\)

\({\sigma _{Be}} = \frac{{{\rm{\Delta }}{E_{Be}}}}{{{A_{Be}}}} = \frac{{57,65985}}{9} = 6,40665(MeV/nuclon)\)

- Năng lượng liên kết của \(_{29}^{64}Cu\)

\(\begin{array}{*{20}{l}} {{\rm{\Delta }}{E_{Cu}} = {\rm{\Delta }}m{c^2}}\\ { = (Z{m_p} + (A - Z){m_n} - m){c^2}}\\ { = (29.1,0073 + 35.1,0087 - 63,913)u{c^2}}\\ { = (29.1,0073 + 35.1,0087 - 63,913).931,5}\\ { = 561,8808MeV} \end{array}\)

- Năng lượng liên kết riêng của \(_{29}^{64}Cu\)

\(\begin{array}{l} {\sigma _{Cu}} = \frac{{{\rm{\Delta }}{E_{Cu}}}}{{{A_{Cu}}}}\\ = \frac{{561,8808}}{{64}} = 8,78(MeV/nuclon) \end{array}\)

- Năng lượng liên kết của \(_{47}^{108}Ag\)

\(\begin{array}{*{20}{l}} {{\rm{\Delta }}{E_{Ag}} = {\rm{\Delta }}m{c^2}}\\ { = (Z{m_p} + (A - Z){m_n} - m){c^2}}\\ { = (47.1,0073 + 61.1,0087 - 107,878)u{c^2}}\\ { = (47.1,0073 + 61.1,0087 - 107,878).931,5}\\ { = 927,5877MeV} \end{array}\)

 - Năng lượng liên kết riêng của \(_{47}^{108}Ag\)

\(\begin{array}{l} {\sigma _{Ag}} = \frac{{{\rm{\Delta }}{E_{Ag}}}}{{{A_{Ag}}}}\\ = \frac{{927,5877}}{{108}} = 8,589(MeV/nuclon) \end{array}\)

Dùng một prôtôn có động năng 5,45MeVbắn vào hạt nhân \(_4^9Be\) đang đứng yên. Phản ứng tạo ra hạt nhân X và hạt α. Hạt αα bay ra theo phương vuông góc với phương tới của prôtôn và có động năng 4MeV. Khi tính động năng của các hạt, lấy khối lượng hạt tính theo đơn vị khối lượng nguyên tử bằng số khối của chúng. Tính năng lượng tỏa ra trong phản ứng này theo đơn vị MeV.

Phương pháp giải

- Áp dụng công thức động lượng: p² = 2m.W

- Sử dụng bảo toàn động lượng trong phản ứng hạt nhân để tìm động năng lúc sau

- Tính năng lượng phản ứng: 

Q=W_dsau−W_dtruoc

Hướng dẫn giải

- Phương trình phản ứng: 

\(_1^1p + _4^9Be \to _3^6X + \alpha \)

- Bảo toàn động lượng:

\(\overrightarrow {{p_p}} = \overrightarrow {{p_X}} + \overrightarrow {{p_\alpha }} \)

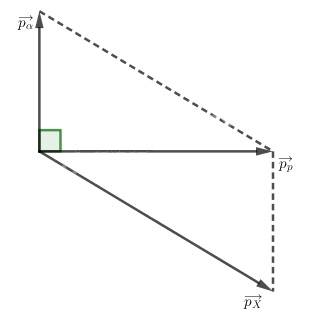
Do \(\vec p_p\) vuông góc với \(\vec p_a\) nên ta có

\(\begin{array}{*{20}{l}} {p_X^2 = p_p^2 + p_\alpha ^2}\\ { \Leftrightarrow 2{m_X}{{\rm{W}}_X} = 2{m_p}{{\rm{W}}_P} + 2{m_\alpha }{{\rm{W}}_\alpha }}\\ { \Rightarrow {{\rm{W}}_X} = \frac{{{m_p}{{\rm{W}}_P} + {m_\alpha }{{\rm{W}}_\alpha }}}{{{m_X}}}}\\ { = \frac{{1.5,45 + 4.4}}{6} = 3,575MeV} \end{array}\)

- Năng lượng phản ứng:

\(\begin{array}{*{20}{l}} {Q = {{\rm{W}}_{{d_{sau}}}} - {{\rm{W}}_{{d_{truoc}}}}}\\ { = {{\rm{W}}_X} + {{\rm{W}}_\alpha } - {{\rm{W}}_p}}\\ { = 3,575 + 4 - 5,45 = 2,125MeV} \end{array}\)

Hạt nhân \(_4^{10}Be\) có khối lượng 10,0135u. Khối lượng của nơtron m_n=1,0087u,khối lượng của prôtôn mp=1,0073u,1u=931Mev/c². Tính năng lượng liên kết và năng lượng liên kết riêng của hạt nhân 

Phương pháp giải

- Tính năng lượng liên kết theo công thức: ΔE=Δmc²

- Độ hụt khối: 

Δm=Zm_p+(A−Z)m_n−m

- Công thức để tính năng lượng liên kết riêng là: σ=ΔE/A

Hướng dẫn giải

- Năng lượng liên kết của \(_4^{10}Be\)

\(\begin{array}{l} \begin{array}{*{20}{l}} {{\rm{\Delta }}{E_{Be}} = {\rm{\Delta }}m{c^2}}\\ { = (Z{m_p} + (A - Z){m_n} - m){c^2}}\\ { = (4.1,0073 + 6.1,0087 - 10,0135)u{c^2}}\\ { = (4.1,0073 + 6.1,0087 - 10,0135).931}\\ { = 63,2149MeV} \end{array}\\ \end{array}\)

- Năng lượng liên kết riêng của \(_4^{10}Be\)

\(\begin{array}{l} {\sigma _{Be}} = \frac{{{\rm{\Delta }}{E_{Be}}}}{{{A_{Be}}}}\\ = \frac{{63,2149}}{{10}} \approx 6,32(MeV/nuclon) \end{array}\)

Bắn một đơteri vào một hạt nhân \(_3^6Li\), ta thu được hai hạt nhân X giống nhau.

a) Viết phương trình phản ứng và cho biết hạt nhân X là hạt nhân gì?

b) Phản ứng này tỏa hay thu năng lượng? Tính năng lượng này.

Cho khối lượng của hạt nhân \(_3^6Li\) là m_Li=6,0145u; của hạt đơteri là m_H=2,0140u; của hạt nhân X là m_X=4,0015u;1u=931MeV/c².

Phương pháp giải

Tính năng lượng phản ứng theo công thức:

Q=(m_truoc−m_sau)c²

Hướng dẫn giải

a) Phương trình phản ứng:

\(_1^2D + _3^6Li \to 2_2^4X\)

b) Năng lương phản ứng:

\(\begin{array}{*{20}{l}} {Q = ({m_{truoc}} - {m_{sau}}){c^2}}\\ { = (2{m_X} - {m_D} - {m_{Li}}){c^2}}\\ { = (2.4,0015 - 2,014 - 6,0145)u{c^2}}\\ { = (2.4,0015 - 2,014 - 6,0145).931}\\ { = 1,3965MeV > 0} \end{array}\)

Phản ứng tỏa năng lượng

Theo thuyết tương đối, một êlectron có động năng bằng một nửa năng lượng nghỉ của nó thì vận tốc của nó sẽ bằng bao nhiêu?

Phương pháp giải

Sử dụng công thức tính động năng:

\({{\rm{W}}_d} = \left[ {\frac{1}{{\sqrt {1 - {{\left( {\frac{v}{c}} \right)}^2}} }} - 1} \right]{E_0} = 0,5{E_0}\)

để tìm vận tốc v

Hướng dẫn giải

Ta có:

\(\begin{array}{l} {{\rm{W}}_d} = \left[ {\frac{1}{{\sqrt {1 - {{\left( {\frac{v}{c}} \right)}^2}} }} - 1} \right]{E_0} = 0,5{E_0}\\ \Rightarrow v = \frac{{\sqrt 5 }}{3}c \end{array}\)