Hướng dẫn cách sử dụng hàm PMT tính số tiền thanh toán hàng kỳ cho khoản vay và cách phân tích trả nợ gốc và lãi cùng chuỗi hàm PMT trong Excel

323 lượt xem
Share

Làm thế nào để sử dụng hàm PMT tính số tiền thanh toán hàng kỳ cho khoản vay và Cách phân tích trả nợ gốc và lãi cùng chuỗi hàm PMT trong Excel một cách nhanh chóng nhất. Hãy đọc bài viết dưới đây do eLib biên soạn để tìm cho mình được câu trả lời chính xác nhất nhé.

Mục lục nội dung

Hướng dẫn cách sử dụng hàm PMT tính số tiền thanh toán hàng kỳ cho khoản vay và cách phân tích trả nợ gốc và lãi cùng chuỗi hàm PMT trong Excel

1. Cách phân tích trả nợ gốc và lãi cùng chuỗi hàm PMT trong Excel

Bạn cần vay một khoản tiền là 100 triệu tại thời điểm hiện tại, trả đều đặn hàng tháng trong vòng 3 năm với lãi suất 6% mỗi tháng. Vậy mỗi tháng phải trả bao nhiêu tiền? Tổng cộng sau 3 năm phải trả cả gốc và lãi là bao nhiêu tiền? Phân tích số tiền gốc, tiền lãi, còn nợ của từng kỳ?

Cách làm:

Để phân tích trả nợ, chúng ta lập 1 bảng xác định rõ từng kỳ thanh toán như sau:

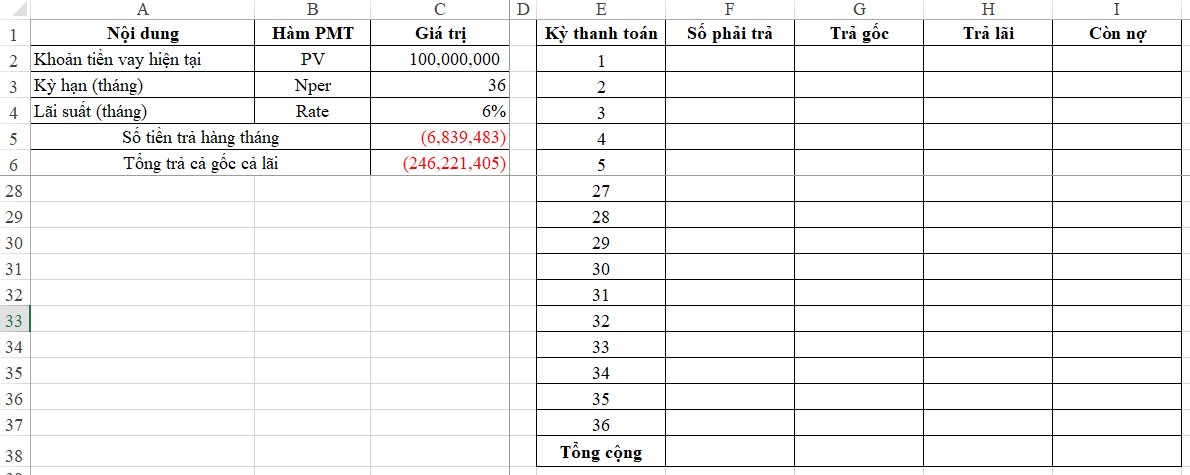
  • Xác định rõ từng kỳ thanh toán
  • Tại mỗi kỳ sẽ xác định các chỉ tiêu: Số phải trả, Số trả gốc, Số trả lãi, số còn nợ

Mỗi chỉ tiêu sẽ được tính cụ thể như sau:

Số phải trả = hàm PMT: F2 =PMT($C$4,$C$3,$C$2)

Các vị trí của tham chiếu trong hàm PMT sẽ cần được cố định để chúng ta có thể tính tiếp cho các kỳ sau.

Trả gốc = hàm PPMT (Principal Part of the Payment)

Cấu trúc hàm PPMT(Rate, Per, Nper, PV, [FV], [Type])

Ở đây xuất hiện thêm 1 tham chiếu là Per = Tại kỳ nào => Xác định cụ thể trả gốc vào kỳ nào. Khoản tiền này sẽ được quy đổi về giá trị tương lai của khoản tiền tại thời điểm kết thúc kỳ hạn trả nợ.

G2 =PPMT($C$4,$E2,$C$3,$C$2)

Trả lãi = hàm IPMT (Interest Part of the Payment)

Cấu trúc hàm IPMT(Rate, Per, Nper, PV, [FV], [Type])

Cấu trúc này tương tự với cấu trúc hàm PPMT, chỉ khác là kết quả của hàm cho chúng ta số tiền là số lãi phải trả, quy đổi về giá trị tương lai của khoản tiền tại thời điểm kết thúc kỳ hạn trả nợ.

H2 =IPMT($C$4,E2,$C$3,$C$2)

Số còn nợ = Khoản vay + Trả gốc (vì trả gốc là số âm)

Số còn nợ = Khoản vay còn lại sau mỗi kỳ – Trả gốc mỗi kỳ

I2 = C2+G2

I3 = I2+G3

I4=I3+G4

…

=> Sau đó Filldown toàn bộ công thức cho các kỳ còn lại để xem kết quả:

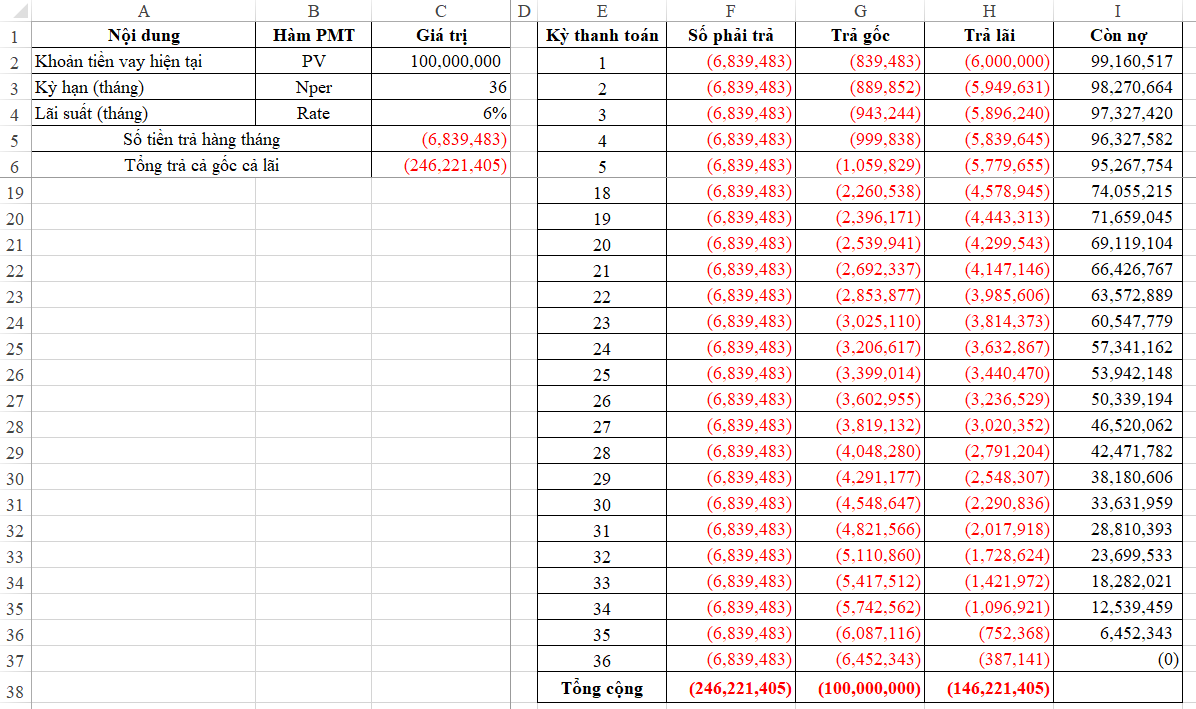
Như vậy chúng ta có thể phân biệt được rõ số gốc và số lãi trong mỗi kỳ thanh toán.

Càng trả nhiều kỳ thì số lãi phải trả càng tăng

Chúng ta thử xét ví dụ trên với số kỳ trả nợ là 12 tháng xem sao:

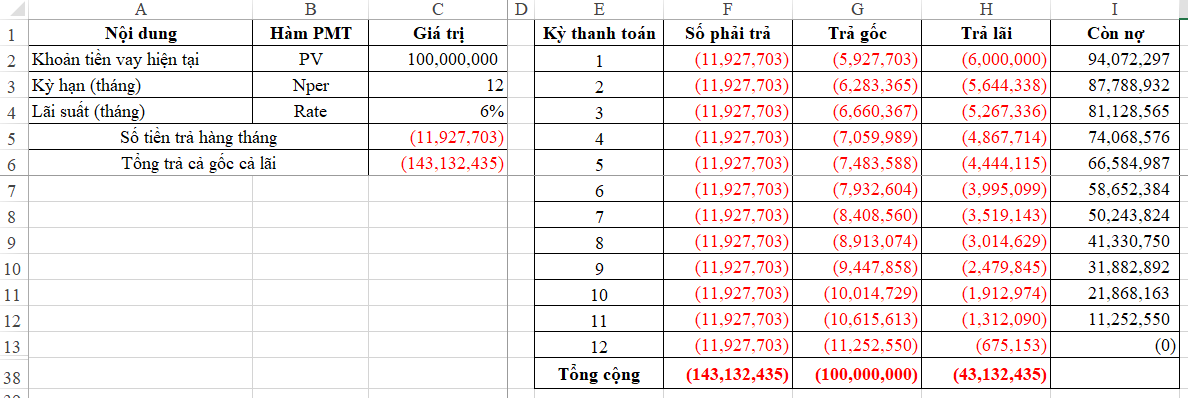
Như vậy chỉ cần giảm số kỳ trả lãi từ 36 xuống 12 thì đã giảm được hơn 100 triệu tiền lãi rồi.

Qua bài học này, chúng ta học thêm được kỹ năng phân tích khoản vay và việc thanh toán khoản vay nhờ vào các hàm PMT trong Excel. Đây là kỹ năng cơ bản nhưng rất quan trọng mà khi làm việc ở mảng tài chính chúng ta đều cần phải nắm được.

2. Cách sử dụng hàm PMT tính số tiền thanh toán hàng kỳ cho khoản vay trong Excel

2.1. Tìm hiểu cấu trúc hàm PMT trong Excel

Cấu trúc hàm PMT như sau: =PMT(rate, nper, pv, [fv], [type])

  • Rate – Bắt buộc – Đây là lãi suất hàng kỳ của khoản vay
  • NPer (total Number of Perior)- Bắt buộc – Đây là tổng số kỳ thanh toán
  • PV (Present Value)- Bắt buộc – Giá trị hiện tại của khoản vay (nợ gốc)
  • FV (Future Value)- Tùy chọn – Giá trị tương lai (hoặc số dư) của khoản tiền sau khi thực hiện việc thanh toán đợt cuối cùng. Nếu không chọn thì hiểu mặc định là sẽ trả hết khoản vay
  • Type – Tùy chọn – chọn giữa số 0 hoặc số 1 – Thời điểm thanh toán là đầu kỳ hay cuối chu kỳ

Lưu ý:

  • RATE và NPER phải thống nhất về cùng 1 giá trị thời gian
  • Nếu NPER bắt buộc tính theo tháng mà đề bài cho lãi suất theo năm thì phải quy đổi RATE về theo tháng

2.2. Ứng dụng hàm PMT vào bài tập

Các chỉ số trong bài tập này được tính như sau:

Rate = 6%/tháng

Nper = 3 năm = 3 * 12 = 36 tháng (quy đổi tương ứng theo Rate, vì yêu cầu tính số tiền trả hàng tháng)

PV = 100 triệu

=> Hàm PMT sử dụng như sau:

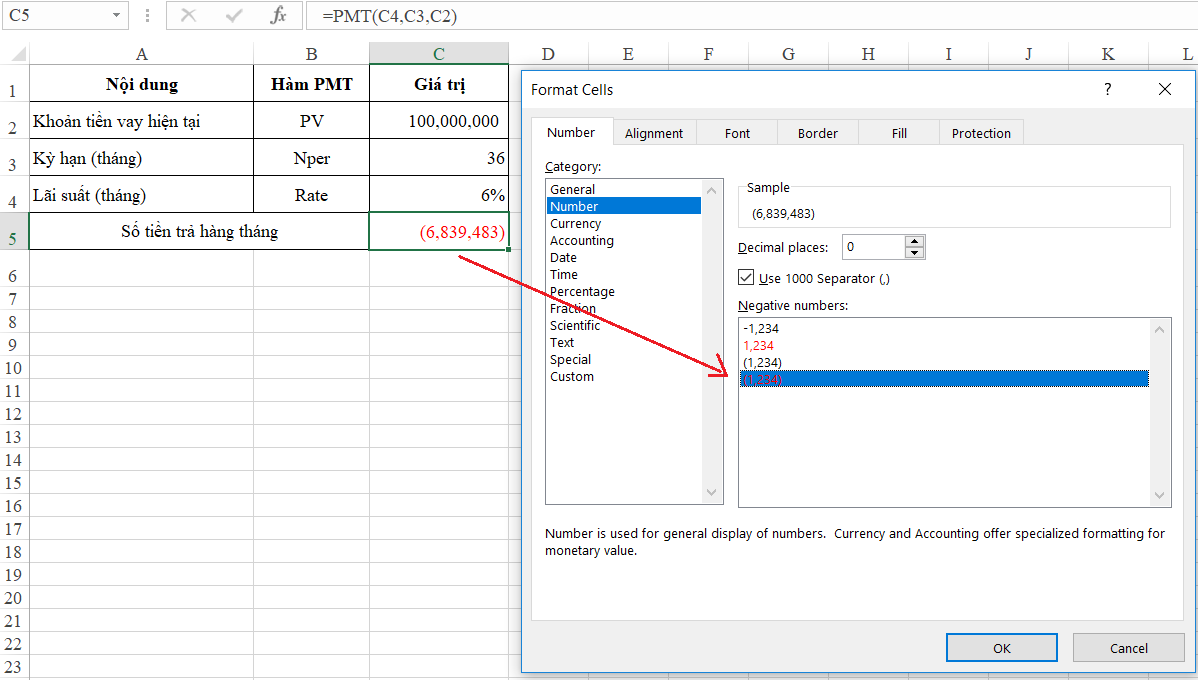
Hàm PMT

 Lưu ý: Kết quả của hàm PMT ra số âm, số tiền ở dạng $ nên có 2 cách để xử lý kết quả hàm PMT:

  • Bỏ dấu $: Format cells ô sử dụng hàm PMT, chọn mục Number (hoặc nếu chọn Currency thì mục Symbol chọn None)
  • Bỏ dấu âm: Giá trị PV sẽ đặt dấu âm thì kết quả của hàm sẽ ra số dương => PMT(Rate, nper, -PV)

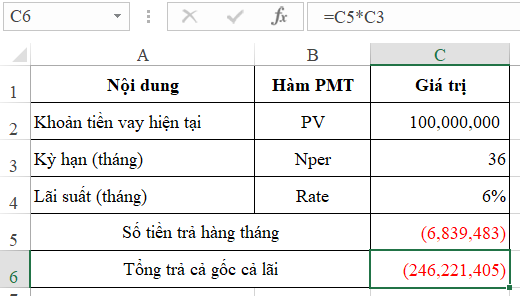
Như vậy mỗi tháng cần trả số tiền là 6.839.483

Số tiền cả gốc cả lãi sau 3 năm là: 6.839.483*36 = 246.221.405

Bảng số liệu

Như vậy là chúng ta đã thực hiện xong yêu cầu của đề bài rồi. Rất đơn giản đúng không nào? Hy vọng rằng bài viết này sẽ giúp ích cho các bạn. Chúc bạn thực hiện thao tác thành công!

 

323 lượt xem
Share
Ngày:14/08/2020 Chia sẻ bởi:
TẢI VỀ XEM ONLINE

CÓ THỂ BẠN QUAN TÂM