Giải bài tập SGK Vật lý 10 Bài 7: Sai số của phép đo các đại lượng Vật lý

Dùng một đồng hồ đo thời gian có độ chia nhỏ nhất 0.001 s để đo n lần thời gian rơi tự do của một vật bắt đầu từ điểm A (v_A = 0) đến điểm B, kết quả cho trong Bảng 7.1.

1. Hãy tính thời gian rơi trung bình, sai số ngẫu nhiên, sai số dụng cụ và sai số phép đo thời gian: Phép đo này trực tiếp hay gián tiếp? Nếu chỉ đo 3 lần (n = 3) thì kết quả đo bằng bao nhiêu?

Bảng 7.1

Phương pháp giải

Để trả lời câu hỏi trên cần thực hiện các bước sau:

• Tính thời gian rơi trung bình \(\overline t \).

• Tính sai số ngẫu nhiên.

• Tính sai số dụng cụ.

• Tính kết quả.

Hướng dẫn giải

- Hoàn thảnh bảng: 

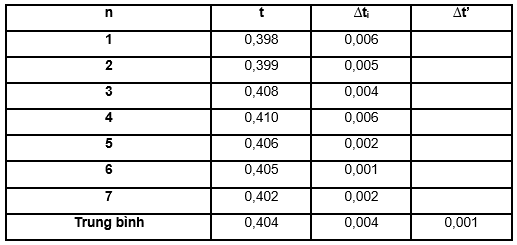
- Ta có:

• Thời gian rơi trung bình \(\overline t \) = 0,404s

• Sai số ngẫu nhiên: ∆t = 0,004 s

• Sai số dụng cụ: ∆t’ = 0,004 + 0,001 = 0,005 s

• Kết quả: t = \(\overline t \) + ∆t  = 0,404 ± 0,005 s

• Đây là phép đo trực tiếp.

• Nếu chỉ đo ba lần: (n = 1, 2, 3) thì kết quả đo phải lấy sai số cực đại.

t = \(\overline t \) ± ∆t

• Với \(\overline t \) = (0,398 + 0,399 + 0,408)/3 ≈ 0,402

 ∆t = 0,006s

\(\small \Rightarrow t = 0,402 \pm 0,006s.\)

Dùng một thước milimet đo 5 lần khoảng cách s giữa hai điểm A,B đều cho một giá trị như nhau bằng 798mm. Tính sai số phép đo này và viết kết quả đo.

Phương pháp giải

Để  tính sai số phép đo này và viết kết quả đo cần đánh giá sai số dụng cụ.

Hướng dẫn giải

• Sai số của phép đo khoảng cách giữa hai điểm AB được đánh giá bởi sai số dụng cụ, lấy ∆S = 1mm

• Kết quả đo được viết: \(\small S = 798 \pm 1mm\).

Cho công thức tính vận tốc tại B:

 \(v =\frac{2s}{t}\) và gia tốc rơi tự do: \(\small g =\frac{2s}{t^{2}}\).

Dựa vào các kết quả đo ở trên và các quy tắc tính sai số đại lượng đo gián tiếp, hãy tính v, g, ∆v, ∆g, δv, δg và viết các kết quả cuối cùng.

Phương pháp giải

Để tính v, g, ∆v, ∆g, δv, δg và viết các kết quả cuối cùng ta cần

• Áp dụng công thức tính sai số tỉ đối δv, δg.
• Áp dụng công thức tính \(\overline v \), \(\overline g \) ⇒ v, g.

Hướng dẫn giải

Áp dụng công thức tính sai số tỉ đối:

\(\delta v = \frac{{\Delta v}}{{\overline v }} = \frac{{\Delta t}}{{\overline t }} = \frac{1}{{798}} + \frac{{0,005}}{{0,404}} = 0,014\)

\(\delta g = \frac{{\Delta g}}{g} = \frac{{\Delta S}}{S} + \frac{{2\Delta t}}{{\overline t }} = \frac{1}{{798}} + 2.\frac{{0,005}}{{0,404}} = 0,026\)

\(\overline v  = \frac{{2\overline S }}{{\overline t }} = 2.\frac{{0,798}}{{0,404}} = 3,95\) m/s

∆v = \(\overline v \).δv = 3,95 . 0,014 = 0,06 m/s

⇒ v = \(\overline v \) ± ∆v = 3,95 ± 0,06 m/s

\(\overline g  = \frac{{2\overline S }}{{\overline {{t^2}} }} = 2.\frac{{0,798}}{{{{0,404}^2}}} = 9,78\) m/s².

∆g = \(\overline g \).δg = 9,78.0,026 = 0,26 m/s².

⇒ g = \(\overline g \) ± ∆g = 9,78 ±  0,26 m/s²