Giải bài tập SBT Vật Lí 10 Bài 14: Lực hướng tâm

Hai vệ tinh nhân tạo I và II bay quanh Trái Đất trên quỹ đạo tròn bán kính lần lượt là r và 2r. Tốc độ của vệ tinh là I và v₁. Hỏi tốc độ v₂ của vệ tinh II là bao nhiêu?

A. 2v₁.                   B. v₁.            

C.  \(\frac{{{v_1}}}{{\sqrt 2 }}\)                    D. v₁/2. 

Phương pháp giải

Vận dụng lí thuyết về độ lớn lực hướng tâm để trả lời câu hỏi này

Hướng dẫn giải

- Tốc độ của vệ tinh II là: \(\frac{{{v_1}}}{{\sqrt 2 }}\)

- Chọn đáp án C

Gia tốc rơi tự do trên bề mặt của Mặt Trăng là g = 1,6 m/s². Bán kính của Mặt Trăng là 1,7.10⁶ m. Chu kì của vệ tinh trên quỹ đạo gần Mặt Trăng gần đúng bằng

A. 1,0.10³ s.      B. 6,5.10³ s.    

C. 5,0.10⁶ s.      D. 7,1.10¹²s. 

Phương pháp giải

Áp dụng công thức:

\(T = \frac{{2\pi }}{\omega } = \frac{{2\pi r}}{v} = \frac{{2\pi r}}{{\sqrt {rg} }}\) để tính chu kì

Hướng dẫn giải

- Chu kì của vệ tinh trên quỹ đạo gần Mặt Trăng là:

\(\begin{array}{l} T = \frac{{2\pi }}{\omega } = \frac{{2\pi r}}{v} = \frac{{2\pi r}}{{\sqrt {rg} }}\\ = 2\pi \sqrt {\frac{r}{g}} = 2\pi \sqrt {\frac{{{{1,7.10}^6}}}{{1,6}}} = {6,5.10^3}s \end{array}\)

- Chọn đáp án B

Một người buộc một hòn đá vào đầu một sợi dây và quay sao cho cả dây và vật chuyển động tròn đều trong mặt phẳng nằm ngang. Muốn hòn đá chuyển động trên đường tròn bán kính 3 m với tốc độ 2 m/s thì người ấy phải giữ dây với một lực bằng 10 N. Khối lượng của hòn đá bằng

A. 22,5 kg.            B. 13,3 kg.        

C. 7,5 kg.              D. 0,13 kg. 

Phương pháp giải

Tính khối lượng theo công thức:

m=F/a với \({a_{ht}} = \frac{{{v^2}}}{r} \)

Hướng dẫn giải

- Gia tốc của hòn đá là:

\({a_{ht}} = \frac{{{v^2}}}{r} = \frac{{{2^2}}}{3} = \frac{4}{3}m/{s^2}\)

- Khối lượng của hòn đá là:

\(\begin{array}{l} F = ma\\ \Rightarrow m = \frac{{10}}{{4/3}} = 7,5kg \end{array}\)

- Chọn đáp án C

Một người buộc một hòn đá vào đầu một sợi dây rồi quay dây trong mặt phẳng thẳng đứng. Hòn đá có khối lượng 0,4 kg, chuyển động trên đường tròn bán kính 0,5 m với tốc độ góc không đổi 8 rad/s. Lấy g = 10 m/s². Hỏi lực căng của dây khi hòn đá ở đỉnh của đường tròn ?

A. 8,8 N.            B. 10,5 N.          

C. 12,8 N.          D. 19,6 N. 

Phương pháp giải

Tính lực căng dây theo công thức:

\({T = m( - g + {\omega ^2}r)}\)

Hướng dẫn giải

- Ta có:

\(\begin{array}{*{20}{l}} {{F_{ht}} = T + mg}\\ { \Rightarrow m{\omega ^2}r = T + mg}\\ { \Rightarrow T = m( - g + {\omega ^2}r)}\\ { = 0,4.( - 10 + {8^2}.0,5) = 8,8N} \end{array}\)

⇒ Lực căng của dây khi hòn đá ở đỉnh của đường tròn là 8,8 N.     

- Chọn đáp án A

Một vệ tinh có khối lượng m = 600 kg đang bay trên quỹ đạo tròn quanh Trái Đất ở độ cao bằng bán kính Trái Đất. Biết Trái Đất có bán kín R = 6 400 km. Lấy g = 9,8 m/s². Hãy tính:

a) tốc độ dài của vệ tinh.

b) chu kì quay của vệ tinh.

c) lực hấp dẫn tác dụng lên vệ tinh. 

Phương pháp giải

a) Tốc độ dài của vệ tinh được tính theo công thức:

\(\begin{array}{l} v = \sqrt {\frac{{GM}}{{2R}}} = \sqrt {\frac{{Rg}}{2}} \end{array}\)

b) Chu kì quay của vệ tinh được tính theo công thức:

\(T = \frac{{4\pi R}}{v} \)

c) Lực hấp dẫn tác dụng tính theo công thức:

\(\begin{array}{l} {F_{ht}} = \frac{{m{v^2}}}{{2R}} \end{array}\)

Hướng dẫn giải

a) Lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm

\(\begin{array}{l} {F_{hd}}\; = {\rm{ }}{F_{ht}}\\ \Rightarrow \frac{{GMm}}{{4{R^2}}} = \frac{{m{v^2}}}{{2R}}\\ = > v = \sqrt {\frac{{GM}}{{2R}}} \end{array}\)

Mặt khác, trên mặt đất ta có:

\(\begin{array}{l} P{\rm{ }} = {\rm{ }}mg = \frac{{GMm}}{{{R^2}}}\\ = > g = \frac{{GM}}{{{R^2}}} = 9,8m/{s^2}\\ \Rightarrow v = \sqrt {\frac{{Rg}}{2}} = \sqrt {\frac{{{{64.10}^5}.9,8}}{2}} \\ = 5600(m/s) = {\rm{ }}5,6{\rm{ }}km/s \end{array}\)

b)  \(T = \frac{{4\pi R}}{v} = \frac{{4.3,{{14.64.10}^5}}}{{5600}} = 14354,29s \approx 240p\)

c. \(\begin{array}{l} {F_{ht}} = \frac{{m{v^2}}}{{2R}} = \frac{{{{600.5600}^2}}}{{2.6400000}} = 1470(N)\\ \Rightarrow {F_{hd}}\; = {\rm{ }}1470{\rm{ }}\left( N \right) \end{array}\)

Cho biết chu kì chuyển động của Mặt Trăng quanh Trái Đất là 27,32 ngày và khoảng cách từ Trái Đất đến Mặt Trăng là 3,84.10⁸ m. Hãy tính khối lượng của Trái Đất Giả thiết quỹ đạo của Mặt Trăng là tròn. 

Phương pháp giải

Tính khối lượng của Trái Đất theo công thức:

\(M = \frac{{4{\pi ^2}{r^3}}}{{{T^2}G}} \)

Hướng dẫn giải

Gọi M và m lần lượt là khối lượng của Trái Đất và của Mặt Trăng, r là bán kính quỹ đạo của Mặt Trăng

- Ta có : 

\(\begin{array}{l} {F_{hd}} = {F_{ht}}\\ = > \frac{{GMm}}{{{r^2}}} = m{\omega ^2}r\\ = > M = \frac{{{\omega ^2}{r^3}}}{G} \end{array}\)

- Thay \(\omega = \frac{{2\pi }}{T}\) vào ta được:

\(M = \frac{{4{\pi ^2}{r^3}}}{{{T^2}G}} = \frac{{4.{{(3,14)}^2}.{{(3,84)}^3}{{.10}^{24}}}}{{{{(27,32)}^2}.{{(864)}^2}{{.10}^4}.6,{{67.10}^{ - 11}}}} \approx 6,{00.10^{24}}(kg)\)

Một vệ tinh khối lượng 100 kg được phóng lên quỹ đạo quanh Trái Đất ở độ cao mà tại đó nó có trọng lượng 920 N. Chu kì của vệ tinh là 5,3.10³ s.

a) Tính lực hướng tâm tác dụng lên vệ tinh.

b) Tính khoảng cách từ bề mặt Trái Đất đến vệ tinh. 

Phương pháp giải

a) Tính lực hướng tâm theo công thức:  F_ht = P=mg

b) Tính khoảng cách theo công thức:  h = r – R 

Với \(r = \frac{{920.{T^2}}}{{m.4{\pi ^2}}} \)

Hướng dẫn giải

a) F_ht = P = 920 N

b) F_ht = mω²r = 920 N

=>  \(r = \frac{{920.{T^2}}}{{m.4{\pi ^2}}} = \frac{{920.{{(5,3)}^2}{{.10}^6}}}{{100.4.{{(3,14)}^2}}} = 65,{53.10^5}m = 6553km\)

 Do đó h = r – R = 6553 – 6400 = 153 km

Trong môn quay tạ, một vận động viên quay dây sao cho cả dây và tạ chuyển động gần như tròn đều trong mặt phẳng nằm ngang. Muốn tạ chuyển động trên đường tròn bán kính 2,0 m với tốc độ dài 2,0 m/s thì người ấy phải giữ dây với một lực bằng 10 N. Hỏi khối lượng của tạ bằng bao nhiêu? 

Phương pháp giải

Áp dụng công thức:

\(\begin{array}{l} m = \frac{{Fr}}{{{v^2}}} \end{array}\)để tính khối lượng của tạ

Hướng dẫn giải

Lực giữ dây của vận động viên đóng vai trò là lực hướng tâm:

\(\begin{array}{l} {F_{ht}} = F = \frac{{m{v^2}}}{r}\\ = > m = \frac{{Fr}}{{{v^2}}} = \frac{{10.2}}{{{2^2}}} = 5(kg) \end{array}\)

Một quả cầu khối lượng 0,50 kg được buộc vào đầu của một sợi dây dài 0,50 m rồi quay dây sao cho quả cầu chuyển động tròn đều trong mặt phẳng nằm ngang và sợi dây làm thành một góc 30° so với phương thẳng đứng (H.14.1). Lấy g = 9,8 m/s². Xác định tốc đô dài của quả cầu.

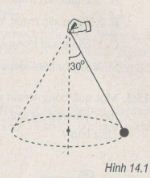
Phương pháp giải

Từ hình vẽ và công thức tính lực hướng tâm, ta tính tốc độ theo công thức:

\(v = \sqrt {gl\sin \alpha tan\alpha }\)

Hướng dẫn giải

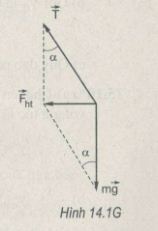
Từ hình vẽ ta có

F_ht  = mgtanα

Mà :

\(\begin{array}{l} {F_{ht}} = \frac{{m{v^2}}}{r} = \frac{{m{v^2}}}{{l\sin \alpha }}\\ \Rightarrow \frac{{m{v^2}}}{{l\sin \alpha }} = mg\tan \alpha \\ \Rightarrow v = \sqrt {gl\sin \alpha tan\alpha } \\ = \sqrt {\frac{{9,8.0,5.0,5}}{{\sqrt 3 }}} = 1,189 \approx 1,19(m/s) \end{array}\)

Một ô tô khối lượng 2,5 tấn chuyển động qua một cầu vượt với tốc độ không đổi là 54 km/h. Cầu vượt có dạng một cung tròn, bán kính 100 m. Tính áp lực của ô tô lên cầu tại điểm cao nhất của cầu. Lấy g = 9,8 m/s². 

Phương pháp giải

Áp dụng công thức:

\(\begin{array}{l} N = m\left( {g - \frac{{{v^2}}}{r}} \right)\\ \end{array}\) để tính áp lực của ô tô

Hướng dẫn giải

Ta có:

\(\begin{array}{l} {F_{ht}} = {\rm{ }}mg - N = \frac{{m{v^2}}}{r}\\ \Rightarrow N = m\left( {g - \frac{{{v^2}}}{r}} \right)\\ = 2500\left( {9,8 - \frac{{{{15}^2}}}{{100}}} \right) = 18875(N) \end{array}\)

Vậy áp lực của ô tô lên cầu tại điểm cao nhất là 18875N