Giải bài tập SBT Vật Lí 10 Bài 37: Các hiện tượng bề mặt của chất lỏng
Để các em có thêm nhiều tài liệu tham khảo hữu ích chúng tôi xin giới thiệu đến các em học sinh nội dung giải bài tập SBT môn Vật Lý 10 dưới đây. Tài liệu được eLib biên soạn và tổng hợp với nội dung các bài tập có phương pháp và hướng dẫn giải đầy đủ chi tiết, rõ ràng. Mời các em cùng tham khảo.
Mục lục nội dung
1. Giải bài 37.1 trang 79 SBT Vật lý 10
2. Giải bài 37.2 trang 79 SBT Vật lý 10
3. Giải bài 37.3 trang 80 SBT Vật lý 10
4. Giải bài 37.4 trang 80 SBT Vật lý 10
5. Giải bài 37.5 trang 80 SBT Vật lý 10
6. Giải bài 37.6 trang 80 SBT Vật lý 10
7. Giải bài 37.7 trang 80 SBT Vật lý 10
8. Giải bài 37.8 trang 80 SBT Vật lý 10

1. Giải bài 37.1 trang 89 SBT Vật lý 10
Một vòng nhôm mỏng có đường kính 50 mm và trọng lượng P = 68.10-3 N, được treo vào một lực kế lò xo sao cho đáy vòng nhôm tiếp xúc với mặt nước. Cho biết hệ số lực căng bể mặt của nước là 72.10-3 N/m. Xác định lực kéo để có thể bứt vòng nhôm lên khỏi mặt nước.
A. F = 1,13.10-3 N
B. F = 9,06.10-2N
C. F = 226.10-3 N
D. F = 7,2.10-2 N
Phương pháp giải
- Áp dụng công thức:
\(\begin{array}{l} {F_c} = 2\sigma .L = 2\sigma .\pi d\\ \end{array}\) để tính lực căng dây
- Tính lực kéo để có thể bứt vòng nhôm theo công thức:
\(\begin{array}{l} F = P + {F_c}\\ \end{array}\)
Hướng dẫn giải
- Ta có:
\(\begin{array}{l} {F_c} = 2\sigma .L = 2\sigma .\pi d\\ = {2.72.10^{ - 3}}.\pi {.50.10^{ - 3}} = {7,2.10^{ - 3}}\pi N \end{array}\)
- Lực kéo để có thể bứt vòng nhôm lên khỏi mặt nước là:
\(\begin{array}{l} F = P + {F_c}\\ = {7,2.10^{ - 3}}\pi + {68.10^{ - 3}} = {9,06.10^{ - 2}}N \end{array}\)
- Chọn đáp án B
2. Giải bài 37.2 trang 89 SBT Vật lý 10
Một màng xà phòng được căng trên mặt khung dây đồng hình chữ nhật treo thẳng đứng, đoạn dây ab dài 80 mm có thể trượt không ma sát trên khung này (H.37.1). Cho biết hệ số căng bề mặt của nước xà phòng là 40.10-3 N/m và khối lượng riêng của đồng là 8,9.103 kg/m3. Xác định đường kính của đoạn dây ab để nó nằm cân bằng, lấy g ≈ 9,8 m/s2.
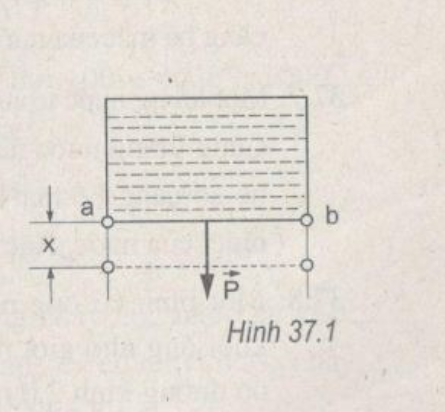
A. d = 10,8 mm.
B. d = 12,6 mm.
C. d = 2,6 mm.
D. d = 1,08 mm.
Phương pháp giải
- Áp dụng công thức:
\(\begin{array}{l} {F_c} = 2\sigma .L \end{array}\) để tính lực căng dây
- Tính đường kính của đoạn dây theo công thức:
\(d = \sqrt {\frac{{4P}}{{\rho \pi \ell g}}} \)
Hướng dẫn giải
- Lực căng màng xà phòng tác dụng lên đoạn dây ab là:
\(\begin{array}{l} {F_c} = 2.\sigma .L\\ = {2.40.10^{ - 3}}{.80.10^{ - 3}} = {6,4.10^{ - 3}}N \end{array}\)
- Dây ab nằm cân bằng khi:
\(P = {F_c} = {6,4.10^{ - 3}}N\)
- Trọng lực của dây ab là:
\(\begin{array}{l} P = mg = \rho Vg = \rho \frac{{\pi {d^2}}}{4}.\ell .g\\ \Rightarrow d = \sqrt {\frac{{4P}}{{\rho \pi \ell g}}} = \sqrt {\frac{{{{4.6,4.10}^{ - 3}}}}{{{{8,9.10}^3}.\pi {{.80.10}^{ - 3}}.9,8}}} \\ = {1,08.10^{ - 3}}m = 1,08mm \end{array}\)
- Chọn đáp án D
3. Giải bài 37.3 trang 90 SBT Vật lý 10
Một ống nhỏ giọt dựng thẳng đứng bên trong đựng nước. Nước dính hoàn toàn miệng ống và đường kính miệng dưới của ống là 0,43 mm. Trọng lượng mỗi giọt nước rơi khỏi miệng ống là 9,72. 10-5 N. Tính hệ số căng mặt của nước.
A. Xấp xỉ 72.10-3 N/m.
B. Xấp xỉ 36.10-3 N/m.
C. Xấp xỉ 72. 10-5 N/m.
D. Xấp xỉ 13,8.102 N/m.
Phương pháp giải
Tính hệ số căng bề mặt theo công thức:
\(\sigma = \frac{P}{{\pi d}}\)
Hướng dẫn giải
- Khi giọt nước rơi khỏi miệng ống thì trọng lượng P của nó bằng lực căng bề mặt Fc tác dụng lên giọt nước tại miệng ống:
\(P = {F_c} = \sigma \pi d\)
Với d là đường kính miệng ống nhỏ giọt, σσlà hệ số căng bề mặt của nước
- Từ đó suy ra:
\(\sigma = \frac{P}{{\pi d}} = \frac{{{{9,72.10}^{ - 5}}}}{{{{3,14.0,43.10}^{ - 3}}}} \approx {72.10^{ - 3}}N/m\)
- Chọn đáp án A
4. Giải bài 37.4 trang 90 SBT Vật lý 10
Một vòng nhôm mỏng có đường kính 50 mm được treo vào một lực kế lò xo sao cho đáy vòng nhôm tiếp xúc với mặt nước. Hệ số lực căng bề mặt của nước là 72.10-3 N/m. Khi vòng nhôm vừa bị kéo bứt ra khỏi mặt nước thì lực kế chỉ
A. F = 1,13.10-2 N
B. F = 2,26.10-2N
C. F = 22,6.10-2 N
D. F = 7,2.10-2 N
Phương pháp giải
Áp dụng công thức:
\(F = {F_c} = 2\sigma .L = 2\sigma .\pi d\) để tính số đo lực kế
Hướng dẫn giải
- Ta có:
\(\begin{array}{l} F = {F_c} = 2\sigma .L = 2\sigma .\pi d\\ = {2.72.10^{ - 3}}.\pi {.50.10^{ - 3}} = {2,26.10^{ - 2}}mm \end{array}\)
- Chọn đáp án B
5. Giải bài 37.5 trang 90 SBT Vật lý 10
Một màng xà phòng căng trên một khung dây đồng hình chữ nhật treo thẳng đứng (H.37.2). Đoạn dây ab dài 50 mm và có thể trượt dễ dàng trên khung. Hệ số căng bề mặt của xà phòng là 0,04 N/m. Dây ab sẽ đứng yên khi trọng lượng của nó là
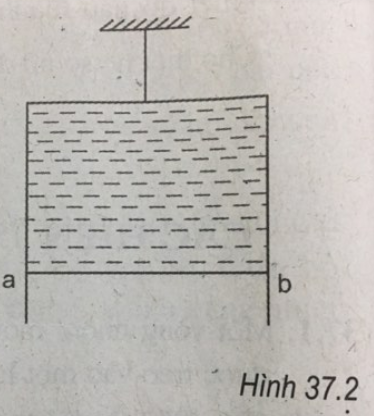
A. 2.10−3N
B. 4.10−3N
C. 1,6.10−3N
D. 2,5.10−3N
Phương pháp giải
Áp dụng công thức:
\(P = {F_c} = 2\sigma .L = 2\sigma .\pi d\) để tính trọng lượng của dây
Hướng dẫn giải
- Ta có:
\(\begin{array}{l} P = {F_c} = 2\sigma L = 2\sigma .\pi d\\ = {2.0.04.50.10^{ - 3}} = {4.10^{ - 3}}N \end{array}\)
- Chọn đáp án B
6. Giải bài 37.6 trang 90 SBT Vật lý 10
Một vòng nhôm có trọng lượng là 62,8.10-3 N được đặt sao cho đáy của tiếp xúc với mặt chất lỏng đựng trong một cốc thuỷ tinh. Đường kính trong và đường kính ngoài của vòng nhôm lần lượt bằng 48 mm và 50 mm. Cho biết hệ số căng bề mặt của nước là 72.10-3 N/m và của rượu là 22.10-3 N/m. Xác định lực kéo vòng nhôm đê bứt nó lên khỏi mặt thoáng của chất lỏng trong hai trường hợp :
a) chất lỏng là nước ;
b) chất lỏng là rượu.
Phương pháp giải
- Áp dụng công thức: Fc = σπ(d + D) để tính lực căng bề mặt
- Tính lực kéo vòng nhôm theo công thức:
F1= P + σπ(d + D) ( với mỗi hệ số căng bề mặt của các chất trong câu a, b)
Hướng dẫn giải
- Muốn kéo vòng nhôm bứt khỏi mặt thoáng của nước thì cần tác dụng lên nó lực F1 hướng thẳng đứng lên trên và có cường độ nhỏ nhất bằng tổng trọng lực P của vòng nhôm và lực căng bề mặt Fc của nước : F1 = P + Fc
- Vì mặt thoáng của nước tiếp xúc với cả mặt trong và mặt ngoài của vòng nhôm nên lực căng bề mặt Fc có độ lớn bằng :
Fc = σπ(d + D)
Từ đó suy ra: F1= P + σπ(d + D).
a) Với chất lỏng là nước có σ = 72.10-3 N/m, ta tìm được :
F1 = 62,8.10-3 + 72.10-3.3,14.(48 + 50). 10-3 ≈ 85.10-3 N
b) Với chất lỏng là rượu có σ = 22.10-3 N/m, ta tìm được :
F2 = 62,8.10-3 + 22.10-3.3,14.(48 + 50).10-3 ≈ 69,5.10-3 N.
7. Giải bài 37.7 trang 90 SBT Vật lý 10
Một mẩu gỗ hình lập phương có khối lượng 20 g được đặt nổi trên mặt nước. Mẩu gỗ có cạnh dài 30 mm và dính ướt nước hoàn toàn. Cho biết nước có khối lượng riêng là 1000 kg/m3 và hệ số căng bề mặt là 0,072 N/ Lấy g = 9,8 m/s2. Xác định độ ngập sâu trong nước của mẩu gỗ.
Phương pháp giải
- Điều kiện để mẫu gỗ nổi được tính theo công thức:
P + Fc = FA
- Độ ngập được tính theo công thức:
\(\begin{array}{l} x = \frac{{mg + \sigma 4a}}{{D{a^2}g}} \end{array}\)
Hướng dẫn giải
- Do mẩu gỗ bị nước dính ướt hoàn toàn, nên lực căng bề mặt Fc tác dụng lên mẩu gỗ hướng thẳng đứng xuống dưới. Điều kiện để mẩu gỗ nổi trên mặt nước là tổng của trọng lực Pp và lực căng bề mặt Fc phải cân bằng với lực đẩy Ác-si-mét FA (H.37.1G):
P + Fc = FA
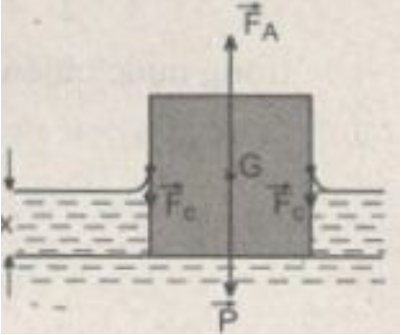
- Gọi a là độ dài mỗi cạnh của mẩu gỗ, x là độ ngập sâu trong nước của mẩu gỗ, D và σ là khối lượng riêng và hệ số căng bề mặt của nước. Thay P = mg, Fc = σ4a và FA = Da2xg (bằng trọng lượng nước bị phần mẩu gỗ chìm trong nước chiếm chỗ), ta tìm được:
\(\begin{array}{l} mg + \sigma 4a = D{a^2}xg\\ \Rightarrow x = \frac{{mg + \sigma 4a}}{{D{a^2}g}} \end{array}\)
Thay số:
\(\begin{array}{l} x = \frac{{{{20.10}^{ - 3}}.9,8 + {{0,072.4.30.10}^{ - 3}}}}{{1000.{{\left( {{{30.10}^{ - 3}}} \right)}^2}.9,8}}\\ \approx \left( {2,2 + 0,1} \right)cm = 2,3cm \end{array}\)
- Như vậy lực dính ướt có tác dụng làm mẩu gỗ chìm sâu thêm 0,1 cm chiếm tỉ lệ khoảng hơn 4% độ ngập sâu của mẩu gỗ.
8. Giải bài 37.8 trang 90 SBT Vật lý 10
Một chiếc kim hình trụ bằng thép có bôi một lớp mỏng dầu nhờn ở mặt ngoài được đặt nằm ngang và nổi trên mặt nước. Hãy xác định đường kính lớn nhất của chiếc kim sao cho độ chìm sâu trong nước của chiếc kim bằng bán kính của nó. Đường kính chiếc kim bằng 5% độ dài của nó. Cho biết khối lượng riêng của thép là 7800 kg/m3 và của nước là 1000 kg/m3 hệ số căng bề mặt của nước là 0,072 N/m, lấy g ≈ 9,8 m/s2.
Phương pháp giải
- Tính trọng lượng, lực căng và lực đẩy Ác-si-met theo các công thức sau:
\(P = mg = D\frac{{\pi {d^2}}}{4}\lg ;{F_c} = \sigma 2\left( {d + l} \right)\); \({F_A} = {D_0}\frac{1}{2}\frac{{\pi {d^2}}}{4}\lg \)
- Áp dụng công thức:
\({d_{\max }} = \sqrt {\frac{{16,8\sigma }}{{\pi g\left( {2D - {D_0}} \right)}}} \) để tính đường kính lớn nhất của chiếc kim
Hướng dẫn giải
Muốn chiếc kim nổi trên mặt nước thì hiệu số giữa trọng lượng P và lực đẩy Ác-si-mét FA tác dụng lên chiếc kim phải lớn hơn hoặc bằng lực căng bề mặt Fc của phần mặt nước đỡ chiếc kim nổi trên nó (H.37.2G) :
P – FA > Fc
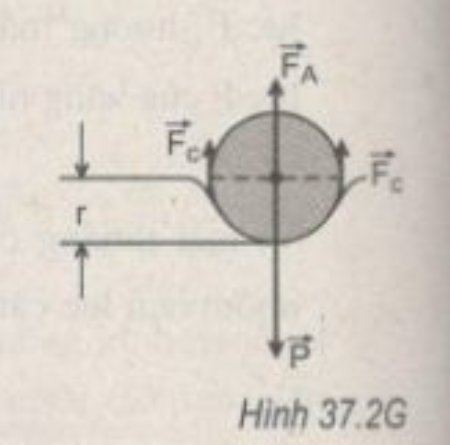
Gọi d là bán kính, l là chiều dài và D là khối lượng riêng của chiếc kim, còn D0 và σ là khối lượng riêng và hệ số căng bề mặt của nước.
Thay: \(P = mg = D\frac{{\pi {d^2}}}{4}\lg ,{F_c} = \sigma 2\left( {d + l} \right)\)
và \({F_A} = {D_0}\frac{1}{2}\frac{{\pi {d^2}}}{4}\lg \) (trọng lượng nước bị một nửa phần chiếc kim chìm
trong nước chiếm chỗ), đồng thời chú ý rằng d = 0,05l hay l = 20d, ta tìm được :
\(D\frac{{\pi {d^2}}}{4}20dg - {D_0}\frac{{\pi {d^2}}}{8}20dg \ge \sigma 2\left( {d + 20d} \right)\)
Từ đó suy ra : \(d \ge \sqrt {\frac{{16,8\sigma }}{{\pi g\left( {2D - {D_0}} \right)}}} \)
Thay số, ta được :
\({d_{\max }} = \sqrt {\frac{{16,8.0,072}}{{3,14.9,8.\left( {2.7800 - 1000} \right)}}} \approx 1,64mm\)
9. Giải bài 37.9 trang 91 SBT Vật lý 10
Một bình có ống nhỏ giọt ở đầu phía dưới. Rượu chứa trong bình chảy khỏi ống nhỏ giọt này thành từng giọt cách nhau 2,0 s. Miệng ống nhỏ giọt có đường kính 2,0 mm. Sau khoảng thời gian 720 s, khối lượng rượu chảy khỏi ống là 10 g. Xác định hệ số căng bề mặt của rượu. Coi rằng chỗ thắt của giọt rượu khi nó bắt đầu rơi khỏi miệng ống nhỏ giọt có đường kính bằng đường kính của ống nhỏ giọt. Lấy g = 9,8 m/s2.
Phương pháp giải
- Áp dụng công thức:
P = Fc = σl = σπd để tính trọng lượng mỗi giọt rượu
- Tính hệ số căng bề mặt của rượu theo công thức:
\(\sigma = \frac{{2Mg}}{{\pi dt}}\)
Hướng dẫn giải
- Trọng lượng P của mỗi giọt rượu khi bắt đầu rơi khỏi miệng ống nhỏ giọt có độ lớn bằng lực căng bề mặt Fc của rượu tác dụng lên chu vi của miệng ống nhỏ giọt, tức là :
P = Fc = σl = σπd
với σ là hệ số căng bề mặt của rượu và l = πd là chu vi của miệng ống nhỏ giọt.
- Gọi M là khối lượng rượu chảy khỏi miệng ống trong thời gian t. Vì hai giọt rượu kế tiếp chảy khỏi miệng ống cách nhau 2,0 s nên trọng lượng P mỗi giọt tính bằng :
\(P = \frac{{Mg}}{{\frac{t}{2}}} = \frac{{2Mg}}{t}\)
Từ đó ta tìm được:
\(\begin{array}{l} \sigma = \frac{{2Mg}}{{\pi dt}}\\ = \frac{{{{2.10.10}^{ - 3}}.9,8}}{{{{3,14.2.10}^{ - 3}}.720}} \approx {4,3.10^{ - 2}}\left( {N/m} \right) \end{array}\)
10. Giải bài 37.10 trang 91 SBT Vật lý 10
Một ống mao dẫn dài và mỏng có hai đầu đều hở được cắm thẳng đứng xuống nước sao cho toàn bộ chiều dài của ống ngập trong nước. Dùng tay bịt kín đầu dưới của ống và nhấc ống thẳng đứng lên khỏi nước. Sau đó buông nhẹ tay để đầu dưới của ống lại hở. Xác định độ cao của cột nước còn đọng trong ống. Cho biết đường kính của ống là 2,0 mm, khối lượng riêng của nước là 1000 kg/m3 và hệ số căng bể mặt của nước là 72,5.10-3 N/m, lấy g ≈ 9,8 m/s2.
Phương pháp giải
- Áp dụng công thức:
Fd = Fc = σπd để tính lực dính ướt
- Tính trọng lượng cột nước theo công thức:
\(P = mg = Dgh\frac{{\pi {d^2}}}{4}\)
- Độ cao của cột nước được tính theo công thức:
\(h = \frac{{8\sigma }}{{Dgd}}\)
Hướng dẫn giải
- Cột nước còn đọng lại được trong ống mao dẫn là do tác dụng cân bằng giữa trọng lượng P của cột nước với tổng các lực dính ướt Fd của thành ống tạo thành mặt khum lõm ở đầu trên và mặt khum lồi ở đầu dưới của cột nước (H.37.3G). Tại vị trí tiếp xúc giữa hai mặt khum của cột nước với thành ống, các lực dính ướt Fd đều hướng thẳng đứng lên phía trên và có cùng độ lớn với lực căng bề mặt Fc của nước.
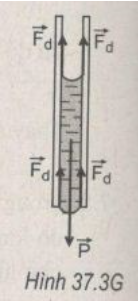
Fd = Fc = σπd
với d là đường kính của ống mao dẫn và σ là hệ số căng bề mặt của nước. Nếu gọi D là khối lượng riêng của nước và h là độ cao của cột nước trong ống thì trọng lượng cột nước bằng:
\(P = mg = Dgh\frac{{\pi {d^2}}}{4}\)
- Khi đó điều kiện cân bằng của cột nước đọng lại trong ống là :
\(P = 2{F_d} = > Dgh\frac{{\pi {d^2}}}{4} = 2\sigma \pi d\)
Từ đó suy ra:
\(\begin{array}{l} h = \frac{{8\sigma }}{{Dgd}}\\ = \frac{{{{8.72.10}^{ - 3}}}}{{{{1000.9,8.2,0.10}^{ - 3}}}} \approx 29,4\left( {mm} \right) \end{array}\)
Tham khảo thêm
- doc Giải bài tập SBT Vật Lí 10 Bài 34 - 35: Chất rắn kết tinh. Chất rắn vô định hình. Biến dạng cơ của vật rắn
- doc Giải bài tập SBT Vật Lí 10 Bài 36: Sự nở vì nhiệt của vật rắn
- doc Giải bài tập SBT Vật Lí 10 Bài 38: Sự chuyển thể của các chất
- doc Giải bài tập SBT Vật Lí 10 Bài 39: Độ ẩm của không khí
- doc Giải bài tập SBT Vật Lí 10 Bài tập cuối chương VII: Chất rắn-chất lỏng. Sự chuyển thể
