Giải bài tập SBT Vật Lí 10 Bài 9: Tổng hợp và phân tích lực. Điều kiện cân bằng của chất điểm

Một chất điểm đứng yên dưới tác dụng của ba lực 4 N, 5 N và 6 N. Nếu bỏ đi lực 6 N thì hợp lực của hai lực còn lại bằng bao nhiêu ?

A. 9 N.

B. 1 N.

C. 6N.

D. Không biết vì chưa biết góc giữa hai lực còn lại. 

Phương pháp giải

Muốn cho một chất điểm đứng cân bằng thì hợp lực của các lực tác dụng lên nó bằng không

Hướng dẫn giải

- Theo đề bài, vật đứng yên (cân bằng) dưới tác dụng của 3 lực 4N, 5N và 6N nên theo điều kiện cân bằng của chất điểm ta có hợp lực của 3 lực 4N, 5N và 6N bằng 0. Suy ra hợp lực của hai lực 4N và 5N cân bằng với lực 6 N

- Chọn đáp án C

Một chất điểm đứng yên dưới tác dụng của ba lực 6 N, 8 N và 10 N. Hỏi góc giữa hai lực 6 N và 8 N bằng bao nhiêu ?

A. 30°.                                     B. 60°.

C. 45°.                                     D. 90°. 

Phương pháp giải

- Muốn cho một chất điểm đứng cân bằng thì hợp lực của các lực tác dụng lên nó bằng không.

- Nếu hai lực đồng qui làm thành hai cạnh của một hình bình hành, thì đường chéo kẻ từ điểm đồng qui biểu diễn hợp lực của chúng

Hướng dẫn giải

- Theo đề bài, vật đứng yên (cân bằng) dưới tác dụng của 3 lực 6N, 8N và 10N nên theo điều kiện cân bằng của chất điểm ta có hợp lực của 3 lực 6N, 8N và 10N bằng 0.

Suy ra hợp lực của hai lực 6N và 8N cân bằng với lực 10N

- Ta có: 6²+8²=10²

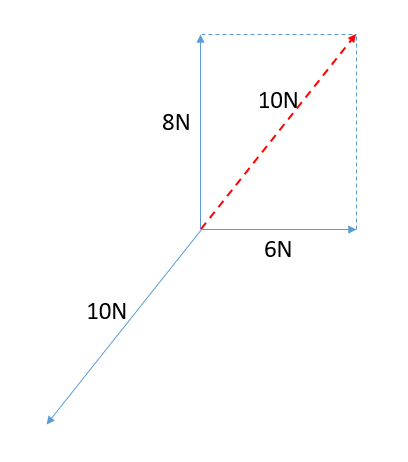
Góc hợp bởi hai lực 6N và 8N là 900

- Chọn đáp án D

Lực 10 N là hợp lực của cặp lực nào dưới đây ? Cho biết góc giữa cặp lực đó.

A. 3 N, 15 N ; 120°.                 B. 3 N, 13 N ; 180°.

C. 3 N, 6 N ; 60°.                     D. 3 N, 5 N ; 0°. 

Phương pháp giải

Sử dụng lí thuyết về qui tắc tổng hợp lực (qui tắc hình bình hành) và định lí cos trong tam giác

- Nếu hai lực đồng qui làm thành hai cạnh của một hình bình hành, thì đường chéo kẻ từ điểm đồng qui biểu diễn hợp lực của chúng

- Định lí cos: \({a^2} = {b^2} + {c^2} - 2bc.\cos \beta \)$$

Hướng dẫn giải

- Áp dụng qui tắc hình bình hành ta có hình vẽ

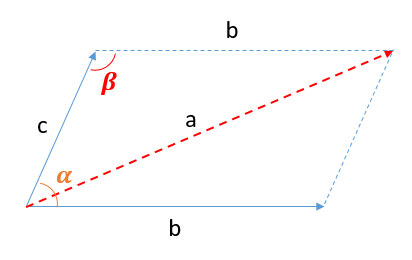
- Áp dụng định lí cos trong tam giác có: 

\({a^2} = {b^2} + {c^2} - 2bc.\cos \beta \)

- Thử 4 đáp án A,B,C và D vào phương trình (*) ta có: 

\({3^2} + {13^2} + 2.3.13.\cos 180 = 100 = {10^2}\)

- Lực 10 N là hợp lực của cặp lực 3 N, 13 N ; 180°. 

- Chọn đáp án B

Câu nào đúng ?

Hợp lực của hai lực có độ lớn F và 2F có thể 

A. nhỏ hơn F.

B. lớn hơn 3F.

C. vuông góc với lực F.

D. vuông góc với lực 2F. 

Phương pháp giải

Sử dụng quy tắc hợp lực để trả lời câu hỏi này

Hướng dẫn giải

- Hợp lực của hai lực có độ lớn F và 2F có thể vuông góc với lực F.

- Chọn đáp án C

Một vật có khối lượng m = 5,0 kg được treo bằng ba dây (H.9.1). Lấy g = 9,8 m/s². Tìm lực kéo của dây AC và dây BC.

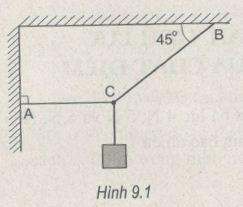
Phương pháp giải

Tìm lực kéo của dây AC và dây BC theo công thức:

\(\begin{array}{l} {F_1} = P' ; {F_2} = P'\sqrt 2 \end{array}\)

Hướng dẫn giải

Hợp lực cân bằng với trọng lực của vật.

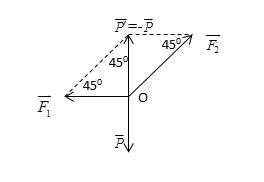
Từ hình vẽ ta có

P’ = P = mg = 5,0.9,8 = 49 N.

\(\begin{array}{l} \frac{{P'}}{P} = \tan {45^0} = 1\\ = > {F_1} = P' = 49(N)\\ \frac{{P'}}{{{F_2}}} = \cos {45^0} = \frac{{\sqrt 2 }}{2}\\ \Rightarrow {F_2} = P'\sqrt 2 \approx 49.1,41 \approx 70(N) \end{array}\)

Một đèn tín hiệu giao thông được treo ở một ngã tư nhờ một dây cáp có trọng lượng không đáng kể. Hai đầu dây cáp được giữ bằng hai cột đèn AB và A'B', cách nhau 8 m. Đèn nặng 60 N, được treo vào điểm giữa O của dây cáp, làm dây võng xuống 0,5 m tại điểm giữa (H.9.2). Tính lực kéo của mỗi nửa dây.

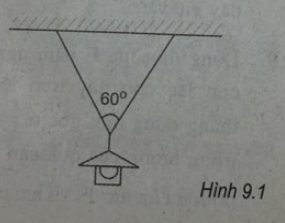
Phương pháp giải

Phân tích lực và tính lực kéo theo công thức:

\(\begin{array}{l} {F_1} = \frac{{P\sqrt {A{B^2} + O{A^2}} }}{{2AB}} \end{array}\)

Hướng dẫn giải

Điểm O coi là điêm đứng cân bằng dưới tác dụng của ba lực: trọng lực và hai lực kéo và của hai nửa dây cáp như hình vẽ

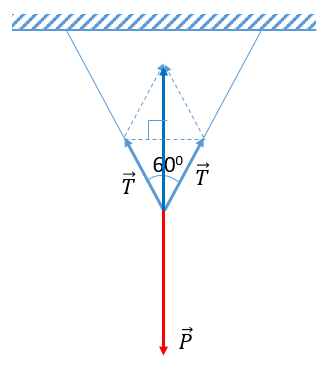
Từ hai tam giác đồng dạng ta có: 

\(\begin{array}{l} \frac{{{F_1}}}{{\frac{F}{2}}} = \frac{{OA}}{{AB}}\\ = > \frac{{2{F_1}}}{P} = \frac{{OA}}{{AB}}\\ = > {F_1} = \frac{{P\sqrt {A{B^2} + O{A^2}} }}{{2AB}} = \frac{{60\sqrt {0,25 + 16} }}{{2.0,5}} = 241,86 \approx 242(N) \end{array}\)

Một vật có trọng lượng P = 15 N được giữ yên trên một mặt phẳng nghiêng không ma sát bằng một dây song song với mặt phẳng nghiêng (H.9.3). Góc nghiêng a = 30°. Cho biết mặt phẳng nghiêng tác dụng lên vật một lực theo phương vuông góc với mặt phẳng nghiêng. Tìm lực của dây giữ vật.

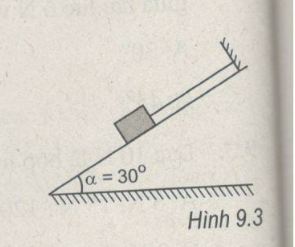
Phương pháp giải

Phân tích lực và tính lực căng dây theo công thức:

\(\begin{array}{l} F = P'.0,5 \end{array}\)

Hướng dẫn giải

Vật chịu tác dụng của ba lực cân bằng như hình vẽ:

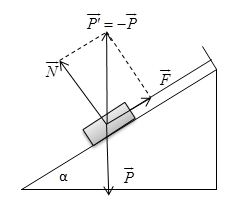
\(\begin{array}{l} \vec P + \vec N + \vec F = \vec 0\\ \Rightarrow \vec N + \vec F = - \vec P = \overrightarrow {P'} \end{array}\)

Từ tam giác lực ta có:

\(\begin{array}{l} \frac{F}{{P'}} = \sin {30^0} = 0,5\\ \Rightarrow F = P'.0,5 = P.0,5 = 7,5(N) \end{array}\)

Dùng một lực F nằm ngang kéo quả cầu con lắc cho dây treo lệch khỏi phương thẳrig đứng một góc a = 30° (H.9.4). Biết trọng lượng của quả cầu là 20 N, hãy tính lực F và lực căng T của dây.

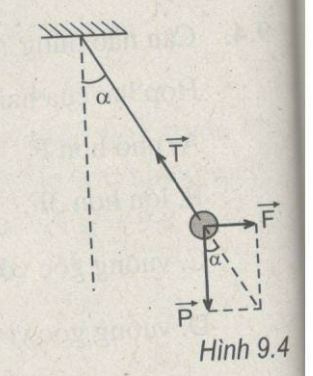
Phương pháp giải

Phân tích lực và tính lực theo công thức:

\(\begin{array}{l} F = P'\tan \alpha = P\tan \alpha ;T = 2F \end{array}\)

Hướng dẫn giải

Do quả cầu nằm cân bằng dưới tác dụng của ba lực nên ta có:

\(\begin{array}{l} \vec P + \vec F + \vec T = \vec 0\\ \Rightarrow \vec F + \vec T = - \vec P = \overrightarrow {P'} \end{array}\)

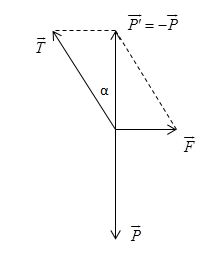
Từ hình vẽ ta có:

\(\begin{array}{l} F = P'\tan \alpha = P\tan \alpha = 20.\frac{1}{{\sqrt 3 }} \approx 11,5(N)\\ T = 2F{\rm{ }} \approx {\rm{ }}23{\rm{ }}N \end{array}\)

Người ta giữ một vật có trọng lượng 20 N đứng yên trên một mặt phẳng nghiêng không ma sát, có góc nghiêng a = 45° (H.9.5). Cho biết lực mà mặt phẳng nghiêng tác dụng lên vật có phương vuông góc với mặt phẳng nghiêng. Tìm lực đẩy ngang F và lực của mặt phẳng nghiêng tác dụng lên vật.

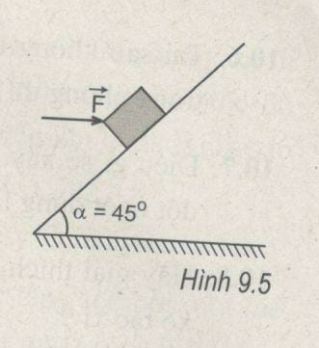
Phương pháp giải

Phân tích lực và tính lực đẩy, phản lực theo công thức:

\(P = F ;N = P\sqrt 2 \)

Hướng dẫn giải

Điều kiện cân bằng của vật: 

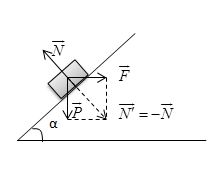
Từ tam giác lực ta có được:

\(P = F = 20{\rm{ }}N;{\rm{ }}N = P\sqrt 2 \approx 28(N)\)