Giải bài tập SBT Vật Lí 10 Bài 19: Quy tắc hợp lực song song cùng chiều

Hai người cùng khiêng một thanh dầm bằng gỗ nặng, có chiều dài L. Người thứ hai khoẻ hơn người thứ nhất. Nếu tay của người thứ nhất nâng một đầu thanh thì tay của người thứ hai phải đặt cách đầu kia của thanh một đoạn bằng bao nhiêu để người thứ hai chịu lực lớn gấp đôi người thứ nhất ?

A. L/3.                B. L/4.          

C. 2L/5.               D. 0 

Phương pháp giải

Tính khoảng cách theo công thức:

\({\frac{{{F_2}}}{{{F_1}}} = \frac{{OA}}{{OC}}\,\,và\,\,OB = 2.OC}\)

Hướng dẫn giải

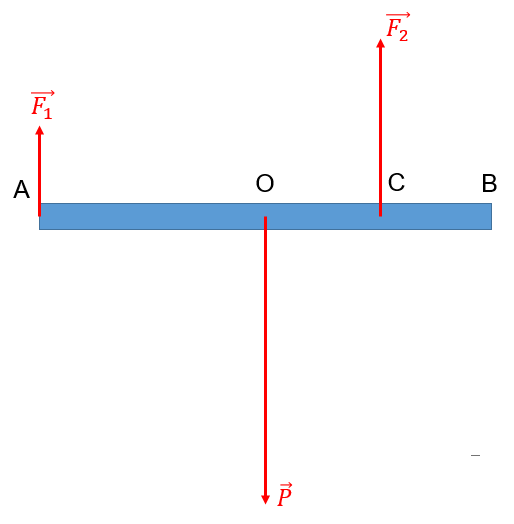
- Ta có:

\(\begin{array}{l} \frac{{{F_2}}}{{{F_1}}} = \frac{{OA}}{{OC}} = 2\\ OB = 2.OC \Rightarrow CB = \frac{{AB}}{4} = \frac{L}{4} \end{array}\)

⇒ Tay của người thứ hai phải đặt cách đầu kia của thanh một đoạn bằng L/4 để người thứ hai chịu lực lớn gấp đôi người thứ nhất 

- Chọn đáp án B

Một thanh cứng có trọng lượng không đáng kể, được treo nằm ngang nhờ hai lò xo thẳng đứng có chiều dài tự nhiên bằng nhau (H.19.1). Độ cứng của hai lò xo lần lượt là k₁=150 N/m và k₂=100 N/m. Khoảng cách AB giữa hai lò xo là 75 cm. Hỏi phải treo một vật nặng vào điểm C cách đầu A bao nhiêu để thanh vẫn nằm ngang ?

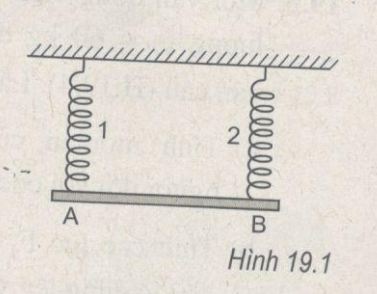
A. 45 cm.          B. 30 cm.        

C. 50 cm.         D. 25 cm. 

Phương pháp giải

Tính OA từ tỉ số:

\(\frac{{OC}}{{OA}} = \frac{{{k_1}}}{{{k_2}}}\)

Hướng dẫn giải

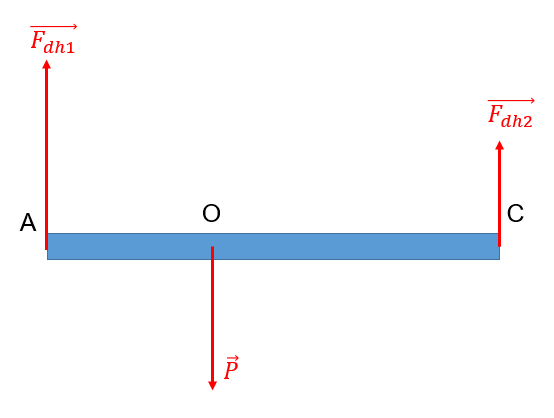
- Ta có:

\(\begin{array}{l} + \,\,\frac{{{F_{dh1}}}}{{{F_{dh2}}}} = \frac{{OC}}{{OA}} = \frac{{{k_1}.{\rm{\Delta }}{x_1}}}{{{k_2}.{\rm{\Delta }}{x_2}}}\\ {\rm{ + }}\,\,{\rm{\Delta }}{x_1} = {\rm{\Delta }}{x_2}\\ \Rightarrow \frac{{OC}}{{OA}} = \frac{{{k_1}}}{{{k_2}}} = \frac{{150}}{{100}} = \frac{3}{2}\\ AC = 75cm \Rightarrow OA = \frac{2}{5}.75 = 30cm \end{array}\)

⇒ Phải treo một vật nặng vào điểm C cách đầu A 30 cm thì thanh vẫn nằm ngang 

- Chọn đáp án B

Hai người cầm hai đầu một chiếc gậy để khênh một vật nặng. Gậy có trọng lượng không đáng kể, dài 1,4 m. Vật có trọng lượng 700 N được treo vào điểm c cách tay người ở đầu A của thanh 0,6 m. Hỏi tay người ở đầu B chịu một lực bằng bao nhiêu?

A. 400 N.         B. 525 N.        

C. 175N.         D. 300 N. 

Phương pháp giải

Tính lực tác dụng vào đầu B từ các công thức:

\(\frac{{{F_B}}}{{{F_A}}} = \frac{{{d_1}}}{{{d_2}}}\,\,\,và \,\,\,{F_A} + {F_B}\)

Hướng dẫn giải

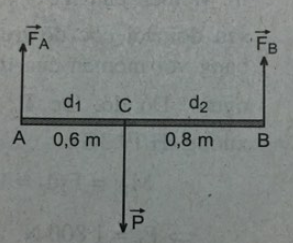
- Ta có:

\(\begin{array}{l} + \,\,\frac{{{F_B}}}{{{F_A}}} = \frac{{{d_1}}}{{{d_2}}} = \frac{{0,6}}{{0,8}} = \frac{3}{4}\\ + \,\,{F_A} + {F_B} = 700N\\ \Rightarrow {F_A} = 400N;{F_B} = 300N \end{array}\)

⇒ Người ở đầu B chịu một lực bằng 300 N. 

- Chọn đáp án D

Chiếc bị buộc ở đầu gậy cách vai 60 cm. Tay người giữ ở đầu kia cách vai 30 cm. Bỏ qua trọng lượng của gậy (H.19.2).

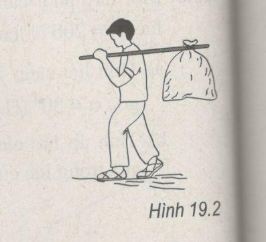
a) Hãy tính lực giữ của tay.

b) Nếu dịch chuyển gậy cho bị cách vai 30 cm và tay cách vai 60 cm, thì lực giữ bằng bao nhiêu ?

c) Trong hai trường hợp trên, vai người chịu một áp lực bằng bao nhiêu ? 

Phương pháp giải

a,b) Tính lực giữ của tay theo công thức:

F/P=d_F/d_P với mỗi giá trị d tương ứng

c) Áp lực tính theo công thức: F'= F + P

Hướng dẫn giải

a.) Lực giữ của tay là:

 \(\frac{F}{P} = \frac{{60}}{{30}} = 2 = > F = 2P = 100(N)\)

b) Lực giữ của tay là:

 \(\frac{F}{P} = \frac{{30}}{{60}} = \frac{1}{2} = > F = \frac{1}{2}P = 25(N)\)

c. Áp lực bằng F'= F + P = 150 N hoặc 75 N

Xác định các áp lực của trục lên hai ổ trục A và B (H.19.3). Cho biết trục có khối lượng 10 kg, bánh đà đặt tại C có khối lượng 20 kg, khoảng cách AC = 1 m ; BC = 0,4 m lấy g = 10 m/s²

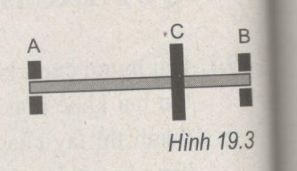
Phương pháp giải

Áp dụng quy tắc momen: M_A=M_B và công thức: M=F.d để tính các áp lực

Hướng dẫn giải

- Trọng lực của ổ trục là:

P_1A = P_1B = 0,5P = 50 N.

- Làm tương tự với trọng lực của bánh đà:

P_2A + P_2B = P₂  = 200 N   (1)

\(\frac{{{P_{2A}}}}{{{P_{2B}}}} = \frac{{0,4}}{1} = 0,4\)$\mathrm{}$   (2)

- Từ (1) và (2) ta được P_2A = 57 N và P_2B = 143 N.

- Vậy áp lực lên ổ trục A là P_1A + P_2A = 107 N

- Áp lực lên ổ trục B là P_1B + P_2B = 193 N

Một vận động viên nhảy cầu có khối lượng m = 60 kg đang đứng ở mép ván cầu (H.19.4). Lấy g = 10 m/s².

a) Tính momen của trọng lực của người đối với cọc đỡ trước.

b)  Tính các lực F₁ và F₂ mà hai cọc đỡ tác dụng lên ván.

Bỏ qua khối lượng của tấm ván.

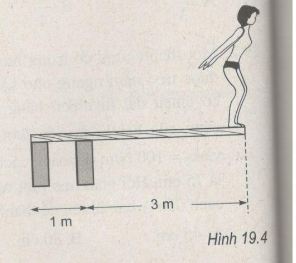
Phương pháp giải

a. Tính momen theo công thức: M=P.l

b.- Tính momen theo công thức: M=.F.d

- Hợp lực tính bằng: F₁ = F₂ + P

Hướng dẫn giải

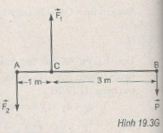
a. Momen của trọng lực của người đối với cọc là:

M = P.l = 600.3,0 = 1800 N.m

b. Momen của lực  \(\overrightarrow {{F_2}} \)$$ của cọc đỡ sau đối với cọc đỡ trước phải cân bằng với momen của trọng lực của người.

- Do đó, lực \(\overrightarrow {{F_2}} \)$$ phải hướng xuống (H.19.3G)

M_F2 = F₂d₂ = 1800 N.m

=> F₂ = 1800 N.

- Hợp lực của \(\overrightarrow {{F_2}} \) và \(\overrightarrow {{P}} \)$$ cân bằng với lực \(\overrightarrow {{F_1}} .\)$$

F₁ = F₂ + P = 2400 N.