Giải bài tập SBT Vật Lí 10 Bài tập cuối chương IV: Các định luật bảo toàn
Cùng eLib ôn tập kiến thức và rèn luyện phương pháp giải các bài tập cuối chương IV: Các định luật bảo toàn trong nội dung Hướng dẫn giải bài tập dưới đây. Hy vọng đây sẽ là tài liệu hữu ích với các em học sinh.
Mục lục nội dung
1. Giải bài IV.1 trang 63 SBT Vật lý 10
2. Giải bài IV.2 trang 63 SBT Vật lý 10
3. Giải bài IV.3 trang 63 SBT Vật lý 10
4. Giải bài IV.4 trang 63 SBT Vật lý 10
5. Giải bài IV.5 trang 64 SBT Vật lý 10
6. Giải bài IV.6 trang 64 SBT Vật lý 10
7. Giải bài IV.7 trang 64 SBT Vật lý 10
8. Giải bài IV.8 trang 64 SBT Vật lý 10
9. Giải bài IV.9 trang 64 SBT Vật lý 10
10. Giải bài IV.10 trang 65 SBT Vật lý 10

1. Giải bài IV.1 trang 63 SBT Vật lý 10
Xác định lực đẩy trung bình của hơi thuốc súng tác dụng lên một đầu đạn ở trong nòng súng trường, biết rằng đầu viên đạn có khối lượng 10 g, chuyển động trong nòng súng nằm ngang trong khoảng thời gian 0,001 s, với vận tốc đầu bằng không và vận tốc tại đầu nòng súng là 865 m/s.
A. 86,5N.
B. 8650 N.
C. 8,65 N.
D. 865 N.
Phương pháp giải
Áp dụng công thức về độ biến thiên động lượng để tính lực đẩy theo công thức:
\(F = \frac{{mv}}{{{\rm{\Delta }}t}} \)
Hướng dẫn giải
- Áp dụng công thức về độ biến thiên động lượng
\(m{\rm{\Delta }}v = m(v - {v_0}) = \vec F{\rm{\Delta }}t\)
- Vì vận tốc ban đầu bằng 0, suy ra độ lớn trung bình của lực đẩy
\(F = \frac{{mv}}{{{\rm{\Delta }}t}} = \frac{{{{10.10}^{ - 3}}.865}}{{0,001}} = 8650N\)
- Chọn đáp án B
2. Giải bài IV.2 trang 63 SBT Vật lý 10
Một quả bóng khối lượng 0,20 kg đang bay với vận tốc 5,0 m/s tới đập vuông góc với mặt bức tường thẳng đứng trong khoảng thời gian 0,1 s. Ngay sau va đập, quả bóng bị bật ngược lại với cùng độ lớn của vận tốc đầu. Xác định độ lớn của lực do bức tường tác dụng vào quả bóng khi va đập.
A. 2.0N. B. 10 N.
C. 20 N. D. 100 N.
Phương pháp giải
Áp dụng công thức về độ biến thiên động lượng để tính độ lớn lực tác dụng vào quả bóng theo công thức:
\(F = \frac{{2mv'}}{{{\rm{\Delta }}t}} \)
Hướng dẫn giải
- Áp dụng công thức về độ biến thiên động lượng
\(m{\rm{\Delta }}v = m(v - {v_0}) = \vec F{\rm{\Delta }}t\)
Chọn chiều dương là chiều của lực \(\vec F\)do bức tường tác dụng vào quả bóng. Vì các vận tốc \(\vec v\) và \(\vec v'\)của quá bóng trước và sau và đập có cùng độ lớn, nhưng hướng ngược nhau, nên v=−v′<0
\(\begin{array}{l} \Rightarrow F{\rm{\Delta }}t = mv' - mv = 2mv'\\ \Rightarrow F = \frac{{2mv'}}{{{\rm{\Delta }}t}} = \frac{{2.0,2.5}}{{0,1}} = 20N \end{array}\)
- Chọn đáp án C
3. Giải bài IV.3 trang 63 SBT Vật lý 10
Một vật khối lượng 200 g được ném thẳng đứng từ độ cao 15 m xuống đấi với vận tốc đầu là 5 m/s. Khi chạm đất, vật xuyên sâu vào đất 5 cm và nằm yên tại đó. Lấy g ≈10 m/s2. Bỏ qua lực cản của không khí. Xác định lực cản trung bình của đất tác dụng lên vật.
A. 648 N. B. 349 N.
C. 6,490 N. D. 34,9 N
Phương pháp giải
- Tính vận tốc chạm đất theo công thức:
\(v = \sqrt {2gh + v_0^2} \)
- Áp dụng công thức về độ biến thiên động năng, tính lực cản theo công thức:
\({F_c} = \frac{{m{v^2}}}{{2S}} \)
Hướng dẫn giải
- Vì vật rơi nhanh dần đều từ độ cao h = 15 m xuống đất với vận tốc đầu v0=5m/s và gia tốc g≈10m/s2, nên ta có phương trình:
v2−v20=2gh
- Suy ra vận tốc của vật ngày tước khi chạm đất bằng:
\(v = \sqrt {2gh + v_0^2} = \sqrt {2.10.15 + {5^2}} \approx 18m/s\)
- Áp dụng công thức về độ biến thiên động năng:
\(\frac{{m{v^{\prime 2}}}}{2} - \frac{{m{v^2}}}{2} = A = - {F_c}.S\)
Thay v≈18m/s; v′=0 lực cản trung bình của đất tác dụng lên vật là
\({F_c} = \frac{{m{v^2}}}{{2S}} = \frac{{{{200.10}^{ - 3}}{{.18}^2}}}{{{{2.5.10}^{ - 2}}}} \approx 648N\)
- Chọn đáp án A
4. Giải bài IV.4 trang 63 SBT Vật lý 10
Ba quả bóng được ném đi từ cùng một độ cao với vận tốc đầu có cùng độ lớn nhưng theo ba hướng khác nhau: 1. Lên cao ; 2. Nằm ngang ; 3. Xuống thấp. Nếu gọi vận tốc của ba quả bóng ngay trước khi chạm đất là v1, v2, v3 và bỏ qua sức cản của không khí thì
A. v1>v2>v3
B.v2>v1>v3
C. v1=v2=v3
D. v3>v1>v2
Phương pháp giải
Áp dụng định luật bảo toàn cơ năng:
\({\rm{W}} = \frac{{mv_0^2}}{2} + mgh = \frac{{m{v^2}}}{2}\) để xác định tỉ lệ giữa các vận tốc
Hướng dẫn giải
- Với ba quả bóng ta đều có:
\({\rm{W}} = \frac{{mv_0^2}}{2} + mgh = \frac{{m{v^2}}}{2}\)
- Trong đó v được thay tương ứng bởi v1, v2, v3
Do đó v1=v2=v3
- Chọn đáp án C
5. Giải bài IV.5 trang 64 SBT Vật lý 10
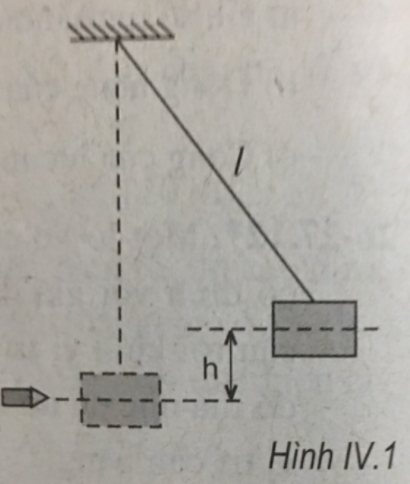
Để xác định vận tốc của đầu đạn người ta dùng con lắc thủ đạn, gồm một hộp đựng cát khối lượng M được treo vào một sợi dây l. Khi được bắn, đầu đạn khối lượng m bay theo phương nằm ngang, cắm vào cát và nâng hộp cát lên cao thêm một đoạn h so với vị trí cân bằng (H.IV.1). Vận tốc của đầu đạn là:
\(\begin{array}{l} A.\,\,\,\frac{m}{{M + m}}\sqrt {2gh} \\ B.\,\,\,\frac{m}{{M - m}}\sqrt {2gh} \\ C.\,\,\,\frac{{M + m}}{m}\sqrt {2gh} \\ D.\,\,\,\frac{{M - m}}{m}\sqrt {2gh} \end{array}\)
Phương pháp giải
Áp dụng định luật bảo toàn động lượng và định luật bảo toàn cơ năng tìm được vận tốc theo công thức:
\( v = \frac{{M + m}}{m}\sqrt {2gh} \)
Hướng dẫn giải
- Khi viên đạn va chạm mềm vào hộp cát
mv=(M+m)u(1)
- Khi viên đạn và hộp cát chuyển động lên cao
\(0 + (M + m)gh = \frac{1}{2}(M + m){u^2} + 0(2)\)
Từ (1) và (2)
\( \Rightarrow v = \frac{{M + m}}{m}\sqrt {2gh} \)
- Chọn đáp án C
6. Giải bài IV.6 trang 64 SBT Vật lý 10
Một vật khối lượng 10 kg đang đứng yên chịu tác dụng một lực 5 N theo phương ngang. Xác định :
a) Công của lực trong giây thứ nhất, giây thứ hai và giây thứ ba.
b) Công suất tức thời của lực tại giây thứ tư. Cho biết công suất tức thời tính theo công thức : P = Fv, với F là lực tác dụng và v là vận tốc tức thời của vật.
Phương pháp giải
a) - Áp dụng công thức: a=F/m để tính gia tốc
- Tính quãng đường theo công thức:
\(s = \frac{{a{t^2}}}{2} \) (Áp dụng cho mỗi giây)
- Công thức hiện được tính theo công thức: A=F.s
b) Tính công suất tức thời theo công thức:
P = Fv
Hướng dẫn giải
a) Gia tốc của vật:
a=F/m=5/10=0,5(m/s2)
Quãng đường vật dịch chuyển:
\(s = \frac{{a{t^2}}}{2} = \frac{{0,5{t^2}}}{2} = 0,25{t^2}\)
Công của lực thực hiện: A = Fs.
- Trong giây thứ nhất (từ 0 đến 1s):
\({s_1} = 0,25t_1^2 = 0,25\left( {{1^2} - 0} \right) = 0,25(m)\)
Suy ra: A1 = Fs1 = 5.0,25 = 1,25 J.
- Trong giây thứ 2 (từ 1s đến 2s):
\(\begin{array}{l} {s_2} = 0,25\left( {t_2^2 - t_1^2} \right)\\ = 0,25{\left( {{2^2} - {1^2}} \right)^2} = 0,75\left( m \right) \end{array}\)
Suy ra: A2 = Fs2 = 5.0,75 = 3,75 J.
- Trong giây thứ ba (từ 2s đến 3s):
\(\begin{array}{l} {s_3} = 0,25\left( {t_3^2 - t_2^2} \right)\\ = 0,25\left( {{3^2} - {2^2}} \right) = 1,25(m) \end{array}\)
Suy ra: A3 = Fs3 = 5.1,25 = 6,25 J.
b) Công suất tức thời của lực: P = Fv.
Tại giây thứ tư (t = 4s): v = at = 0,2.4 = 0,8 m/s
Suy ra: P = F.v = 5.0,8 = 4 W.
7. Giải bài IV.7 trang 64 SBT Vật lý 10
Một ô tô đang chạy với vận tốc 30 km/h trên đoạn đường phẳng ngang thì hãm phanh và tiếp tục chạy thêm được quãng đường dài 10 m. Coi lực ma sát giữa lốp ô tô và mặt đường khi hãm phanh là không đổi. Nếu trước khi hãm phanh, ô tô đang chạy với vận tốc 90 km/h thì ô tô sẽ tiếp tục chạy thêm được quãng đường dài bao nhiêu ?
Phương pháp giải
- Áp dụng công thức độ biến thiên động năng:
\(\frac{{m{v^2}}}{2} - \frac{{mv_0^2}}{2} = A\)
- Lập tỉ số giữa hai quãng đường theo công thức:
\(s = \frac{{mv_0^2}}{{2{F_{ms}}}}\)
Hướng dẫn giải
- Áp dụng công thức về độ biến thiên động năng:
\(\frac{{m{v^2}}}{2} - \frac{{mv_0^2}}{2} = A\)
- Thay v = 0 và A = - Fms, ta tìm được:
\(s = \frac{{mv_0^2}}{{2{F_{ms}}}}\)
- Vì Fms và m không thay đổi, nên s tỉ lệ với v02, tức là:
\(\frac{{{s_2}}}{{{s_1}}} = {\left( {\frac{{{v_{02}}}}{{{v_{01}}}}} \right)^2} \Rightarrow {s_2} = 4.{\left( {\frac{{90}}{{30}}} \right)^2} = 36(m)\)
8. Giải bài IV.8 trang 64 SBT Vật lý 10
Một vật khối lượng 500 kg móc ở đầu sợi dây cáp của một cần cẩu và được kéo thẳng đứng từ mặt đất lên phía trên với sức căng không đổi. Khi tới độ cao 4,5 m thì vật đạt được vận tốc 0,60 m/s.
a) Xác định lực căng của sợi dây cáp. Lấy g = 9,8 m/s2.
b) Nếu sợi dây cáp chỉ chịu được lực căng tối đa là 6000 N, thì ở cùng độ cao nêu trên vật có thể đạt được vận tốc bằng bao nhiêu ?
Phương pháp giải
Áp dụng công thức độ biến thiên cơ năng:
\(\frac{{m{v^2}}}{2} + mgh = Th\)
a) Tính lực căng dây theo công thức:
\(\begin{array}{l} T = m\left( {\frac{{{v^2}}}{{2h}} + g} \right)\\ \end{array}\)
b) Tính vận tốc cực đại theo công thức:
\({v_{\max }} = \sqrt {\frac{{2h}}{m}\left( {{T_{\max }} - mg} \right)} \)
Hướng dẫn giải
a) Vật nặng chịu lực căng \(\vec T\) (ngoại lực) tác dụng, chuyển động từ mặt đất lên tới độ cao h = 10 m và đạt được vận tốc v = 0,5 m. Trong trường hợp này, độ biến thiên cơ năng của vật có giá trị bằng công do ngoại lực thực hiện, nên ta có :
\(\frac{{m{v^2}}}{2} + mgh = Th\)
Suy ra lực căng của sợi dây cáp :
\(\begin{array}{l} T = m\left( {\frac{{{v^2}}}{{2h}} + g} \right)\\ \approx 500\left( {\frac{{{{0,60}^2}}}{{2.4,5}} + 9,8} \right) = 4920(N) \end{array}\)
b) Nếu dây cáp chịu được lực căng tối đa Tmax = 6000 N > 4920 N, thì ở cùng độ cao nêu trên vật có thể đạt được vận tốc tối đa vmax sao cho :
\(\frac{{mv_{\max }^2}}{2} + mgh = {T_{\max }}h\)
Suy ra:
\(\begin{array}{l} {v_{\max }} = \sqrt {\frac{{2h}}{m}\left( {{T_{\max }} - mg} \right)} \\ = \sqrt {\frac{{2.4,5}}{{500}}\left( {6000 - 500.9,8} \right)} \approx 14(m/s) \end{array}\)
9. Giải bài IV.9 trang 64 SBT Vật lý 10
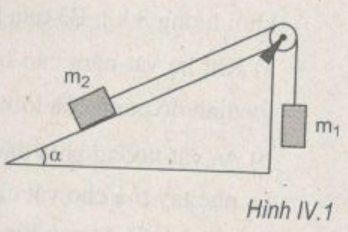
Hai vật nặng có khối lượng lần lượt là m1 = 2 kg và m2 = 1 kg được móc vào hai đầu của một sợi dây vắt ngang qua một ròng rọc : vật m1 treo thẳng đứng, vật m2 nằm trên mặt phẳng nghiêng một góc α = 30° như hình IV.l. Ban đầu hệ vật được giữ đứng yên, sau đó thả nhẹ cho hệ vật chuyển động. Bỏ qua lực ma sát, lực cản, khối lượng của ròng rọc và dây treo. Lấy g ≈ 10 m/s2. Xác định động năng của hệ vật khi vật m1 đi xuống phía dưới được một đoạn 50 cm.
Phương pháp giải
- Vận dụng lí thuyết về định luật bảo toàn cơ năng và công thức tính trọng lượng vào quá trình chuyển động của vật
- Áp dụng công thức định luật bảo toàn cơ năng, tìm động năng của vật theo công thức:
\({{\rm{W}}_d} = \frac{1}{2}\left( {{m_1} + {m_2}} \right){v^2} = gh\left( {{m_1} - {m_2}\sin {{30}^0}} \right)\)
Hướng dẫn giải
- Hệ hai vật m1 và m2 chuyển động trong trọng trường, chỉ chịu tác dụng của trọng lực, nên cơ năng của hệ vật bảo toàn.
Vật m1, có trọng lượng P1 = m1g ≈ 20 N và vật m2 có trọng lượng P2 = m2g ≈ 1.10 = 10 N. Vì sợi dây nối hai vật này không dãn và P1 > P2, nên vật m1 chuyển động, thẳng đứng đi xuống và vật m2 bị kéo trượt lên phía đỉnh mặt nghiêng với cùng đoạn đường đi và vận tốc. Như vậy, khi vật m1 đi xuống một đoạn h thì thế năng của nó giảm một lượng Wt1 = m1gh, đồng thời vật m2 cũng trượt lên phía đỉnh mặt nghiêng một đoạn h nên độ cao của nó tăng thêm một lượng hsinα và thế năng cũng tăng một lượng Wt2 = m2gh.
- Theo định luật bảo toàn cơ năng, độ tăng động năng của hệ vật chuyển động trong trọng trường bằng độ giảm thế năng của hệ vật đó, tức là :
ΔWđ = - ΔWt
\(\frac{1}{2}\left( {{m_1} + {m_2}} \right){v^2} = {m_1}gh - {m_2}gh\sin \alpha \)
Suy ra :
\({{\rm{W}}_d} = \frac{1}{2}\left( {{m_1} + {m_2}} \right){v^2} = gh\left( {{m_1} - {m_2}\sin {{30}^0}} \right)\)
- Thay số, ta tìm được động năng của hệ vật khi vật m1 đi xuống phía dưới một đoạn h = 50 cm :
Wđ = 10.50.10-2.(2 - 1.0,5) = 7,5 J
10. Giải bài IV.10 trang 65 SBT Vật lý 10
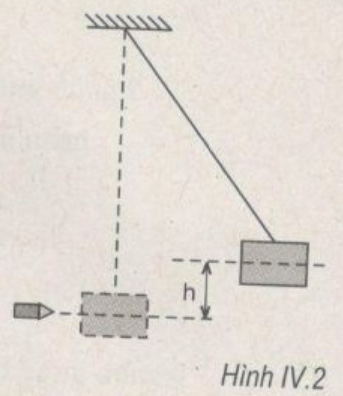
Một hộp đựng đầy cát khối lượng 2,5 kg được treo bằng sợi dây dài có đầu trên gắn với giá đỡ tại điểm O như hình IV.2. Khi bắn viên đạn theo phương ngang thì đầu đạn có khối lượng 20 g bay tới xuyên vào hộp cát, đẩy hộp cát chuyển động theo một cung tròn, làm cho trọng tâm của hộp cát nâng cao thêm 0,2 m so với vị trí cân bằng của nó. Bỏ qua lực cản, lực ma sát và khối lượng của dây treo. Xác định vận tốc của đầu đạn trước khi xuyên vào hộp cát. Lấy g = 9,8 m/s2.
Phương pháp giải
Vận dụng lí thuyết và công thức về định luật bảo toàn động lượng cho hệ vật:
(m + M)V = mv để tìm vận tốc của đầu đạn theo công thức:
\(v = \frac{{m + M}}{m}\sqrt {2gh} \)
Hướng dẫn giải
Hệ vật gồm "Đầu đạn - Hộp cát - Trái Đất" là một hệ cô lập, vì không có các ngoại lực (lực cản, lực ma sát) tác dụng. Do đó, động lượng và cơ năng của hệ vật bảo toàn. Chọn mặt đất làm gốc tính thế năng trọng trường và chiều chuyển động của các vật là chiều dương
- Áp dụng định luật bảo toàn động lượng cho quá trình va chạm mềm khi đầu đạn bay tới xuyên vào hộp cát theo phương ngang, ta có :
(m + M)V = mv => V = mv/(m+M)
trong đó v là vận tốc của đầu đạn có khối lượng m, còn V là vận tốc của hộp cát chứa đầu đạn có tổng khối lượng M + m.
- Áp dụng định luật bảo toàn cơ năng cho quá trình khi hộp cát chứa đầu đạn có vận tốc V chuyển động trong trọng trường và trọng tâm của nó được nâng cao thêm một đoạn h so với vị trí cân bằng, ta có :
\(\begin{array}{l} \left( {m + M} \right)gh = \frac{{\left( {m + M} \right){V^2}}}{2}\\ \Rightarrow V = \sqrt {2gh} \end{array}\)
Từ hai phương trình trên, ta suy ra vận tốc của đầu đạn :
\(\begin{array}{l} v = \frac{{m + M}}{m}\sqrt {2gh} \\ = \frac{{{{20.10}^{ - 3}} + 2,5}}{{{{20.10}^{ - 3}}}}.\sqrt {2.9,8.0,2} = 249,5(m/s) \end{array}\)
11. Giải bài IV.11 trang 65 SBT Vật lý 10
Một lò xo có độ cứng 500 N/m nằm ngang, một đầu gắn cố định, đầu còn lại gắn với một vật khối lượng 200 g. Cho vật trượt trên một mặt phẳng ngang không ma sát. Khi vật đi qua vị trí cân bằng (lò xo không biến dạng), vật có động năng bằng 3,6 J. Xác định :
a) Vận tốc của vật tại vị trí cân bằng.
b) Công suất của lực đàn hồi tại vị trí lò xo bị nén 10 cm và vật đang rời xa vị trí cân bằng.
Phương pháp giải
Áp dụng định luật bảo toàn cơ năng:
\({\rm{W}} = {{\rm{W}}_{dh}} + {{\rm{W}}_d} = \frac{{k{{\left( {{\rm{\Delta }}l} \right)}^2}}}{2} + \frac{{m{v^2}}}{2}\)
a) Tính vận tốc theo công thức:
\({v_O} = \sqrt {\frac{{2{W_d}\left( O \right)}}{m}} \)
b) Để tính công suất của lực đàn hồi, ta làm theo cách sau:
- Tính lực đàn hồi theo công thức:
Fdh = -k .Δl
- Tính cơ năng tại A:
\({\rm{W}}\left( A \right) = \frac{{mv_A^2}}{2} + \frac{{k{{\left( {{\rm{\Delta }}l} \right)}^2}}}{2}\)
- Áp dụng định luật bảo toàn cơ năng, tìm vận tốc theo công thức:
\({v_A} = \sqrt {v_O^2 - \frac{{k{{\left( {{\rm{\Delta }}l} \right)}^2}}}{m}} \)
- Áp dụng công thức: P = |FđhvA| để tính công suất của lực
Hướng dẫn giải
Hệ vật "Lò xo — Vật trượt -Trái Đất" là hệ cô lập (do không chịu ngoại lực tác dụng) nên cơ năng của hệ vật bảo toàn.
Chọn mặt phẳng ngang làm mốc thế năng trọng trường (Wt = 0) và chọn vị trí cân bằng của vật tại điểm O làm mốc thế năng đàn hồi (Wđh = 0). Vì hệ vật chuyển động trên cùng mặt phẳng ngang, nên cơ năng của hệ vật tại vị trí bất kì có giá trị bằng tổng của thế năng đàn hồi và động năng :
\({\rm{W}} = {{\rm{W}}_{dh}} + {{\rm{W}}_d} = \frac{{k{{\left( {{\rm{\Delta }}l} \right)}^2}}}{2} + \frac{{m{v^2}}}{2}\)
a) Khi hệ vật nằm cân bằng tại vị trí O: lò xo không biến dạng ( Δl = 0 ) nên thế năng đàn hồi Wđh (O) = 0 và cơ năng của hệ vật có giá trị đúng bằng động năng của vật trượt. Từ đó suy ra vận tốc của vật tại vị trí O :
\({v_O} = \sqrt {\frac{{2{W_d}\left( O \right)}}{m}} = \sqrt {\frac{{2.3,6}}{{0,2}}} = 6(m/s)\)
b) Muốn xác định công suất của lực đàn hồi, ta phải tính được lực đàn hồi của lò xo và vận tốc của vật tại cùng một vị trí.
Chọn chiểu lò xo bị nén là chiều dương. Tại vị trí A : lò xo bị nén một đoạn Δl = 10 cm > 0 và vật rời xa vị trí cân bằng có vận tốc v > 0, nên lực đàn hồi của lò xo (chống lại lực nén) ngược hướng với vận tốc của vật và có giá trị bằng :
Fdh = -k .Δl =-500. 10.10-2 = -50N < 0
- Cơ năng của hệ vật tại vị trí A bằng :
\({\rm{W}}\left( A \right) = \frac{{mv_A^2}}{2} + \frac{{k{{\left( {{\rm{\Delta }}l} \right)}^2}}}{2}\)
- Áp dụng định luật bảo toàn cơ năng cho hệ vật, ta có:
\({\rm{W}}\left( A \right) = {\rm{W}}\left( O \right) = > \frac{{mv_A^2}}{2} + \frac{{k{{\left( {{\rm{\Delta }}l} \right)}^2}}}{2} = \frac{{mv_O^2}}{2}\)
Hay: \({v_A} = \sqrt {v_O^2 - \frac{{k{{\left( {{\rm{\Delta }}l} \right)}^2}}}{m}} \)
- Thay số, ta tìm được vận tốc của vật trượt tại vị trí A :
\({v_A} = \sqrt {{6^2} - \frac{{500.{{\left( {{{10.10}^{ - 2}}} \right)}^2}}}{{{{200.10}^{ - 3}}}}} = 3(m/s)\)
- Từ đó suy ra công suất của lực đàn hồi tại vị trí A có độ lớn bằng :
P = |FđhvA| = 50.3 = 150 W
12. Giải bài IV.12 trang 65 SBT Vật lý 10
Một lò xo được đặt thẳng đứng, đầu dưới cố định, đầu trên đỡ một vật khối lượng 8 kg. Bỏ qua khối lượng của lò xo và lực cản của không khí.
a) Khi hệ vật nằm cân bằng tại vị trí O, lò xo bị nén một đoạn 10 cm. Xác định độ cứng của lò xo. Lấy g ≈ 10 m/s2.
b) Ấn vật xuống phía dưới tới vị trí A để lò xo bị nén thêm 30 cm, rồi buông nhẹ tay thả cho vật chuyển động. Xác định thế năng đàn hồi của lò xo tại vị trí A và độ cao lớn nhất mà vật đạt tới so với vị trí A.
Phương pháp giải
Áp dụng định luật bảo toàn cơ năng cho hệ vật:
\(\begin{array}{l} {\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} + {{\rm{W}}_{dh}}\\ = \frac{{m{v^2}}}{2} + mgh + \frac{{k{{\left( {{\rm{\Delta }}l} \right)}^2}}}{2} \end{array}\)
a) Tính độ cứng k theo công thức:
\(\begin{array}{l} k = \frac{{mg}}{{{\rm{\Delta }}{l_0}}} \end{array}\)
b) Để tính thế năng đàn hồi và độ cao lớn nhất mà vật đạt được ta làm như sau:
- Tính cơ năng tại A theo công thức:
\(\begin{array}{l} {\rm{W}}\left( A \right) = {{\rm{W}}_{dh}}\left( A \right) = \frac{{k{{\left( {{\rm{\Delta }}l} \right)}^2}}}{2}\\ \end{array}\)(đúng bằng thế năng đàn hồi)
- Tính cơ năng tại C theo công thức:
\(W\left( C \right) = mg\left( {{\rm{\Delta }}l + {h_{\max }}} \right) + \frac{{kh_{\max }^2}}{2}\)
- Áp dụng định luật bảo toàn cơ năng tại hai vị trí, ta được phương trình:
\(\begin{array}{l} 8.10.\left( {{{40.10}^{ - 2}} + {h_{\max }}} \right) + \frac{{800h_{\max }^2}}{2} = 64\\ \Rightarrow 50{h^2} + 10h - 4 = 0 \end{array}\)
⇒ Giải phương trình để tìm độ cao cực đại
Hướng dẫn giải
Hệ vật "lò xo - vật - Trái Đất" là hệ cô lập (do không chịu ngoại lực tác dụng) nên cơ năng của hệ vật bảo toàn.
Chọn mặt phẳng ngang đi qua vị trí A làm mốc tính thế năng trọng trường (Wt = 0) và chọn vị trí lò xo không bị biến dạng làm mốc thế năng đàn hồi (Wđh = 0). Khi đó cơ năng của hệ vật tại vị trí bất kì có giá trị bằng tổng của động năng Wđ thế năng trọng trường Wt và thế năng đàn hồi Wđh :
\(\begin{array}{l} {\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} + {{\rm{W}}_{dh}}\\ = \frac{{m{v^2}}}{2} + mgh + \frac{{k{{\left( {{\rm{\Delta }}l} \right)}^2}}}{2} \end{array}\)
a) Tại vị trí cân bằng O : hệ vật đứng yên, lò xo bị nén một đoạn Δl0 =10 cm và lực đàn hồi Fđh cân bằng với trọng lực P tác dụng lên vật :
\(\begin{array}{l} k{\rm{\Delta }}{l_0} = mg\\ \Rightarrow k = \frac{{mg}}{{{\rm{\Delta }}{l_0}}} = \frac{{8.10}}{{{{10.10}^{ - 2}}}} = 800(N/m) \end{array}\)
b) Tại vị trí A, lò xo bị nén một đoạn Δl = (10 + 30).10-2 = 40.10-2 m, vật có động năng Wđ(A) = 0 và thế năng trọng trường Wt(A) = 0, nên cơ năng của hệ vật tại A đúng bằng thế năng đàn hồi của lò xo :
\(\begin{array}{l} {\rm{W}}\left( A \right) = {{\rm{W}}_{dh}}\left( A \right) = \frac{{k{{\left( {{\rm{\Delta }}l} \right)}^2}}}{2}\\ = \frac{{800.{{\left( {{{40.10}^{ - 2}}} \right)}^2}}}{2} = 64\left( J \right) \end{array}\)
Khi buông nhẹ tay để thả cho vật từ vị trí A chuyển động lên phía trên tới vị trí B cách A một đoạn Δl = 40 cm, tại đó lò xo không bị biến dạng, thế năng đàn hồi Wđh = 0. Sau đó, vật tiếp tục chuyển động từ vị trí B lên tới vị trí C có độ cao hmax = BC, tại đó vật có vận tốc vC = 0 và động năng Wđ (C) = 0, nên cơ năng của hệ vật tại C bằng :
\(W\left( C \right) = mg\left( {{\rm{\Delta }}l + {h_{\max }}} \right) + \frac{{kh_{\max }^2}}{2}\)
- Áp dụng định luật bảo toàn cơ năng cho chuyển động của hệ vật từ vị trí A qua vị trí B tới vị trí C, ta có:
\(\begin{array}{l} W\left( C \right) = W\left( B \right) = W(A)\\ \Rightarrow mg\left( {{\rm{\Delta }}l + {h_{\max }}} \right) + \frac{{kh_{\max }^2}}{2} = 64 \end{array}\)
- Thay số, ta tìm được độ cao hmax = BC :
\(\begin{array}{l} 8.10.\left( {{{40.10}^{ - 2}} + {h_{\max }}} \right) + \frac{{800h_{\max }^2}}{2} = 64\\ \Rightarrow 50{h^2} + 10h - 4 = 0 \end{array}\)
- Phương trình này có nghiệm số dương : hmax = BC = 20 cm.
Như vậy, độ cao lớn nhất mà vật đạt tới so với vị trí A bằng :
Hmax = AB + BC = 40 + 20 = 60 cm