Giải bài tập SBT Vật Lí 10 Bài 34 - 35: Chất rắn kết tinh. Chất rắn vô định hình. Biến dạng cơ của vật rắn

Một thanh đồng có đường kính 20 mm. Xác định độ biến dạng nén tỉ đối của thanh này khi hai đầu của nó chịu tác dụng một lực nén bằng 94,2 kN. Cho biết suất đàn hồi của đồng là 11,8.10^l0 Pa.

A. 0,25%.            

B. 0,025%.          

C. 5,2%.              

D. 0,52%.

Phương pháp giải

- Áp dụng công thức: 

\(\begin{array}{l} S = \pi {r^2} = \frac{{\pi {d^2}}}{4}\\ \end{array}\)để tính diện tích tiếp xúc

- Độ biến dạng nén tỉ đối của thanh được tính theo công thức:

\(\begin{array}{l} \frac{{\left| {{\rm{\Delta }}\ell } \right|}}{{{\ell _0}}} = \frac{F}{{S.E}} \end{array}\)

Hướng dẫn giải

- Diện tích mặt tiếp xác là:

\(\begin{array}{l} S = \pi {r^2} = \frac{{\pi {d^2}}}{4}\\ = \frac{{\pi .{{(20:1000)}^2}}}{4} = {10^4}\pi ({m^2}) \end{array}\)

- Ta có:

\(\begin{array}{l} \sigma = \frac{F}{S} = E\frac{{\left| {{\rm{\Delta }}\ell } \right|}}{{{\ell _0}}}\\ \Rightarrow \frac{{\left| {{\rm{\Delta }}\ell } \right|}}{{{\ell _0}}} = \frac{F}{{S.E}} = \frac{{94200}}{{{{10}^{ - 4}}\pi {{.11,8.10}^{10}}}} = 0,25{\rm{\% }} \end{array}\)

- Chọn đáp án A

Một dây cáp của cần cẩu chỉ chịu được ứng suất kéo không quá 60.10⁶ Pa. Hỏi dây cáp này phải có đường kính nhỏ nhất bằng bao nhiêu để nó có thể kéo một vật trọng lượng 25 kN.

A. 23 cm.            

B. 2,3 mm.            

C. 23 mm.          

D. 3,2 cm.

Phương pháp giải

- Tính diện tích nhỏ nhất theo công thức:

\( {S_{\min }} = \frac{F}{{{\sigma _{\max }}}} \)

- Áp dụng công thức:

\({d_{\min }} = \sqrt {\frac{{4S}}{\pi }} \) để tinh đường kính nhỏ nhất

Hướng dẫn giải

- Ta có:

\({\sigma _{\max }} = {60.10^6}Pa;F = 25kN = 25000N\)

- Diện tích tiếp xúc tối thiểu là:

\(\begin{array}{l} \sigma = \frac{F}{S}\\ \Rightarrow {S_{\min }} = \frac{F}{{{\sigma _{\max }}}} = \frac{{25000}}{{{{60.10}^6}}} = \frac{1}{{2400}}({m^2}) \end{array}\)

Mà:

\(\begin{array}{l} S = \frac{{\pi {d^2}}}{4}\\ \Rightarrow {d_{\min }} = \sqrt {\frac{{4S}}{\pi }} = \sqrt {\frac{4}{{2400.\pi }}} = 0,023m = 23mm \end{array}\)

- Chọn đáp án C

Một thanh thép dài 5 m có tiết diện 1,5 cm² được giữ chặt một đầu. Khi chịu lực kéo tác dụng, thanh thép bị dãn dài thêm 2,5 mm. Cho biết suất đàn hồi của thép là E = 2,16.10¹¹ Pa. Hãy xác định độ lớn của lực kéo này.

A. F = 6.10⁴N.                      

B. F = 1,62.10⁴N.

C.F= 1,5.10⁷ N.                    

D. F = 3,5.10⁵ N.

Phương pháp giải

Áp dụng công thức: 

\(F = \frac{{E.{\rm{\Delta }}\ell .S}}{{{\ell _0}}}\) để tính lực kéo

Hướng dẫn giải

- Ta có:

\(\begin{array}{l} \sigma = \frac{F}{S} = E\frac{{{\rm{\Delta }}\ell }}{{{\ell _0}}}\\ \Rightarrow F = \frac{{E.{\rm{\Delta }}\ell .S}}{{{\ell _0}}} = \frac{{{{2,16.10}^{11}}{{.2,5.10}^{ - 3}}{{.1,5.10}^{ - 4}}}}{5} = 16200N = {1,62.10^4}N \end{array}\)

- Chọn đáp án B

Một sợi dây sắt dài gấp đôi nhưng có tiết diện nhỏ bằng nửa tiết diện của sợi dây đồng. Giữ chặt đầu trên của mỗi sợi dây này và treo vào đầu dưới của mỗi dây một vật nặng giống nhau. Cho biết suất đàn hồi của sắt lớn hơn của đồng 1,6 lần. Hỏi sợi dây sắt bị dãn nhiều hơn hay ít hơn bao nhiêu lần so với sợi dây đồng ?

A. Dây sắt dãn ít hơn 1,6 lần.          B. Dây sắt dãn nhiều hơn 1,6 lần.

C. Dây sắt dãn ít hơn 2,5 lần.          D. Dây sắt dãn nhiều hơn 2,5 lần.

Phương pháp giải

- Từ công thức tính ứng suất tính độ tăng chiều dài theo công thức:

\({\rm{\Delta }}{l_1} = \frac{{F.{l_{01}}}}{{{S_1}.{E_1}}};{\rm{\Delta }}{l_2} = \frac{{F.{l_{02}}}}{{{S_2}.{E_2}}}\)

- Lập tỉ số hai giá trị trên:

\(\frac{{{\rm{\Delta }}{l_1}}}{{{\rm{\Delta }}{l_2}}} = \frac{{{l_{01}}}}{{{l_{02}}}}\frac{{{S_2}}}{{{S_1}}}\frac{{{E_2}}}{{{E_1}}}\) để tìm độ tăng chiều dài

Hướng dẫn giải

\({l_{01}} = 2{l_{02}};{S_1} = \frac{1}{2}{S_2};{E_1} = 1,6{E_2}\)

- Ta có:

\(\sigma = \frac{F}{S} = E\frac{{{\rm{\Delta }}l}}{{{l_0}}}\)

- Tỉ lệ về độ tăng chiều dài là:

\(\begin{array}{l} {\rm{\Delta }}{l_1} = \frac{{F.{l_{01}}}}{{{S_1}.{E_1}}};{\rm{\Delta }}{l_2} = \frac{{F.{l_{02}}}}{{{S_2}.{E_2}}}\\ \Rightarrow \frac{{{\rm{\Delta }}{l_1}}}{{{\rm{\Delta }}{l_2}}} = \frac{{F.{l_{01}}}}{{{S_1}.{E_1}}}\frac{{{S_2}.{E_2}}}{{F.{l_{02}}}} = \frac{{{l_{01}}}}{{{l_{02}}}}\frac{{{S_2}}}{{{S_1}}}\frac{{{E_2}}}{{{E_1}}}\\ = 2.2.\frac{1}{{1,6}} = 2,5 \end{array}\)

- Chọn đáp án D

Khi đun nóng chảy thiếc, đặc điểm gì chứng tỏ thiếc không phải là chất rắn vô định hình mà là chất rắn kết tinh?

Phương pháp giải

Chất rắn kết tinh có nhiệt độ nóng chảy xác định

Hướng dẫn giải

Quan sát thấy thiếc nóng chảy ở nhiệt độ xác định không đổi. Đặc điểm này chứng tỏ thiếc không phải là vật rắn vô định hình, mà là chất rắn kết tinh.

Sắt, đồng, nhôm và các kim loại khác dùng trong thực tế đều là những chất rắn kết tinh. Tại sao người ta không phát hiện được tính dị hướng của các chất rắn này ?

Phương pháp giải

Chất rắn kết tinh có tính đẳng hướng

Hướng dẫn giải

Sắt, đồng, nhôm và các kim loại khác dùng trong thực tế thường là các vật rắn đa tinh thể. Chất rắn đa tinh thể cấu tạo từ vô số các tinh thể nhỏ sắp xếp hỗn độn nên tính dị hướng của các tinh thể nhỏ được bù trừ trong toàn khối chất vì thế không phát hiện được tính dị hướng trong khối kim loại.

Thanh dầm ngang bằng bê tông cốt thép luôn chịu tác dụng lực có xu  hướng làm thanh dầm bị uốn cong. Cho biết bê tông chịu nén tốt, nhưng chịu kéo dãn kém. Hỏi trong phần nào của thanh dầm này, các thanh thép dùng làm cốt phải có đường kính lớn hơn và được đặt mau (dày) hơn ?

Phương pháp giải

Để trả lời câu hỏi này cần nắm được đặc điểm về sự biến dạng của vật rắn về mặt cơ học

Hướng dẫn giải

Khi thanh dầm ngang bằng bê tông cốt thép chịu biến dạng uốn thì phần nửa phía dưới chịu biến dạng kéo dãn và phần nửa phía trên chịu biến dạng nén. Vì bê tông chịu nén tốt, nhưng chịu kéo dãn kém nên cần phải dùng các thanh thép làm cốt có đường kính lớn hơn và phải đặt chúng mau (dày) hơn trong phần nửa phía dưới của thanh dầm bê tông.

Một thanh xà ngang bằng thép dài 5 m có tiết diện 25 cm². Hai đầu của thanh xà được gắn chặt vào hai bức tường đối diện. Hãy tính áp lực do thanh xà tác dụng lên hai bức tường khi thanh xà dãn dài thêm 1,2 mm do nhiệt độ của nó tăng. Cho biết thép có suất đàn hồi E = 20.10¹⁰ Pa. Bỏ qua biến dạng của các bức tường.

Phương pháp giải

Tính áp lực do thanh xà tác dụng lên hai bức tường theo công thức:

\(F = E\frac{S}{{{l_0}}}{\rm{\Delta }}l\)

Hướng dẫn giải

Vì hai bức tường cố định nên khoảng cách giữa chúng không đổi. Khi nhiệt độ tăng thì thanh xà nở dài thêm một đoạn Δl = 1,2 mm. Do đó, thanh xà tác dụng lên hai bức tường một lực có cường độ tính theo định luật Húc:

\(\begin{array}{l} F = E\frac{S}{{{l_0}}}{\rm{\Delta }}l\\ = {20.10^{10}}\frac{{{{25.10}^{ - 4}}}}{5}{.1,2.10^{ - 3}} = {1,6.10^5}\left( N \right) \end{array}\)

Một chiếc cột bê tông cốt thép chịu lực nén F thẳng đứng do tải trọng đè lên nó. Giả sử suất đàn hồi của bê tông bằng 1/10 của thép, còn diện tích tiết diện  ngang của thép bằng khoảng 1/20 của bê tông. Hãy tính phần lực nén do tải trọng tác dụng lên phần bê tông của chiếc cột này.

Phương pháp giải

- Áp dụng công thức:

\({F} = {E}\frac{{{S}}}{l}{\rm{\Delta }}\) để tính lực nén do tải trọng tác dụng lên phần bê tông và do tải trọng tác dụng lên phần cốt thép

- Lập tỉ số giữa hai lực nén trên:

\(\frac{{{F_1}}}{{{F_2}}} = \frac{{{E_1}{S_1}}}{{{E_2}{S_2}}} = 2\)

- Tính lực nén bê tông theo công thức: F₁ = 2/3 F

Hướng dẫn giải

Gọi F₁ là phần lực nén do tải trọng tác dụng lên phần bê tông của chiếc cột và F₂ là phần lực nén do tải trọng tác dụng lên phần cốt thép của chiếc cột. Áp dụng định luật Húc, ta có :

\({F_1} = {E_1}\frac{{{S_1}}}{l}{\rm{\Delta }}l\,\,và\,\,{F_2} = {E_2}\frac{{{S_2}}}{l}{\rm{\Delta }}l\)

- So sánh F₁ với F₂ , với chú ý E₁/E₂ = 1/10 và S₂/S₁ = 1/20, ta tìm được

\(\frac{{{F_1}}}{{{F_2}}} = \frac{{{E_1}{S_1}}}{{{E_2}{S_2}}} = 2\)

- Vì F₁ + F₂ = F, nên ta suy ra : F₁ = 2/3 F

Như vậy, lực nén lên bê tông bằng 2/3 lực nén của tải trọng tác dụng lên cột.

Người ta dùng một thanh sắt tròn có độ dài ban đầu l₀= 50 cm và tiết diện ngang S = 2,5 mm². Kéo dãn thanh sắt bằng lực F có cường độ tăng dần và đo độ dãn dài Δl tương ứng của nó (Bảng 34-35.1).

a) Tính độ dãn dài tỉ đối ε của thanh sắt và ứng suất σ của lực kéo tác dụng lên nó trong mỗi lần đo (Bảng 34-35. 1).

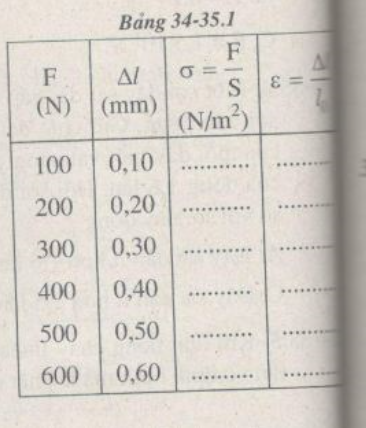
b) Vẽ đồ thị biểu diễn sự phụ thuộc của ε vào σ.

c) Dựa vào đồ thị vẽ được, tìm giá trị của suất đàn hồi E và hệ số đàn hồi k.

Phương pháp giải

a) Tính độ dãn dài tỉ đối ε và ứng suất σ theo bảng bên dưới

b) Vẽ đồ thị như như hình bên dưới với: \(\begin{array}{l} \tan \theta = \frac{{MH}}{{AH}}\\ \end{array}\)

c) Suất đàn hồi E và hệ số đàn hồi k được tính theo công thức:

\(E = \frac{1}{{\tan \theta }}\) và \(k = E\frac{S}{{{l_0}}}\)

Hướng dẫn giải

a) Tính độ dãn dài tỉ đối ε của thanh sắt và ứng suất σ của lực kéo tác dụng lên thanh sắt trong mỗi lần đo.

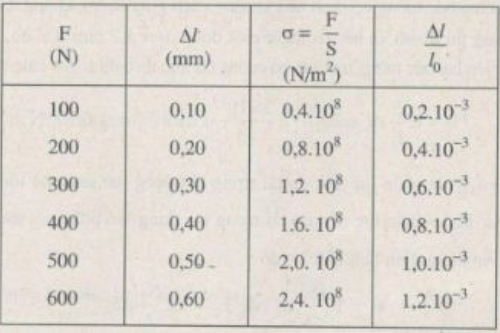
b) Vẽ đồ thị biểu diễn sự phụ thuộc của ε vào σ.

Chọn tỉ lệ vẽ trên các trục tọa độ:

- Trục hoành: 1 cm → σ = 0,5.108 N/m².

- Trục tung: 1 cm → ε = 0,2.10^-3.

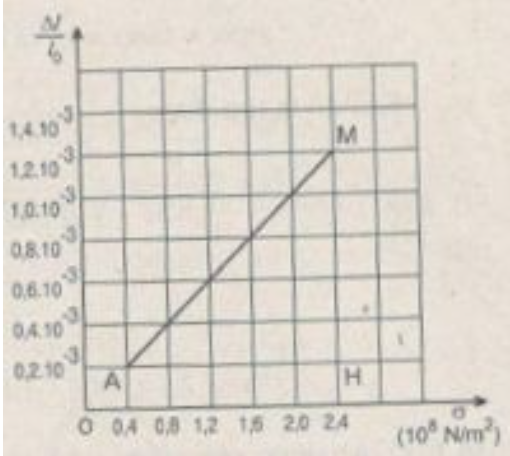
Đồ thị có dạng đường thẳng chứng tỏ độ biến dạng tỉ đối Δl/l₀ của thanh sắt tỉ lệ thuận với ứng suất σ của lực kéo tác dụng lên thanh sắt, nghĩa là:

\(\varepsilon = \frac{{{\rm{\Delta }}l}}{{{l_0}}} = a\varepsilon \)

Hệ số tỉ lệ a được xác định bởi hệ số góc của đường biểu diễn đồ thị:

\(\begin{array}{l} \tan \theta = \frac{{MH}}{{AH}}\\ = \frac{{{{1,2.10}^{ - 3}} - {{0,2.10}^{ - 3}}}}{{{{2,4.10}^8} - {{0,4.10}^8}}} = {0,5.10^{ - 11}} \end{array}\)

c) Tìm giá trị của suất đàn hồi E và hệ số đàn hồi k của thanh sắt.

Theo định luật Húc: \(F = k\left| {{\rm{\Delta }}l} \right| = E\frac{S}{{{l_0}}}{\rm{\Delta }}l\)

ta suy ra: \(\frac{{{\rm{\Delta }}l}}{{{l_0}}} = \frac{1}{E}.\frac{F}{S}\)

Từ đó tìm đươc suất đàn hồi :

\(E = \frac{1}{{\tan \theta }} = \frac{1}{{{{0,5.10}^{ - 11}}}} = {20.10^{10}}Pa\)

và hệ số đàn hồi:

\(k = E\frac{S}{{{l_0}}} = {20.10^{10}}.\frac{{{{2,5.10}^{ - 6}}}}{{{{50.10}^{ - 2}}}} = {1.10^6}N/m\)