Giải bài tập SBT Vật Lí 10 Bài 15: Bài toán về chuyển động ném ngang

Bi A có trọng lượng lớn gấp đôi bi B. Cùng một lúc tại một mái nhà ở cùng độ cao, bi A được thả rơi còn bi B được ném theo phương ngang với tốc độ lớn. bỏ qua sức cản của không khí.

Hãy cho biết câu nào dưới đây là đúng.

A. A chạm đất trước B.

B. A chạm đất sau B.

C. Cả hai đều chạm đất cùng một lúc

D. Chưa đủ thông tin để trả lời 

Phương pháp giải

Thời gian rơi tự do không phụ thuộc trọng lượng vật, do đó các vật chạm đất cùng lúc

Hướng dẫn giải

- Cả hai đều chạm đất cùng một lúc

- Chọn đáp án C

Một viên bi X được ném ngang từ một điểm. Cùng lúc đó, tại cùng độ cao, một viên bi Y có cùng kích thước nhưng có khối lượng gấp đôi được thả rơi từ trạng thái nghỉ. Bỏ qua sức cản của không khí. Hỏi điều gì sau đây sẽ xảy ra?

A. Y chạm sàn trước X.

B. X chạm sàn trước Y.

C. Y chạm sàn trong khi X mới đi được nửa đường.

D. X và Y chạm sàn cùng một lúc. 

Phương pháp giải

Thời gian rơi tự do không phụ thuộc khối lượng vật, do đó các vật chạm đất cùng lúc

Hướng dẫn giải

- X và Y chạm sàn cùng một lúc. 

- Chọn đáp án D

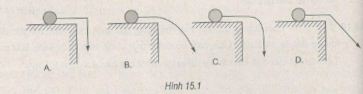
Một quả bóng tennit được đặt trên mặt bàn và được truyền một vận tốc đầu theo phương ngang. Hình nào miêu tả quỹ đạo của quả bóng khi rơi ra khỏi bàn ?

Phương pháp giải

Vận dụng lí thuyết về chuyển động ném ngang của vật để trả lời câu hỏi này

Hướng dẫn giải

Hình B miêu tả quỹ đạo của quả bóng khi rơi ra khỏi bàn

Tại cùng một độ cao so với mặt đất và cùng một lúc, vật A được thả rơi tự do còn vật B được ném ngang. Hỏi câu nói nào sau đây là đúng ?

A. Hai vật chạm đất cùng lúc và có tốc độ lúc chạm đất bằng nhau.

B. Vật A chạm đất trước và có tốc độ lúc chạm đất nhỏ hơn.

C. Vật B chạm đất trước và có tốc độ lúc sắp chạm đất lớn hơn.

D. Hai vật chạm đất cùng lúc và vật B có tốc độ lúc chạm đất lớn hơn. 

Phương pháp giải

Vật bị ném sẽ có vật tốc lớn hơn vật thả rơi tự do nếu xét cùng một độ cao

Hướng dẫn giải

- Hai vật chạm đất cùng lúc và vật B có tốc độ lúc chạm đất lớn hơn. 

- Chọn đáp án D

Khi nói về chuyển động nệm ngang, câu nói nào dưới đây là sai ?

A. Trong chuyển động ném ngang, vectơ vận tốc của vật luôn luôn thay đổi phương.

B. Trong chuyển động ném ngang, độ lớn của vectơ vận tốc của vật tăng dần.

C. Gia tốc của chuyển động ném ngang là gia tốc rơi tự do.

D. Từ cùng một độ cao trên mặt đất ta có thể tăng tốc độ ban đầu của vật ném ngang để vật rơi xuống đất nhanh hơn. 

Phương pháp giải

Các vật rơi tự do trong cùng thời gian bằng nhau nếu xét cùng một độ cao, chúng chỉ khác nhau về vận tốc do tính chất của chuyển động

Hướng dẫn giải

- Từ cùng một độ cao trên mặt đất ta có thể tăng tốc độ ban đầu của vật ném ngang để vật rơi xuống đất nhanh hơn.→ D sai

- Chọn đáp án D

Một vật được ném theo phương ngang với vận tốc đầu v₀ = 30 m/s từ một độ cao h = 80 m so với mặt đất. Lấy g = 10 m/s². Bỏ qua sức cản của không khí. Thời gian rơi và tầm bay xa của vật là

A. 4 s ; 120 m.     B. 8 s ; 240 m.  

C. 2,8 s ; 84 m.    D. 2 s ; 60 m. 

Phương pháp giải

- Tính thời gian rơi theo công thức:

\(\begin{array}{l} t = \sqrt {\frac{{2h}}{g}} \end{array}\)

- Áp dụng công thức:

\(L = {v_0}\sqrt {\frac{{2h}}{g}} \) để tính tầm xa của vật

Hướng dẫn giải

- Thời gian rơi của vật là:

\(\begin{array}{*{20}{l}} {t = \sqrt {\frac{{2h}}{g}} } \end{array} = \sqrt {\frac{{2.80}}{{10}}} = 4s\)

- Tầm xa của vật là:

\(L = {v_0}\sqrt {\frac{{2h}}{g}} = 30.\sqrt {\frac{{2.80}}{{10}}} = 120m\)

Chọn đáp án A

Trong môn trượt tuyết, một vận động viên sau khi trượt trên đoạn đường dốc thì trượt ra khỏi dốc theo phương ngang ở độ cao 90 m so với mặt đất. Người đó bay xa được 180 m trước khi chạm đất. Hỏi tốc độ của vận động viên đó khi rời khỏi dốc là bao nhiêu ? Lấy g = 9,8 m/s². 

Phương pháp giải

- Tính thời gian rơi theo công thức:

\(\begin{array}{l} t = \sqrt {\frac{{2h}}{g}} \end{array}\)

- Áp dụng công thức:

\(\begin{array}{l} {v_0} = \frac{{{L_{\max }}}}{t} \end{array}\) để tính vận tốc ban đầu

Hướng dẫn giải

- Thời gian chuyển động của vận động viên là:

\(\begin{array}{l} h = \frac{1}{2}g{t^2}\\ = > t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.90}}{{9,8}}} = 4,2(s) \end{array}\)

- Vận tốc ban đầu là:

\(\begin{array}{l} {L_{\max }} = {v_0}t\\ = > {v_0} = \frac{{{L_{\max }}}}{t} = 42(m/s) \end{array}\)

Một người đứng ở một vách đá nhô ra biển và ném một hòn đá theo phương ngang xuống biển với tốc độ 18 m/s. Vách đá cao 50 m so với mặt nước biển. Lấy g = 9,8 m/s².

a) Sau bao lâu thì hòn đá chạm vào mặt nước ?

b) Tính tốc độ của hòn đá lúc chạm vào mặt nước. 

Phương pháp giải

a) Tính thời gian chạm vào nước theo công thức:

\(\begin{array}{l} t = \sqrt {\frac{{2h}}{g}} \end{array}\)

b) Áp dụng công thức:

\(v = \sqrt {v_x^2 + v_y^2} = \sqrt {v_0^2 + {{(gt)}^2}} \) để tính vận tốc 

Hướng dẫn giải

a)  Thời gian chạm vào nước là:

\(\begin{array}{l} y = h = \frac{1}{2}g{t^2}\\ = > t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.50,0}}{{9,8}}} = 3,19 \approx 3,2(s) \end{array}\)

b. Tính tốc độ của hòn đá lúc chạm vào mặt nước là:

\(v = \sqrt {v_x^2 + v_y^2} = \sqrt {v_0^2 + {{(gt)}^2}} = \sqrt {{{(18,0)}^2} + {{(9,8.3,19)}^2}} \)

= 36,06 ≈ 36 m/s

Một máy bay đang bay ngang với tốc độ 150 m/s ở độ cao 490 m thì thả một gói hàng. Lấy g = 9,8 m/s².

a) Bao lâu sau thì gói hàng sẽ rơi đến đất ?

b) Tầm bay xa (tính theo phương ngang) của gói hàng là bao nhiêu ?

c) Gói hàng bay theo quỹ đạo nào ? 

Phương pháp giải

a) Tính thời gian theo công thức:

\(\begin{array}{l} t = \sqrt {\frac{{2h}}{g}} \end{array}\)

b) Áp dụng công thức: L_max = v₀t để tính tầm xa

c) Quỹ đạo chuyển động ném ngang là đường parabol

Hướng dẫn giải

a. Thời gian gói hàng rơi đến đất là:

 \(t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.490}}{{9,8}}} = 10(s)\)

b. Gọi v₀ là tốc độ của gói hàng khi rời khỏi máy bay. Ta có:

L_max = v₀t = 150.10 = 1500 m.

c. Gói hàng bay theo quỹ đạo parabol.

Một vật được ném lên thẳng đứng sau 2 s lại rơi xuống đến vị trí ban đầu. Lấy g = 9,8 m/s². Tính:

a) Tốc độ ban đầu v₀ của vật.

b)  Độ cao h mà vật đạt tới. 

Phương pháp giải

a) Thay giá trị t vào phương trình sau để tính tốc độ:

\(\begin{array}{l} y = {v_0}t - \frac{1}{2}g{t^2} = 0\end{array}\)

b) Áp dụng công thức:

\({y_{\max }} = h = \frac{{v_0^2}}{{2g}}\) để tính độ cao cực đại

Hướng dẫn giải

a) Chuyển động ném lên thẳng đứng là chuyển động thẳng biến đổi đều với gia tốc là – g (chọn chiều dương hướng lên).

\(\begin{array}{l} y = {v_0}t - \frac{1}{2}g{t^2} = 0\\ = > t = \frac{{2{v_0}}}{g} = 2s\\ = > {v_0} = 9,8(m/s) \end{array}\)

b) Độ cao h mà vật đạt tới là:

 \({y_{\max }} = h = \frac{{v_0^2}}{{2g}} = {\frac{{(9,8)}}{{2.9,8}}^2} = 4,9(m)\)