Giải bài tập SGK Toán 12 Bài 2: Cực trị của hàm số

Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số sau

a) \(y = 2x^3 + 3x^2 - 36x - 10\)

b) \(y = x^4+ 2x^2 - 3\)

c) \(y = x + \frac{1}{x}\)

d) \(y = x^3(1 - x)^2\)

e) \(y = \sqrt {x^2-x+1}\)

Phương pháp giải

Để giải bài 1 các em cần ôn lại các bước tìm cực trị bằng quy tắc 1

• Bước 1: Tìm tập xác định của hàm số
• Bước 2: Tính \(f'(x)\). Tìm các điểm tại đó\(f'(x)=0\) hoặc \(f'(x)\) không xác định
• Bước 3: Lập bảng biến thiên
• Bước 4: Từ bảng biến thiên suy ra các điểm cực trị

Hướng dẫn giải

Câu a: Áp dụng quy tắc I, tìm các điểm cực trị của hàm số \(y = 2x^3 + 3x^2 - 36x - 10\)

Xét hàm số \(y = 2x^3 + 3x^2 - 36x - 10\)

Tập xác định: \(D=\mathbb{R}\)

Ta có đạo hàm: \(y' = 6{x^2} + 6x - 36\)

\(y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = 2\\ x = - 3 \end{array} \right.\)

Với x=2 ta có y=-54

Với x=-3 ta có y=71

Bảng biến thiên

Hàm số đạt cực đại tại x=-3, giá trị cực đại ycđ = y(-3) = 71

Hàm số đạt cực tiểu tại x = 2 , giá trị cực tiểu yct=y(2) =- 54

Câu b: Áp dụng quy tắc I, tìm các điểm cực trị của hàm số \(y = x^4+ 2x^2 - 3\)

Xét hàm số \(y = x^4+ 2x^2 - 3\)

Tập xác định: \(D=\mathbb{R}\)

Đạo hàm: \(y' = 4{x^3} + 4x = 4x({x^2} + 1)\)

\(y' = 0 \Leftrightarrow x = 0\)

Với x=0 ta có y=-3

Bảng biến thiên của hàm số

Hàm số đạt cực tiểu tại x=0, giá trị cực tiểu yct=y(0)=- 3

Hàm số không có cực đại

Câu c: Áp dụng quy tắc I, tìm các điểm cực trị của hàm số \(y = x + \frac{1}{x}\)

Xét hàm số \(y = x + \frac{1}{x}\)

Tập xác định: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)

\(y'=1-\frac{1}{x^2}=\frac{x^2-1}{x^2}=\frac{(x-1)(x+1)}{x^2}\)

\(y' = 0 \Leftrightarrow (x - 1)(x + 1) = 0 \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = 1 \end{array} \right.\)

Với x=1 ta có y=2

Với x=-1 ta có y=-2

Bảng biến thiên

Hàm số đạt cực đại tại x=-1, giá trị cực đại ycđ = y(-1) = -2

Hàm số đạt cực tiểu tại x = 1, giá trị cực tiểu yct = y(1) = 2

Câu d: Áp dụng quy tắc I, tìm các điểm cực trị của hàm số \(y = x^3(1 - x)^2\)

Xét hàm số \(y = x^3(1 - x)^2\)

Tập xác định: \(D=\mathbb{R}\)

Đạo hàm: \(y' = 3{x^2}{(1 - x)^2} - 2{x^3}(1 - x) \)

\(= {x^2}(1 - x)(3 - 5x)\)

\(y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = 1\\ x = \frac{3}{5}\\ x = 0 \end{array} \right.\)

Với \(x=1\) ta có \(y=0.\)

Với \(x=\frac{3}{5}\) ta có \(y=\frac{108}{3125}.\)

Với x=0 ta có \(y=0.\)

Bảng biến thiên

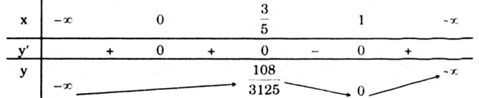
Hàm số đạt cực đại tại \(x=\frac{3}{5},\) giá trị cực đại \(y_{cd} =y\left ( \frac{3}{5} \right )=\frac{108}{3125}.\)

Hàm số đạt cực tiểu tại \(x=1,\) giá trị cực tiểu \(y_{ct}=y(1)=0.\)

Câu e: Áp dụng quy tắc I, tìm các điểm cực trị của hàm số \(y = \sqrt {x^2-x+1}\)

Xét hàm số \(y = \sqrt {x^2-x+1}\)

Tập xác định: \(D=\mathbb{R}\)

Đạo hàm: \({y' = \frac{{2x - 1}}{{2\sqrt {{x^2} - x + 1} }}}\)

\({y' = 0 \Leftrightarrow 2x - 1 = 0 \Leftrightarrow x = \frac{1}{2}}\)

Với \(x=\frac{1}{2}\) ta có \(y=\frac{\sqrt 3}{2}\).

Bảng biến thiên

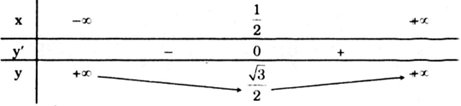
Vậy hàm số đạt cực tiểu tại \(x=\frac{1}{2}\), giá trị cực tiểu \(y_{ct}=y\left ( \frac{1}{2} \right )=\frac{\sqrt 3}{2}.\)

2. Giải bài 2 trang 18 SGK Giải tích 12

a) \(y = x^4 - 2x^2 + 1\)

b) \(y=\sin {2x} - x\)

c) \(y = sinx + cosx\)

d) \(y = x^5 - x^3 - 2x + 1\)

Phương pháp giải

Với những hàm số dễ dàng xét dấu của đạo hàm để lập bảng biến thiên ta thường dùng quy tắc I. Tuy nhiên trong quá trình tìm cực trị của hàm số các em sẽ gặp những hàm số mà việc xác định dấu của đạo hàm rất phức tạp thì chúng ta sẽ ưu tiên sử dụng quy tắc II để tìm cực trị. 

Trước khi giải bài 2, các em cần nắm được các bước đề tìm cực trị bằng quy tắc 2

• Bước 1: Tìm tập xác định của hàm số
• Bước 2: Tính f'(x). Tìm các nghiệm x_i của phương trình f'(x)=0
• Bước 3: Tính f''(x) và f''(x_i) suy ra tính chất cực trị của các điểm x_i

Chú ý: nếu f''(x_i)=0 thì ta phải dùng quy tắc 1 để xét cực trị tại x_i

Hướng dẫn giải

Câu a: Áp dụng quy tắc II, tìm các điểm cực trị của hàm số \(y = x^4 - 2x^2 + 1\)

Xét hàm số \(y = x^4 - 2x^2 + 1\)

Tập xác định \(D=\mathbb{R}\)

Đạo hàm:

\(\begin{array}{l} y' = 4{x^3} - 4x = 4x({x^2} - 1)\\ y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = - 1\\ x = 1 \end{array} \right. \end{array}\)

\(y'' = 12{x^2} - 4\)

Ta có

+ Với x = 0: \(y''(0) = -4 < 0\) nên hàm số đạt cực đại tại x=0, giá trị cực đại yCĐ = y(0) = 1

+ Với x = -1 và x = 1

\(y''(-1)=y''(1)=8>0\) nên hàm số đạt cực tiểu tại \(x= \pm1\), giá trị cực tiểu 

\(y_{CT}=y(-1)=y(1)=0.\)

Câu b: Áp dụng quy tắc II, tìm các điểm cực trị của hàm số \(y=\sin {2x} - x\)

Xét hàm số \(y = sin2x – x\)

Tập xác định \(D=\mathbb{R}\)

\(y' = 2cos2x - 1\).
\(y'=0\Leftrightarrow cos2x=\frac{1}{2}\Leftrightarrow 2x=\pm \frac{\pi }{3}+k2\pi \Leftrightarrow x=\pm \frac{\pi }{6}+k\pi , k \in \mathbb{Z}.\)

Đạo hàm cấp hai: \(y'' = -4sin2x .\)

Ta có

- Với \(x=\frac{\pi}{6}+k \pi\)

\(y''\left( {\frac{\pi }{6} + k\pi } \right) =  - 4\sin \left( {\frac{\pi }{3} + k2\pi } \right) \)

\(=  - 2\sqrt 3  < 0\)

Nên hàm số đạt cực đại tại các điểm \(x=\frac{\pi}{6}+k \pi\).

Giá trị cực đại

\({y_{CD}} = \sin \left( {\frac{\pi }{3} + k2\pi } \right) - \frac{\pi }{6} - k\pi \)

\(= \frac{{\sqrt 3 }}{2} - \frac{\pi }{6} - k\pi ,k \in \mathbb{Z}.\)

- Với \(x=-\frac{\pi}{6}+k \pi\)

\(y''\left( { - \frac{\pi }{6} + k\pi } \right) =  - 4\sin \left( { - \frac{\pi }{3} + k2\pi } \right)\)

\(= 2\sqrt 3  > 0\) 

Nên hàm số đạt cực tiểu tại các điểm \(x=-\frac{\pi}{6}+k \pi\).

Giá trị cực tiểu

\({y_{ct}} = \sin \left( { - \frac{\pi }{3} + k2\pi } \right) + \frac{\pi }{6} - k\pi \)

\(= - \frac{{\sqrt 3 }}{2} + \frac{\pi }{6} - k\pi ,k \in\mathbb{Z}\)

Câu c: Áp dụng quy tắc II, tìm các điểm cực trị của hàm số \(y = sinx + cosx\)

Xét hàm số \(y = sinx + cosx\)

Tập xác định \(D=\mathbb{R}\)

Đạo hàm: \(y' = \cos x - \sin x\)

\(\begin{array}{l} y' = 0 \Leftrightarrow \sin x = \cos x\\ \Leftrightarrow \tan x = 1 \Leftrightarrow x = \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}. \end{array}\)

Đạo hàm cấp 2: \(y''=-sinx-cosx.\)

- Với \(k=2m \left ( m \in \mathbb{Z} \right )\) ta có

\(y''\left( {\frac{\pi }{4} + 2m\pi } \right) = - \sin \frac{\pi }{4} - \cos \frac{\pi }{4}\)

\(= - \sqrt 2 < 0\)

Vậy hàm số đạt cực đại tại các điểm 

\(x = \frac{\pi }{4} + 2m\pi ,m \in \mathbb{Z}\)

- Với \(k=2m+1 \left ( m \in \mathbb{Z} \right )\) ta có

\(y''\left( {\frac{\pi }{4} + \left( {2m + 1} \right)\pi } \right) = \sin \frac{\pi }{4} + \cos \frac{\pi }{4}\)

\(= \sqrt 2 > 0.\)

Vậy hàm số đạt cực tiểu tại các điểm 

\(x = \frac{\pi }{4} + \left( {2m + 1} \right)\pi ,m \in \mathbb{Z}\)

Câu d: Áp dụng quy tắc II, tìm các điểm cực trị của hàm số \(y = x^5 - x^3 - 2x + 1\)

Xét hàm số \(y = x^5 - x^3 - 2x + 1\)

Tập xác định \(D=\mathbb{R}\)

Đạo hàm: \(y' = 5{x^4} - 3{x^2} - 2\)

\(y' = 0 \Leftrightarrow 5{x^4} - 3{x^2} - 2 = 0 \)

\(\Leftrightarrow {x^2} = 1 \Leftrightarrow x = \pm 1\)

(Đặt \(t=x^2>0\), giải phương trình bậc hai tìm được \(x^2\))

Đạo hàm cấp hai:\(y''=20x^3-6x\)

Với x = 1 ta có: y''(1) = 14 > 0 nên hàm số đạt cực tiểu tại x = 1, giá trị cực tiểu yct = y(1) = -1

Với x = -1 ta có: y''(-1) = -14 < 0 hàm số đạt cực đại tại x = -1, giá trị cực đại ycđ = y(-1) = 3

Chứng minh rằng hàm số \(y = \sqrt {\left| x \right|} \) không có đạo hàm tại x = 0 nhưng vẫn đạt cực tiểu tại điểm đó

Phương pháp giải

• Tính \( \mathop {\lim }\limits_{x \to {x_0}} \dfrac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) suy ra không tồn tại
• Chứng minh \(f(x)\ge f(0)\) với mọi \(x\in R\)

Hướng dẫn giải

\(\begin{array}{l}y = f\left( x \right) = \sqrt {\left| x \right|} = \left\{ \begin{array}{l}\sqrt x \,\,khi\,\,x \ge 0\\\sqrt { - x} \,\,khi\,\,x < 0\end{array} \right.\\
\mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{\sqrt x }}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{1}{{\sqrt x }} = + \infty \\
\mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{\sqrt { - x} }}{x} \\= \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{\sqrt { - x} }}{{ - {{\left( {\sqrt { - x} } \right)}^2}}} = \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{ - 1}}{{\sqrt { - x} }} = - \infty \\
\Rightarrow \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} \ne \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}
\end{array}\)

\(\Rightarrow\) Không tồn tại đạo hàm của hàm số đã cho tại \(x = 0\)

Dễ thấy \(f(x)=\sqrt {\left| x \right|}\ge 0\) với mọi \(x\in R\) và \(f(0)=0\) nên \(x=0\) chính là điểm cực tiểu của hàm số

Chứng minh rằng với mọi giá trị của tham số m, hàm số \(y = x^3 - mx^2 - 2x + 1\) luôn luôn có một điểm cực đại và một điểm cực tiểu

Phương pháp giải

• Hàm số bậc ba: \(y = a{x^3} + b{x^2} + cx + d\,(a \ne 0)\) có cực đại và cực tiểu khi và chỉ khi phương trình \(y'=0\) luôn có 2 nghiệm phân biệt \(x_1;x_2.\)
• Khi đó y' luôn đổi dấu khi đi qua 2 điểm \(x_1;x_2.\)
• Ta có: \(y' = 3a{x^2} + 2bx + c\)
• Xét phương trình: \(3a{x^2} + 2bx + c=0\)
• Biệt thức: \(\Delta {'_{y'}} = {b^2} - 3ac\)
• Như vậy với bài 4, ta chỉ cần chứng minh \(\Delta {'_{y'}} = {b^2} - 3ac>0\) với mọi m.

Hướng dẫn giải

Áp dụng, ta có lời giài chi tiết bài 4 như sau

Xét hàm số \(y = x^3 - mx^2 - 2x + 1\)

Tập xác định \(D=\mathbb{R}\)

\(y' = 3{x^2} - 2mx - 2\), \(\Delta {'_{y'}} = {m^2} + 6 > 0,\forall m\) nên phương trình y’ = 0 luôn có hai nghiệm phân biệt và y’ đổi dấu khi qua các nghiệm đó

Vậy hàm số luôn có một cực đại và một cực tiểu

Tìm a và b để các cực trị của hàm số \(y=\frac{5}{3}a^{2}x^{3}+2ax^{2}-9x+b\) đều là những số dương và \({x_0} =  - \frac{5}{9}\) là điểm cực đại.

Phương pháp giải

Đây là bài toán tìm tham số để hàm số có cực trị thỏa mãn điều kiện cho trước.

Với dữ kiện của đề bài, ta nhận định

• Nếu a = 0, hàm số đã cho sẽ trở thành hàm số bậc nhất và không có cực trị.
• Nếu a khác 0, hàm số đã cho là một hàm số bậc ba, ta áp dụng quy tắc 1 để tìm tham số a và b theo yêu cầu bài toán.

Hướng dẫn giải

Khai thác dữ kiện đề bài cho ta có lời giải chi tiết bài 5 như sau

- Với a = 0 hàm số trở thành y = - 9x+b không có cực trị

- Với \(a \ne 0\) ta có: \(y' = 5{a^2}{x^2} + 4ax - 9\)

\(y' = 0 \Leftrightarrow 5{a^2}{x^2} + 4ax - 9 \Leftrightarrow \left[ \begin{array}{l} x = - \frac{9}{{5a}}\\ x = \frac{1}{a} \end{array} \right.\)

+ Với a < 0 ta có bảng biến thiên:

Theo giả thiết \({x_0} =  - \frac{5}{9}\) là điểm cực đại nên \(\frac{1}{a}=-\frac{5}{9}\Leftrightarrow a=-\frac{9}{5}.\) 

Giá trị cực tiểu là số dương nên

\(y_{CT}=y\left ( -\frac{9}{5a} \right )=y(1)>0\)

\(\Leftrightarrow \frac{5}{3}\cdot \left ( -\frac{9}{5} \right )^{2}+2\cdot \left ( -\frac{9}{5} \right )-9+b>0\)

\(\Leftrightarrow b>\frac{36}{5}\)

+ Với a < 0 ta có bảng biến thiên

Vì \({x_0} =  - \frac{5}{9}\) là điểm cực đại nên \( - \frac{9}{{5a}} =  - \frac{5}{9} \Leftrightarrow a = \frac{{81}}{{25}}\)

Giá trị cực tiểu là số dương nên

\({y_{CT}} = y\left( {\frac{1}{a}} \right) = \frac{5}{{3a}} + \frac{2}{a} - \frac{9}{a} + b > 0\)\(\small \Leftrightarrow b>\frac{400}{243}\)

Vậy các giá trị a, b cần tìm là

\(\left\{ \begin{array}{l}
a =  - \frac{9}{5}\\
b > \frac{{36}}{5}
\end{array} \right. \vee \left\{ \begin{array}{l}
a = \frac{{81}}{{25}}\\
b > \frac{{400}}{{243}}
\end{array} \right.\)

Xác định giá trị của tham số m để hàm số \(y = \frac{{{x^2} + mx + 1}}{{x + m}}\) đạt cực đại tại x = 2

Phương pháp giải

Với dạng bài tập này ta sẽ ưu tiên sử dụng quy tắc 2 để giải, sau đó thử lại các tham số tìm được xem yêu cầu bài toán có thỏa mãn hay không

Tuy nhiên khi rơi vào các trường hợp sau

• Thứ nhất: \(y''(x_0)=0\) với mọi m, không được dùng quy tắc 2 phải chuyển qua dùng quy tắc 1
• Thứ hai: Tính đạo hàm cấp 2 phức tạp, nên ưu tiên sử dụng quy tắc 1

Hướng dẫn giải

Xét hàm số \(y = \frac{{{x^2} + mx + 1}}{{x + m}}\)

Tập xác định: \(D=\mathbb{R}\setminus \left \{ -m \right \}\) 

\(y' = \frac{{2{x^2} + 2mx + {m^2} - 1}}{{{{\left( {x + m} \right)}^2}}}\)

Nếu hàm số đạt cực đại tại x = 2 thì \(y'(2) = 0 \Leftrightarrow {m^2} + 4m + 3 = 0\)

\(\Leftrightarrow \left[ \begin{array}{l} m = - 1\\ m = - 3 \end{array} \right.\)

- Với m = -1,  ta có : \(y = \frac{{{x^2} - x + 1}}{{x - 1}}\)

\(y' = \frac{{{x^2} - 2x}}{{{{(x - 1)}^2}}};\,\,y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 2 \end{array} \right.\) 

Bảng biến thiên

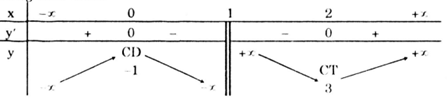
Vậy khi m = -1 hàm số không đạt cực đại tại x = 2

- Với m = -3, ta có: \(y = \frac{{{x^2} - 3x + 1}}{{x - 3}}\)

\(y' = \frac{{{x^2} - 6x + 8}}{{{{(x - 3)}^2}}};\,\,y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = 2\\ x = 4 \end{array} \right.\)

Bảng biến thiên

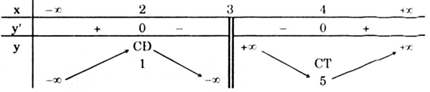
Vậy khi m = -3 hàm số đạt cực đại tại x = 2

Vậy m = -3 là giá trị cần tìm