Giải bài tập SGK Toán 12 Ôn tập Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ ĐTHS

Phát biểu các điều kiện đồng biến, nghịch biến của hàm số. Tìm các khoảng đơn điệu của các hàm số: \(y=-x^3+2x^2-x-7\); \(y=\frac{x-5}{1-x}\)

Các điều kiện đồng biến, nghịch biến của hàm số

- Điều kiện cần để hàm số đồng biến, nghịch biến

Cho hàm số \(y=f(x)\) có đạo hàm trên K

• Nếu \(f(x)\) đồng biến trên K thì \(f'(x)\geq 0\) với mọi \(x\in K\).
• Nếu \(f(x)\) nghịch biến trên K thì \(f'(x)\leq 0\) với mọi \(x\in K\).

- Điều kiện đủ để hàm số đồng biến, nghịch biến

Cho hàm số \(y=f(x)\) có đạo hàm trên K

• Nếu \(f'(x)\geq 0\) với mọi \(x\in K\) và \(f'(x)=0\) chỉ tại một số hữu hạn điểm thuộc K thì \(f(x)\) đồng biến trên K.
• Nếu \(f'(x)\leq 0\) với mọi \(x\in K\) và \(f'(x)=0\) chỉ tại một số hữu hạn điểm thuộc K thì \(f(x)\) nghịch biến trên K.

Hướng dẫn giải

+ Tìm khoảng đơn điệu của các hàm số \(y=-x^3+2x^2-x-7\)

Xét hàm số \(y=-x^3+2x^2-x-7\).

Tập xác định: D = R

\(y'=-3x^2+4x-1,y'=0\Leftrightarrow -3x^2+4x-1=0\Leftrightarrow \bigg \lbrack \begin{matrix} x=1\\ x=\frac{1}{3} \end{matrix}\)

Xét dấu y':

Vậy hàm số đồng biến trên khoảng \(\left( {\frac{1}{3};1} \right)\) và nghịch biến trên các khoảng \(\left( { - \infty ;\frac{1}{3}} \right);\left( {1; + \infty } \right)\)

+ Tìm khoảng đơn điệu của hàm số \(y=\frac{x-5}{1-x}\)

Xét hàm số \(y=\frac{x-5}{1-x}\).

Tập xác định: D = R \ {1}.

\(y'=\frac{1-x+x-5}{(1-x^2)^2}=\frac{-4}{(1-x)^2}<0 \ \ \ \forall x\in R \setminus \left \{ 1 \right \}\)

Vậy hàm số nghịch biến trên các khoảng \((-\infty ;1)\) và \((1; +\infty )\)

Nêu cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm. Tìm các cực trị của hàm số \(y=x^4-2x^2+2\)

Các cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm

- Quy tắc 1

• Tìm tập xác định.
• Tính \(f'(x)\). Tìm các điểm tại đó\(f'(x)=0\) hoặc \(f'(x)\) không xác định.
• Lập bảng biến thiên.
• Từ bảng biến thiên suy ra các điểm cực trị.

- Quy tắc 2

• Tìm tập xác định.
• Tính \(f'(x)\). Tìm các nghiệm \({x_i}\) của phương trình \(f'(x)=0\).
• Tính \(f''(x)\) và \(f''(x_i)\) suy ra tính chất cực trị của các điểm \({x_i}\).

- Chú ý: Nếu \(f''(x_i)=0\) thì ta phải dùng quy tắc 1 để xét cực trị tại \({x_i}\).

Hướng dẫn giải

Tìm các cực trị của hàm số \(y=x^4-2x^2+2\)

Xét hàm số: \(y=x^4-2x^2+2\)

Tập xác định: D = R

\(y'=4x^3-4x,y'=0\Leftrightarrow 4x^3-4x=0\)

\(\Leftrightarrow \bigg \lbrack \begin{matrix} x=-1\\ x=0\\ x=1 \end{matrix}\)

Xét dấy y'

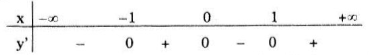
Vậy hàm số đạt cực đại tại x = 0, giá trị cực đại yCĐ = y(0) = 2; đạt cực tiểu tại x = -1 và x = 1, giá trị cực tiểu yCT = y(\(\pm\)1) =1.

Nêu cách tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số. Áp dụng để tìm các tiệm cận của đồ thị hàm số: \(y=\frac{2x+3}{2-x}\)

Cách tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số

- Đường thẳng \(y=b\) được gọi là tiệm cận ngang của đồ thị hàm số \(y = f(x)\) nếu thỏa mãn một trong các điều kiện sau

• \(\lim_{x\rightarrow -\infty } f(x) = b\)
• \(\lim_{x\rightarrow +\infty } f(x) = b\)

- Đường thẳng \(x=a\) được gọi là đường tiệm cận đứng của đồ thị hàm số \(y = f(x)\) nếu thỏa mãn một trong các điều kiện sau:

• \(\lim_{x\rightarrow a^+} f(x) = \pm \infty\)
• \(\lim_{x\rightarrow a^-} f(x) = \pm \infty\)

Hướng dẫn giải

Tìm tiệm cận của đồ thị hàm số \(y=\frac{2x+3}{2-x}\).

Vì \(\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  + \infty } \frac{{2x + 3}}{{2 - x}} =  - 2\)

Nên đường thẳng y = -2 là tiệm cận ngang của đồ thị hàm số.

Vì \(\lim_{x\rightarrow 2^-}y=\lim_{x\rightarrow 2^-} \frac{2x+3}{2-x}=+\infty,\) \(\lim_{x\rightarrow 2^+}y=\lim_{x\rightarrow 2^+} \frac{2x+3}{2-x}=-\infty\) 

Nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số

Nhắc lại sơ đồ khảo sát sự biến thiên và vẽ đồ thị của hàm số.

Hướng dẫn giải

Sơ đồ chung các bước khảo sát sự biến thiên và vẽ đồ thị hàm số

Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y=f(x)\)

- Bước 1: Tìm tập xác định của hàm số

- Bước 2: Khảo sát sự biến thiên: 

+ Xét chiều biến thiên của hàm số:

Tính đạo hàm \(f'(x)\). 

Tìm các điểm mà tại đó \(f'(x)=0\) hoặc không xác định.

Xét dấu đạo hàm \(f'(x)\) và suy ra chiều biến thiên của hàm số.

+ Tìm cực trị của hàm số.

+ Tính các giới hạn \(\lim_{x\rightarrow +\infty }y,\)

\(\lim_{x\rightarrow -\infty }y\) và các giới hạn có kết quả là vô cực (\(= \pm \infty\)), tìm các đường tiệm cận (nếu có)

- Bước 3: Vẽ đồ thị

+ Xác định các điểm đặc biệt: Giao với Ox, Oy điểm có tọa độ nguyên.

+ Nêu tâm đối xứng, trục đối xứng (nếu có).

Chú ý

- Đồ thị hàm số bậc ba nhận điểm \(I(x_0,f(x_0))\) với \(x_0\) là nghiệm phương trình \(f''(x_0)=0\) làm tâm đối xứng.

- Đồ thị hàm số phân thức bậc nhất/bậc nhất nhận giao của hai tiệm cận làm tâm đối xứng.

- Đồ thị hàm số lẻ nhận \(O(0;0)\) làm tâm đối xứng.

- Đồ thị hàm số chẵn nhận Oy làm trục đối xứng.

Cho hàm số \(y = 2x^2 + 2mx + m -1\) có đồ thị là \((C_m)\), \(m\) là tham số.

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 1

b) Xác định m để hàm số

- Đồng biến trên khoảng \((-1, +\infty )\)

- Có cực trị trên khoảng \((-1, +\infty )\)

c) Chứng minh rằng (Cm) luôn cắt trục hoành tại hai điểm phân biệt với mọi m.

Phương pháp giải

a) Khảo sát và vẽ đồ thị hàm số theo các bước đã được học.

b) Hàm số đồng biến trên \( (a; \, b)  \Leftrightarrow y' \ge 0\;\;\forall x \ne \left( {a;\;b} \right).\) 

+) Hàm số đồng biến trên \( (a; \, b)  \Leftrightarrow y' \le 0\;\;\forall x \ne \left( {a;\;b} \right).\) 

c) Chứng minh rằng \((C_m)\) luôn cắt trục hoành tại hai điểm phân biệt với mọi \(m\).

Hướng đẫn giải

Câu a: Với m = 1. Ta có hàm số: \(y = 2x^2 + 2x\)

1) Tập xác định: R

2) Sự biến thiên

Chiều biến thiên

\(y'=4x+2,\)

\(y'=0\Leftrightarrow 4x+2=0\Leftrightarrow x=-\frac{1}{2}\)

Xét dấu y'

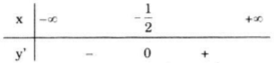
Vậy hàm số đồng biến trên khoảng \(\left ( -\frac{1}{2} ;+\infty \right )\), nghịch biến trên khoảng \(\left ( -\infty ;-\frac{1}{2} \right )\).

Cực trị: Hàm số đạt cực tiểu tại \(x=-\frac{1}{2}\), giá trị cực tiểu \(y_{CT}=y\left ( -\frac{1}{2} \right )=-\frac{1}{2}\). Hàm số không có cực đại.

Giới hạn

\(\lim_{x\rightarrow +\infty }y=\lim_{x\rightarrow +\infty }(2x^2+2x)=+\infty,\)

\(\lim_{x\rightarrow -\infty }y=\lim_{x\rightarrow -\infty }(2x^2+2x)=+\infty\)

Bảng biến thiên:

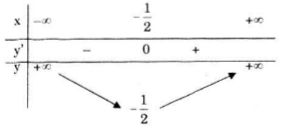
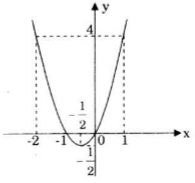
3) Đồ thị

Đồ thị cắt Ox tại các điểm (0;0) và (-1;0), cắt Oy tại điểm (0;0).

\(x=-2\Rightarrow y=4\)

\(x=1\Rightarrow y=4\)

Câu b: Xét hàm số \(y = 2x^2 + 2mx + m -1\)

\(y'=4x+2m,\)

\(y'=0\Leftrightarrow 4x+2m=0\Leftrightarrow x=-\frac{m}{2}\)

Bảng biến thiên

Từ bảng biến thiên ta suy ra

i) Hàm số đồng biến trên khoảng \((-1;+\infty )\) khi \(-\frac{m}{2}\leq -1\Leftrightarrow m\geq 2\).

ii) Hàm số có cực trị trên khoảng \((-1;+\infty )\) khi \(-\frac{m}{2}> -1\Leftrightarrow m< 2\).

Câu c: Phương trình hoành độ giao điểm của (Cm) với trục hoành

\(2{x^2} + 2mx + m - 1 = 0\)

Ta có

\(\Delta ' = {m^2} - 2m + 2 \)

\(= {(m - 1)^2} + 1 > 0,\forall m \in \mathbb{R}.\)

Vậy: (Cm) luôn cắt trục hoành tại hai điểm phân biệt.

a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) của hàm số: \(f(x) = -x^3+3x^2+9x+2\)

b) Giải bất phương trình f’(x-1) > 0

c) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x0, biết rằng f’’(x₀) = - 6.

Phướng pháp giải

a) Khảo sát và vẽ đồ thị hàm số qua các bước đã học.

b) Tính đạo hàm \(y=f'(x).\) Thay \(x-1\) vào vị trí của \(x\) để tính \(f'(x-1)\) và giải bất phương trình \(f'(x-1)>0.\)

c) Giải phương trình \(f''(x_0)=-6\) để tìm \(x_0.\) Sau đó viết phương trình tiếp tuyến của đồ thị hàm số \((C)\) theo công thức: \(y=y'(x_0)(x-x_0)+y(x_0).\)

Hướng dẫn giải

Câu a: Xét hàm số \(f(x)=-x^3+3x^2+9x+2\)

1) Tập xác định: D = R.

2) Sự biến thiên

Chiều biến thiên: \(f'(x)=-3x^2+6x+9.\)

\(f'(x)=0\Leftrightarrow -3x^2+6x+9=0\)

\(\Leftrightarrow \bigg \lbrack \begin{matrix} x=-1\\ x=3 \end{matrix}\)

Xét dấu f'(x)

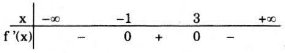
Vậy hàm số đồng biến trên khoảng (-1;3), nghịch biến trên khoảng \((-\infty ;-1)\) và \((3;+\infty )\).

Cực trị: Hàm số đạt cực đại tại x = 3 và giá trị cực đại yCĐ = y(3) = 29, đạt cực tiểu tại x = - 1 và giá trị cực tiểu yCT = y(-1) = -3.

Giới hạn

\(\begin{array}{l}
\mathop {\lim }\limits_{x \to  - \infty } y\\
 = \mathop {\lim }\limits_{x \to  - \infty } ( - {x^3} + 3{x^2} + 9x + 2)\\
 =  + \infty ,\\
\mathop {\lim }\limits_{x \to  + \infty } y\\
 = \mathop {\lim }\limits_{x \to  + \infty } ( - {x^3} + 3{x^2} + 9x + 2)\\
 =  - \infty 
\end{array}\)

Bảng biến thiên

3) Đồ thị

Ta có: y'' = - 6x + 6, y'' = 0 ⇔ x = 1. Vậy đồ thị hàm số nhận điểm (1;13) làm tâm đối xứng.

Đồ thị hàm số cắt Ox tại điểm (0;2).

Với \(x=-2\Rightarrow y=4\)

\(x=4\Rightarrow y=22\)

\(x=-3\Rightarrow y=29\)

Câu b: Ta có: \(f'(x)=-3x^2+6x+9\)

\(\Rightarrow f '(x-1)\)

\(=-3(x-1)^2+6(x-1)+9\)

\(=-3(x^2-2x+1)+6x-6+9\)

\(=-3x^2+6x-3+6x-6+9\)

\(=-3x^2+12x\)

Do đó: \(f'(x-1)> 0\Leftrightarrow -3x^2+12x>0\)

\( \Leftrightarrow 0 < x < 4\)

Câu c: Ta có: \(f''(x_0)=-6x_0+6\)

\(\Rightarrow f''(x_0)=-6\Leftrightarrow -6x_0+6=-6\)

\(\Leftrightarrow x_0=2\)

\(\Rightarrow f(x_0)=24\) và \(f'(x_0)=f'(2)=9\)

Vậy tiếp tuyến của đồ thị tại điểm x₀ theo yêu cầu bài toán là

\(y=9(x-2)+24\Leftrightarrow y=9x+6\)

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: \(y = x^3+ 3x^2+ 1.\)

b) Dựa vào đồ thị (C), biện luận số nghiệm của phương trình sau theo m: \(x^3+3x^2+1=\frac{m}{2}\).

c) Viết phương trình đường thẳng đi qua điểm cực đại và điểm cực tiểu của đồ thị (C).

Phương pháp giải

a) Khảo sát hàm số và vẽ đồ thị hàm số qua các bước đã học.

b) Số nghiệm của phương trình \(f(x) = \frac{m}{2}\) là số giao điểm của đồ thị hàm số \(y=f(x)\) và đường thẳng \(y=\frac{m}{2}.\) Dựa vào đồ thị để biện luận số nghiệm.

c) Xác định tọa độ các điểm cực trị của đồ thị hàm số.

Viết pt đường thẳng AB đi qua 2 điểm A, B ta làm như sau:

+ Tìm tọa độ \(\overrightarrow {AB} \) suy ra tọa độ VTPT của đt.

+ Viết pt đường thẳng theo công thức \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\)

Hướng dẫn giải

Câu a: \(y = x^3+ 3x^2+ 1\)

1) Tập xác định: D = R

2) Sự biến thiên

Chiều biến thiên

\(y' = 3{x^2} + 6x,y' = 0 \Leftrightarrow 3{x^2} + 6x = 0\)

\(\Leftrightarrow \bigg \lbrack \begin{matrix} x=-2\\ x=0 \end{matrix}\)

Xét dấu y'

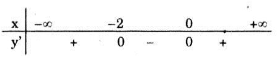
Vậy hàm số đồng biến trên các khoảng \((-\infty ;-2)\) và \((0;+\infty )\), nghịch biến trên khoảng (-2;0).

Cực trị: Hàm số đạt cực đại tại x = 0, giá trị cực đại y_CĐ = y(0) = 1; đạt cực tiểu tại x = -2, giá trị cực tiểu y_CT = y(-2) = 5.

Giới hạn

\(\begin{array}{l}
\mathop {\lim }\limits_{x \to  - \infty } y\\
 = \mathop {\lim }\limits_{x \to  - \infty } ({x^3} + 3{x^2} + 1) =  - \infty \\
\mathop {\lim }\limits_{x \to  + \infty } y\\
 = \mathop {\lim }\limits_{x \to  + \infty } ({x^3} + 3{x^2} + 1) =  + \infty 
\end{array}\)

Bảng biến thiên

3) Đồ thị

Ta có: y'' = 6x+6, y'' = 0 ⇔ x = - 1. Vậy đồ thị hàm số nhận điểm (-1;3) làm tâm đối xứng.

Đồ thị cắt Oy tại điểm (0;1).

Với x = -3 ⇒ y = 1

Với x = 1 ⇒ y = 5. 

Câu b: Số nghiệm của phương trình \(x^3+3x^2+1=\frac{m}{2} (*)\) là số giao điểm của đồ thị (C) và đường thẳng \(y=\frac{m}{2}\).

Dựa vào đồ thị trên ta có

+ Nếu \(\left[ \begin{array}{l}
\frac{m}{2} > 5\\
\frac{m}{2} < 1
\end{array} \right. \Leftrightarrow [\begin{array}{*{20}{c}}
{m > 10}\\
{m < 2}
\end{array}\) thì (*) có một nghiệm duy nhất.

+ Nếu \(\left[ \begin{array}{l}
\frac{m}{2} = 5\\
\frac{m}{2} = 1
\end{array} \right. \Leftrightarrow [\begin{array}{*{20}{c}}
{m = 10}\\
{m = 2}
\end{array}\) thì (*) có hai nghiệm phân biệt.

+ Nếu \(1< \frac{m}{2}< 5\Leftrightarrow 2< m< 10\)  thì (*) có ba nghiệm phân biệt.

Câu c: Ta thấy đồ thị hàm số có điểm cực đại là \(\displaystyle A(-2, 5)\), điểm cực tiểu là \(\displaystyle B(0, 1)\). 

Ta có: \(\overrightarrow {AB}  = \left( {2; - 4} \right) \Rightarrow \overrightarrow {{n_{AB}}}  = \left( {4;2} \right)\) là VTPT của AB.

AB đi qua A(-2;5) và nhận \(\overrightarrow {{n_{AB}}}  = \left( {4;2} \right)\) làm VTPT nên có pt:

\(4\left( {x + 2} \right) + 2\left( {y - 5} \right) = 0\)\( \Leftrightarrow 4x + 2y - 2 = 0\) \( \Leftrightarrow 2x + y - 1 = 0\)

Cho hàm số: \(f(x)= x^3– 3mx^2+ 3(2m-1)x + 1\) (\(m\) là tham số).

a) Xác định m để hàm số đồng biến trên một tập xác định.

b) Với giá trị nào của tham số m, hàm số có một cực đại và một cực tiểu.

c) Xác định m để f’’(x) > 6x.

Phương pháp giải

a) Hàm số \(y=f(x)\) đồng biến trên tập xác định \( \Leftrightarrow f'(x) \geq 0\) với mọi \(x\) thuộc tập xác định.

b) Hàm số có một cực đại và một cực tiểu \(\Leftrightarrow y'=0\) có hai nghiệm phân biệt.

c) Tính \(f''(x)\) sau đó giải bất phương trình \(f’’(x)>6x.\)

Hướng dẫn giải

Câu a: \(y=f(x)= x^3– 3mx^2+ 3(2m-1)x + 1\)

Tập xác định: \(D =\mathbb R\)

\(y’= 3x^2-6mx + 3(2m-1)\\ = 3(x^2– 2mx + 2m – 1)\)

Hàm số đồng biến trên \(D =\mathbb R \) \(⇔ y’ ≥ 0, ∀x ∈ R\)

\(⇔ x^2– 2mx + 2m - 1≥0, ∀x ∈\mathbb R\)

\(⇔ Δ’  \leq 0 \\  ⇔ m^2– 2m + 1  \leq 0 \\  ⇔ (m-1)^2\le 0 \\ ⇔ m =1.\)

(Vì \({\left( {m - 1} \right)^2} \ge 0,\forall m\) nên \({\left( {m - 1} \right)^2} \le 0\) chỉ xảy ra khi m-1=0)

Câu b: Hàm số có một cực đại và một cực tiểu

\(⇔\) phương trình \(y’= 0\) có hai nghiệm phân biệt

\( \Leftrightarrow {x^2} - 2mx + 2m - 1 = 0\) có hai nghiệm phân biệt

\(⇔ \Delta' >0 ⇔ (m-1)^2> 0 ⇔ m≠1.\)

Câu c: \(f’’(x) = 6x – 6m \)

\(f''(x) > 6x ⇔6x – 6m > 6x\)

\(⇔ -6m > 0\)

\(⇔ m < 0.\)

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số

\(f(x)=\frac{1}{2}x^4-3x^2+\frac{3}{2}\)

b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ là nghiệm của phương trình f’’(x) = 0

c) Biện luận theo tham số m số nghiệm của phương trình: \(x^4- 6x^2+ 3 = m.\)

Phương pháp giải

a) Khảo sát và vẽ đồ thị hàm số qua các bước đã học.

b) Giải phương trình \(\displaystyle f''(x)=0\) để tìm \(\displaystyle x_0.\) Sau đó viết phương trình tiếp tuyến của đồ thị hàm số \(\displaystyle (C)\) theo công thức: \(\displaystyle y=y'(x_0)(x-x_0)+y(x_0).\)

c) Đưa phương trình về dạng: \(\displaystyle {1 \over 2}{x^4} - 3{x^2} + {3 \over 2} = \frac{m}{2}. \) Sau đó dựa vào đồ thị ở câu a) để biện luận số nghiệm của phương trình.

Hướng dẫn giải

Câu a: \(f(x)=\frac{1}{2}x^4-3x^2+\frac{3}{2}\)

1) Tập xác định: D=R.

2) Sự biến thiên

Chiều biến thiên: \(f'(x)=2x^3-6x.\)

\(f'(x)=0 \Leftrightarrow 2x^3-6x=0\Leftrightarrow \Bigg \lbrack \begin{matrix} x=-\sqrt{3}\\ x=0\\ x=\sqrt{3} \end{matrix}\)

Xét dấu y'

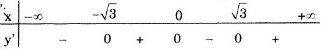
Vậy hàm số đồng biến trên các khoảng \((-\sqrt{3};0)\) và \((\sqrt{3};+\infty )\), nghịch biến trên các khoảng \((-\infty;-\sqrt{3})\) và \((0;\sqrt{3})\).

Cực trị

Hàm số đạt cực đại tại x = 0, giá trị cực đại \(y_{CD} = y(0)=\frac{3}{2}\), đạt cực tiểu tại \(x=-\sqrt{3}\) và \(x=\sqrt{3}\), giá trị cực tiểu \(y_{CT}=y(-\sqrt{3})=y(\sqrt{3})=-3\).

Giới hạn

\(\begin{array}{l}
\mathop {\lim }\limits_{x \to  - \infty } y\\
 = \mathop {\lim }\limits_{x \to  - \infty } \left( {\frac{1}{2}{x^4} - 3{x^2} + \frac{3}{2}} \right) =  + \infty \\
\mathop {\lim }\limits_{x \to  + \infty } y\\
 = \mathop {\lim }\limits_{x \to  + \infty } \left( {\frac{1}{2}{x^4} - 3{x^2} + \frac{3}{2}} \right) =  + \infty 
\end{array}\)

Bảng biến thiên

3) Đồ thị

Đồ thị hàm số nhận trục Oy là trục đối xứng.

Đồ thị cắt Oy tại điểm \(\left ( 0;\frac{3}{2} \right )\)

Ta có

x = 1 ⇒ y = -1

x = - 2 ⇒ y = \(\frac{{ - 5}}{2}\)

x = 2 ⇒ y = \(\frac{{ - 5}}{2}\)

x = -1 ⇒ y = -1

Câu b: Ta có: \(f''(x)=6x^2-6\)

\(f''(x)=0\Leftrightarrow 6x^2-6=0\Leftrightarrow \bigg \lbrack \begin{matrix} x=-1\\ x=1 \end{matrix}\)

+ Với  x = -1 ⇒ f(-1) = -1, f'(-1) = 4

Phương trình tiếp tuyến của (C) tại (-1; -1) là:

y = 4(x+1) - 1 ⇔ y = 4x + 3.

+ Với x = 1 ⇒ f(1) = -1, f'(1) = -4

Vậy phương trình tiếp tuyến của (C) tại (1; -1) là:

y = -4(x-1) -1 ⇔ y= -4x + 3.

Câu c: Ta có

\(x^4-6x^2+3=m\)

\(\Leftrightarrow \frac{1}{2}x^4-3x^2+\frac{3}{2}=\frac{m}{2}\) (*)

Số nghiệm của (*) là số giao điểm của (C) và đường thẳng \(y=\frac{m}{2}\)

Từ đồ thì (C) ta có

+ Nếu \(\frac{m}{2}<-3\Leftrightarrow m< -6\) thì (*) vô nghiệm.

+ Nếu \(\bigg \lbrack \begin{matrix} \frac{m}{2}=-3\\ \\ \frac{m}{2}>\frac{3}{2} \end{matrix}\Leftrightarrow \bigg \lbrack \begin{matrix} m=-6\\ m>3 \end{matrix}\) thì (*) có hai nghiệm phân biệt.

+ Nếu \(\frac{m}{2}=\frac{3}{2}\Leftrightarrow m=3\)  thì (*) có ba nghiệm phân biệt.

+ Nếu \( - 3 < \frac{m}{2} < \frac{3}{2} \Leftrightarrow  - 6 < m < 3\) thì (*) có bốn nghiệm phân biệt.

Cho hàm số \(y=-{{x}^{4}}+2m{{x}^{2}}-2m+1\) với (m tham số) có đồ thị \(\left( {{C}_{m}} \right)\).

a) Biện luận theo m số cực trị của hàm số.

b) Với giá trị nào của m thì \(\left( {{C}_{m}} \right)\) cắt trục hoành?

c) Xác định m để \(\left( {{C}_{m}} \right)\) có cực đại, cực tiểu.

Phương pháp giải

a) Số cực trị của hàm số là số nghiệm của phương trình: \(y'=0.\) Biện luận số cực trị của hàm số tức là biện luận số nghiệm của phương trình \(y'=0.\)

b) \((C_m)\) cắt trục hoành \(\Leftrightarrow \) phương trình \(y=f(x)=0\) có nghiệm.

c) Hàm số có cực đại và cực tiểu  \(\Leftrightarrow \) phương trình \(y'=f'(x)=0\) có 3 nghiệm phân biệt.

Hướng dẫn giải

Câu a: \(y = -x^4+ 2mx^2- 2m + 1\) \((C_m).\)

Tập xác định: \(D =\mathbb R\)

Ta có: \(y' = -4x^3+ 4mx = -4x (x^2- m)\)

\(\Rightarrow y'=0 \Leftrightarrow -4x(x^2-m)=0\) \( \Leftrightarrow  \left[ \begin{array}{l}x = 0\\{x^2} = m\end{array} \right..\)

+) Với \(m ≤ 0\) thì \(y’\) có một nghiệm \(x = 0\) và đổi dấu \(+\) sang \(–\) khi qua nghiệm này.

Do đó hàm số có một điểm cực đại là \(x = 0\)

+) Với \(m>0\) phương trình y ' = 0 có 3 nghiệm phân biệt nên hàm số có điểm 3 cực trị.

Do đó, hàm số có 2 điểm cực đại là \(x = ± \sqrt m\) và có một điểm cực tiểu là \(x = 0\).

Câu b: Phương trình hoành độ giao điểm của đồ thị hàm số \((C_m)\) và trục hoành là

\(\begin{array}{l}
- {x^4} + 2m{x^2} - 2m + 1 = 0\\
\Leftrightarrow \left( {{x^4} - 1} \right) - 2m\left( {{x^2} - 1} \right) = 0\\
\Leftrightarrow \left( {{x^2} - 1} \right)\left( {{x^2} + 1} \right) - 2m\left( {{x^2} - 1} \right) = 0\\
\Leftrightarrow \left( {{x^2} - 1} \right)\left( {{x^2} - 2m + 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
{x^2} - 1 = 0\\
{x^2} - 2m + 1 = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = \pm 1\\
{x^2} = 2m - 1
\end{array} \right..
\end{array}\)

Ta thấy phương trình hoành độ giao điểm luôn có nghiệm \(x = ± 1\) với mọi m nên \((C_m)\) luôn cắt trục hoành.

Câu c: Theo lời giải câu a, ta thấy ngay: với \(m > 0\) thì đồ thị \((C_m)\) có cực đại và cực tiểu.

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số \(y=\frac{x+3}{x+1}\)

b) Chứng minh rằng với mọi giá trị của m, đường thẳng y = 2x + m luôn cắt (C) tại hai điểm phân biệt M và N.

c) Xác định m sao cho độ dài MN là nhỏ nhất.

d) Tiếp tuyến tại một điểm S bất kỳ của (C) luôn cắt hai tiệm cận của (C) tại P và Q. Chứng minh rằng S là trung điểm của PQ.

Phương pháp giải

a) Khảo sát và vẽ đồ thi qua các bước đã được học.

b) Chứng minh phương trình hoành độ giao điểm của hai đồ thị hàm số có hai nghiệm phân biệt khác \(\displaystyle -1\) với mọi \(\displaystyle m.\)

c) Với hai điểm \(\displaystyle M\) và \(\displaystyle N\) tìm được ở câu trên, tính độ dài đoạn thẳng \(\displaystyle MN\) theo công thức: \(\displaystyle MN = \sqrt {{{\left( {{x_N} - {x_M}} \right)}^2} + {{\left( {{y_N} - {y_M}} \right)}^2}}  = \sqrt {f\left( x \right)} .\)

+) Khảo sát  và tìm giá trị nhỏ nhất của hàm số \(\displaystyle y=f(x)\) từ đó suy ra độ dài nhỏ nhất của \(\displaystyle MN.\)

d) Gọi \(\displaystyle S(x_0;\, y_0)\) là 1 điểm bất kì thuộc đồ thị hàm số \(\displaystyle (C).\) Khi đó phương trình tiếp tuyến của đồ thị hàm số tại \(\displaystyle S\) là: \(\displaystyle \Delta: \, y = y'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}.\)

+) Tìm các giao điểm \(\displaystyle P, \, \, Q\) của tiếp tuyến \(\displaystyle \Delta\) với các đường tiệm cận.

+) Khi đó \(\displaystyle S\) là trung điểm của \(\displaystyle PQ\Leftrightarrow \left\{ \begin{array}{l}{x_0} = \frac{{{x_P} + {x_Q}}}{2}\\{y_0} = \frac{{{y_P} + {y_Q}}}{2}\end{array} \right..\)

Hướng dẫn giải

Câu a: \(y=\frac{x+3}{x+1}\)

1) Tập xác định: R\{-1}.

2) Sự biến thiên: 

\(y'=\frac{x+1-x-3}{(x+1)^2}=\frac{-2}{(x+1)^2}<0 \ \ \forall x\neq -1\)

Vậy hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right).\)

Cực trị: Hàm số không có cực trị.

Tiệm cận

Vì \(\mathop {\lim }\limits_{x \to  - \infty } y = \mathop {\lim }\limits_{x \to  - \infty } \frac{{x + 3}}{{x + 1}} = 1\) nên đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.

Vì \(\mathop {\lim }\limits_{x \to  - 1} y = \mathop {\lim }\limits_{x \to  - 1} \frac{{x + 3}}{{x + 1}} =  - \infty ,\) \(\mathop {\lim }\limits_{x \to  - {1^ + }} y = \mathop {\lim }\limits_{x \to  - {1^ + }} \frac{{x + 3}}{{x + 1}} =  + \infty \) 

Nên đường thẳng x = -1 là tiệm cận đứng của đồ thị hàm số,

Bảng biến thiên:

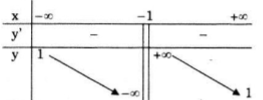
3) Đồ thị:

Đồ thị hàm số nhận điểm (-1;1) làm tâm đối xứng.

Đồ thị cắt Ox tại điểm (-3;0) cắt Oy tại điểm (0;3).

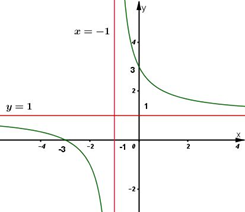
Câu b: Xét phương trình có nghiệm là hoành độ giao điểm của (C) và đường thẳng (d): \(\displaystyle y = 2x + m\) (1) 

\(\displaystyle \eqalign{
& {{x + 3} \over {x + 1}} = 2x + m \Leftrightarrow x + 3 = (2x + m)(x + 1) \cr 
& \Leftrightarrow 2{x^2} + (m + 1)x + m - 3 = 0,x \ne - 1 \cr} \)

\(\displaystyle Δ = (m+1)^2– 4.2(m-3) \\ = m^2+2m+1-8m+24 \\= m^2– 6m + 25\\ = (m-3)^2+ 16> 0 \)

\(\displaystyle \Rightarrow \) (1) luôn có hai nghiệm phân biệt.

Lại có:  \(\displaystyle f\left( { - 1} \right) = 2.{\left( { - 1} \right)^2} - \left( {m + 1} \right) + m - 3 =  - 2 \ne 0\) hay phương trình (1) có nghiệm khác \(\displaystyle -1\).

Vậy phương trình (1) luôn có 2 nghiệm phân biệt khác \(\displaystyle -1\) với mọi \(\displaystyle m.\)

Vậy (d) luôn cắt (C) tại hai điểm phân biệt \(\displaystyle M, N\) (hoành độ của \(\displaystyle M, N\) chính là nghiệm của (1)).

Câu c: Gọi \(\displaystyle M\left( {{x_M};\;{y_M}} \right)\) và \(\displaystyle N\left( {{x_N};\;{y_N}} \right)\) là hai giao điểm của \(\displaystyle (C)\) và đường thẳng \(\displaystyle y=2x+m.\)

Theo định lí Vi-et ta có:\(\displaystyle \left\{ \matrix{{x_M} + {x_N} = - {{m + 1} \over 2} \hfill \cr {x_M}.{x_N} = {{m - 3} \over 2} \hfill \cr} \right.\)

\(\displaystyle \begin{array}{l}
M{N^2} = {\left( {{x_M} - {x_N}} \right)^2} + {\left( {{y_M} - {y_N}} \right)^2}\\
= {\left( {{x_M} - {x_N}} \right)^2} + {\left[ {2{x_M} + m - \left( {2{x_N} + m} \right)} \right]^2}\\
= {\left( {{x_M} - {x_N}} \right)^2} + 4{\left( {{x_M} - {x_N}} \right)^2}\\
= 5{\left( {{x_M} - {x_N}} \right)^2}\\
= 5\left[ {{{\left( {{x_M} + {x_N}} \right)}^2} - 4{x_M}{x_N}} \right]\\
= 5\left[ {{{\left( { - \frac{{m + 1}}{2}} \right)}^2} - 4.\frac{{m - 3}}{2}} \right]\\
= 5\left( {\frac{{{m^2} + 2m + 1}}{4} - 2m + 6} \right)\\
= 5.\frac{{{m^2} - 6m + 25}}{4} \\ = \frac{5}{4}\left[ {\left( {{m^2} - 6m + 9} \right) + 16} \right]\\
= \frac{5}{4}\left[ {{{\left( {m - 3} \right)}^2} + 16} \right].
\end{array}\)

Ta có: \(\displaystyle {\left( {m - 3} \right)^2} \ge 0\;\forall \;m \Rightarrow {\left( {m - 3} \right)^2} + 16 \ge 16\)

\(\displaystyle \begin{array}{l}
\Rightarrow M{N^2} \ge \frac{5}{4}.16 = 20.\\
\Rightarrow MN \ge 2\sqrt 5 .
\end{array}\)

Dấu "=" xảy ra \(\displaystyle \Leftrightarrow m - 3 = 0 \Leftrightarrow m = 3.\)

Vậy độ dài \(\displaystyle MN\) nhỏ nhất bằng \(\displaystyle 2\sqrt5\) khi \(\displaystyle m=3.\)

Câu d: Giả sử \(\displaystyle S(x_0;y_0)\) là điểm bất kì thuộc (C)

Phương trình tiếp tuyến \(\displaystyle Δ\) của (C) tại \(\displaystyle S\) là:

\(\displaystyle \eqalign{
& y - y_0 = y'({x_0})(x - {x_0}) \cr 
& \Leftrightarrow y = {{ - 2} \over {{{({x_0} + 1)}^2}}}(x - {x_0}) + {{{x_0} + 3} \over {{x_0} + 1}} \cr} \)

Tiệm cận đứng: \(\displaystyle x=-1\) và tiệm cận ngang: \(\displaystyle y=1.\)

Giả sử \(\displaystyle Δ\) cắt tiệm cận ngang tại \(\displaystyle P(x_P;  1)\). Khi đó: 

\(\displaystyle \begin{array}{l}
\frac{{ - 2}}{{{{\left( {{x_0} + 1} \right)}^2}}}\left( {{x_P} - {x_0}} \right) + \frac{{{x_0} + 3}}{{{x_0} + 1}} = 1\\
\Leftrightarrow - 2{x_P} + 2{x_0} + x_0^2 + 4{x_0} + 3 = x_0^2 + 2{x_0} + 1\\
\Leftrightarrow - 2{x_P} = - 4{x_0} - 2\\
\Leftrightarrow {x_P} = 2{x_0} + 1\\
\Rightarrow P\left( {2{x_0} + 1;\;1} \right).
\end{array}\)

\(\displaystyle Δ\) cắt tiệm cận đứng tại \(\displaystyle Q( - 1; y_Q).\) Khi đó:

\(\displaystyle \begin{array}{l}
\frac{{ - 2}}{{{{\left( {{x_0} + 1} \right)}^2}}}\left( { - 1 - {x_0}} \right) + \frac{{{x_0} + 3}}{{{x_0} + 1}} = {y_Q}\\
\Leftrightarrow 2 + 2{x_0} + x_0^2 + 4{x_0} + 3 = {y_Q}{\left( {{x_0} + 1} \right)^2}\\
\Leftrightarrow x_0^2 + 6{x_0} + 5 = {y_Q}{\left( {{x_0} + 1} \right)^2}\\
\Leftrightarrow \left( {{x_0} + 1} \right)\left( {{x_0} + 5} \right) = {y_Q}{\left( {{x_0} + 1} \right)^2}\\
\Leftrightarrow {y_Q} = \frac{{{x_0} + 5}}{{{x_0} + 1}}.\\
\Rightarrow Q\left( { - 1;\;\frac{{{x_0} + 5}}{{{x_0} + 1}}} \right)
\end{array}\)

\(\displaystyle \Rightarrow \left\{ \begin{array}{l}
{x_P} + {x_Q} = 2{x_0} + 1 - 1 = 2{x_0} = 2{x_S}\\
{y_P} + {y_Q} = 1 + \frac{{{x_0} + 5}}{{{x_0} + 1}} = \frac{{2{x_0} + 6}}{{{x_0} + 1}} = \frac{{2\left( {{x_0} + 3} \right)}}{{{x_0} + 1}} = 2{y_0} = 2{y_S}.
\end{array} \right.\)

Vậy \(\displaystyle S\) là trung điểm của \(\displaystyle PQ\).

Cho hàm số \(f(x)=\frac{1}{3}x^3-\frac{1}{2}x^2-4x+6\)

a) Giải phương trình \(\displaystyle f’(sin x) = 0\)

b) Giải phương trình \(\displaystyle f’’(cos x) = 0\)

c) Viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ là nghiệm của phương trình \(\displaystyle f’’(x) = 0\).

Phương pháp giải

a) Tính đạo hàm \(f'(x)\) và \(f''(x)\). Thay \(\sin x\) vào giải phương trình \(f'(\sin x) =0\).

b) Thay \(\cos x\) vào giải phương trình \(f''(\cos x) =0\)

c) Giải phương trình \(f''(x)=0\) để tìm nghiệm \(x_0.\)

Lập phương trình tiếp tuyến của đồ thị hàm số theo công thức: \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + y\left( {{x_0}} \right).\)

Hướng dẫn giải

Câu a: \(\displaystyle f(x) = {1 \over 3}{x^3} - {1 \over 2}{x^2} - 4x + 6\)

\(\displaystyle \Rightarrow f’(x) = x^2– x – 4\)

\(\displaystyle \Rightarrow  f’’(x) = 2x – 1\)

Ta có

\(\displaystyle \eqalign{
& f'(s{\rm{inx}}) = 0 \Leftrightarrow {\sin ^2}x - {\mathop{\rm s}\nolimits} {\rm{in x}} - 4 = 0 \cr 
& \Leftrightarrow {\mathop{\rm s}\nolimits} {\rm{in x = }}{{1 \pm \sqrt {17} } \over 2}(1) \cr 
& Do{{1 - \sqrt {17} } \over 2} < - 1,{{1 + \sqrt {17} } \over 2} > 1 \cr} \)

Suy ra (1) vô nghiệm.

Câu b: Ta có

\(\displaystyle \eqalign{
& f''(cosx) = 0 \Leftrightarrow 2cosx - 1 = 0 \cr 
& \Leftrightarrow \cos x = {1 \over 2} = \cos {\pi \over 3} \cr 
& \Leftrightarrow x = \pm {\pi \over 3} + k2\pi ,k \in\mathbb Z \cr} \)

Câu c: \(f''\left( x \right) = 0 \Leftrightarrow 2x - 1 = 0 \Leftrightarrow x = \frac{1}{2}\)

Ta có

\(\displaystyle \eqalign{
& f'({1 \over 2}) = {1 \over 4} - {1 \over 2} - 4 = {{ - 17} \over 4} \cr 
&  f({1 \over 2}) = {1 \over 3}.{1 \over 8} - {1 \over 2}.{1 \over 4} - 4.{1 \over 2} + 6 = {{47} \over {12}} \cr} \)

Phương trình tiếp tuyến cần tìm có dạng

\(\displaystyle y = {{ - 17} \over 4}(x - {1 \over 2}) + {{47} \over {12}} \) \(\displaystyle  \Leftrightarrow y =  - {{17} \over 4}x + {{145} \over {24}}\)

Số điểm cực trị của hàm số là: \(\displaystyle y =  - {1 \over 3}{x^3} - x + 7\)

A. 1                             B. 0                              C. 3                              D. 2

Hướng dẫn giải

\(y’ = -x^2- 1 < 0, ∀x ∈\mathbb R\)

Hàm số luôn nghịch biến trên tập xác định. Do đó hàm số không có cực trị.

Chọn đáp án B

Số điểm cực đại của hàm số \(y = x^4+ 100\) là:

A. 0                             B. 1                               C. 2                             D. 3

Hướng dẫn giải

a có: \(y’= 4x^3 \Rightarrow  y'=0 \Leftrightarrow x = 0\).

Đạo hàm \(y’ < 0\)  với \(x < 0\) và \(y’ > 0\) với \(x > 0\).

BBT:

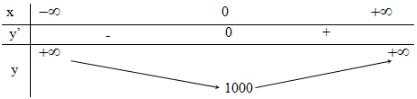
Vậy hàm số chỉ có \(1\) cực tiểu tại \(x = 0\) và không có điểm cực đại.

Vậy chọn đáp án A

Số đường tiệm cận của đồ thị hàm số \(\displaystyle y = {{1 - x} \over {1 + x}}\) là

A. 1                            B. 2                            C. 3                               D. 0

Hướng dẫn giải

Ta có: \(\mathop {\lim }\limits_{x \to  - {1^ - }} y =  + \infty ,\mathop {\lim }\limits_{x \to  - {1^ + }} y =  - \infty \).

\(\Rightarrow \)  \(x = -1\) là tiệm cận đứng của đồ thị hàm số.

\(\mathop {\lim }\limits_{x \to  \pm \infty } y \) \( = \mathop {\lim }\limits_{x \to  \pm \infty } \frac{{1 - x}}{{1 + x}} \) \(= \mathop {\lim }\limits_{x \to  \pm \infty } \frac{{\frac{1}{x} - 1}}{{\frac{1}{x} + 1}}=-1\)

\(\Rightarrow\)  \(y = - 1\) là tiệm cận ngang của đồ thị hàm số.

Vậy đồ thị có 2 tiệm cận.

Chọn đáp án B

Hàm số \(\displaystyle y = {{2x - 5} \over {x + 3}}\) đồng biến trên:

A. \(\displaystyle \mathbb R\)

B. \(\displaystyle (-∞, 3)\)

C. \(\displaystyle (-3, + ∞)\)

D. \(\displaystyle \mathbb R\backslash {\rm{\{ }} - 3\} \)

Hướng dẫn giải

Tập xác định của hàm số : \(\displaystyle D=\mathbb R\backslash {\rm{\{ }} - 3\} \)

Có \(\displaystyle y' = {{11} \over {{{(x + 3)}^2}}} > 0,\forall x \in D\)

Hàm số đồng biến trên \(\displaystyle \left( { - \infty ;\; - 3} \right) \) và \(\displaystyle \left( { - 3; + \infty } \right).\)

Chọn đáp án C

Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số là: \(\displaystyle y = {1 \over 3}{x^3} - 2{x^2} + 3x - 5\)

A. Song song với đường thẳng \(\displaystyle x = 1.\)

B. Song song với trục hoành.

C. Có hệ số góc dương.

D. Có hệ số góc bằng \(\displaystyle -1.\)

Hướng dẫn giải

Ta có: \(y’= x^2– 4x + 3 = 0 \) \(⇔ x = 1, x = 3\)

\(y’’ = 2x -4, \)

\(y’’(1) = -2 < 0\) nên x=1 là điểm cực đại của hàm số.

\(y’’(3) = 2 > 0\) nên x=3 là điểm cực tiểu của hàm số.

Phương trình tiếp tuyến tại điểm cực tiểu có hệ số góc \(y’(3) = 0\).

Do đó tiếp tuyến song song với trục hoành.

Chọn đáp án B