Giải bài tập SGK Toán 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Phần hướng dẫn giải bài tập giá trị lớn nhất và nhỏ nhất của hàm số sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập xác định GTLN, GTNN từ SGK Giải tích 12 Cơ bản và Nâng cao
Mục lục nội dung

1. Giải bài 1 trang 23 SGK Giải tích 12
Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số
a) \(y = x^3 - 3x^2 - 9x + 35\) trên các đoạn \([-4; 4]\) và \([0;5]\)
b) \(y = x^4 - 3x^2 + 2\) trên các đoạn \([0;3]\) và \([2;5]\)
c) \(y =\frac{ (2-x)}{(1-x)}\) trên các đoạn \([2;4]\) và \([-3;-2]\)
d) \(y =\sqrt{(5-4x)}\) trên đoạn \([-1;1]\)
Phương pháp giải
Quy tắc tìm GTLN và GTNN của hàm số \(f(x)\) liên tục trên một đoạn \([a;b].\)
- Tìm các điểm \(x_i\in (a ; b)\) (i = 1, 2, . . . , n) mà tại đó \(f'(x_i)=0\) hoặc \(f'(x_i)\) không xác định.
- Tính \(f(x),f(b),f(x_i)\) (i = 1, 2, . . . , n).
- Khi đó: \(\begin{array}{l}
\mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right) = \max \left\{ {f\left( a \right);f\left( b \right);f\left( {{x_i}} \right)} \right\};\\
\mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right) = \min \left\{ {f\left( a \right);f\left( b \right);f\left( {{x_i}} \right)} \right\}
\end{array}\)
Hướng dẫn giải
Câu a: Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = x^3 - 3x^2 - 9x + 35\) trên các đoạn \([-4; 4]\) và \([0;5]\)
Xét hàm số \(y = x^3 - 3x^2 - 9x + 35\)
Tập xác định \(D=\mathbb{R}\).
Hàm số liên tục trên các đoạn [-4;4] và [0;5] nên có GTLN và GTNN trên mỗi đoạn này.
Ta có: y’ = 3x2 – 6x – 9 = 3(x2 – 2x – 3)
- Trên đoạn [-4;4]
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = 3 \in \left[ { - 4;4} \right]\\ x = - 1 \in \left[ { - 4;4} \right] \end{array} \right.\)
Ta có: y(-4)=-41; y(4)=15; y(-1)=40; y(3)=8.
Vậy: Giá trị lớn nhất của hàm số là \(\mathop {\max y}\limits_{x \in \left[ { - 4;4} \right]} = y( - 1) = 40\).
Giá trị nhỏ nhất của hàm số là \(\mathop {\min y}\limits_{x \in \left[ { - 4;4} \right]} = y( - 4) = - 41.\)
- Trên đoạn [0;5]
\(y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x = 3 \in \left[ {0;5} \right]}\\ {x = - 1 \notin \left[ {0;5} \right]} \end{array}} \right.\)
Ta có: y(0)=35; y(5)=40; y(3)=8.
Vậy: Giá trị lớn nhất của hàm số là \(\mathop {\max y}\limits_{x \in \left[ {0;5} \right]} = y(5) = 40.\)
Giá trị nhỏ nhất của hàm số là \(\mathop {\min y}\limits_{x \in \left[ {0;5} \right]} = y(3) = 8.\)
Câu b: Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = x^4 - 3x^2 + 2\) trên các đoạn \([0;3]\) và \([2;5]\)
Xét hàm số \(y = x^4 - 3x^2 + 2\)
Tập xác định D=R
Hàm số liên tục trên các đoạn \([0;3]\) và \([2;5]\) nên có GTLN và GTNN trên các đoạn này:
Đạo hàm: y'=4x3-6x
- Trên đoạn [0;3]
\(y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x = - \sqrt {\frac{3}{2}} \notin \left[ {0;3} \right]}\\ {x = 0 \in \left[ {0;3} \right]}\\ {x = \sqrt {\frac{3}{2}} \in \left[ {0;3} \right]} \end{array}} \right.\)
Ta có: y(0)=2; \(y\left( {\sqrt {\frac{3}{2}} } \right) = - \frac{1}{4}\); y(3)=56.
Vậy: Giá trị lớn nhất của hàm số là \(\mathop {\max y}\limits_{x \in \left[ {0;3} \right]} = y\left( 3 \right) = 56.\)
Giá trị nhỏ nhất của hàm số là \(\mathop {\min y}\limits_{x \in \left[ {0;3} \right]} = y\left( {\sqrt {\frac{3}{2}} } \right) = - \frac{1}{4}.\)
- Trên đoạn [2;5]
\(y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x = - \sqrt {\frac{3}{2}} \notin \left[ {2;5} \right]}\\ {x = 0 \notin \left[ {2;5} \right]}\\ {x = \sqrt {\frac{3}{2}} \notin \left[ {0;3} \right]} \end{array}} \right.\)
Ta có: y(2)=6; y(5)=552
Vậy: Giá trị lớn nhất của hàm số là \(\mathop {\max y}\limits_{x \in \left[ {2;5} \right]} = y\left( 6 \right) = 552.\)
Giá trị nhỏ nhất của hàm số là \(\mathop {\min y}\limits_{x \in \left[ {2;5} \right]} = y\left( 2 \right) = 6.\)
Câu c: Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y =\frac{ (2-x)}{(1-x)}\) trên các đoạn \([2;4]\) và \([-3;-2]\)
Xét hàm số \(y =\frac{ (2-x)}{(1-x)}\)
Hàm số có tập xác định D = R \{1} và liên tục trên các đoạn [2;4] và [-3;-2] thuộc D, do đó hàm số có GTLN, GTNN trên mỗi đoạn này.
Ta có : \(y' = \frac{1}{{{{\left( {1 - x} \right)}^2}}} > 0,\forall x \ne 1\)
- Trên đoạn [2;4]: \(y(2)=0;y(4)=\frac{2}{3}.\)
Vậy: Giá trị nhỏ nhất của hàm số là \(\mathop {\min y}\limits_{x \in \left[ {2;4} \right]} = y\left( 2 \right) = 0.\)
Giá trị lớn nhất của hàm số là \(\mathop {\max y}\limits_{x \in \left[ {2;4} \right]} = y\left( 4 \right) = \frac{2}{3}.\)
- Trên đoạn [-3;-2]: \(y(-3)=\frac{5}{4};y(-2)=\frac{4}{3}.\)
Vậy: Giá trị nhỏ nhất của hàm số là \(\mathop {\min y}\limits_{x \in \left[ { - 3;-2} \right]} = y\left( { - 3} \right) = \frac{5}{4}.\)
Giá trị lớn nhất của hàm số là\(\mathop {\max y}\limits_{x \in \left[ { - 3; - 2} \right]} = y\left( { - 2} \right) = \frac{4}{3}.\)
Câu d: Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y =\sqrt{(5-4x)}\) trên đoạn \([-1;1]\)
Xét hàm số \(y =\sqrt{(5-4x)}\)
Hàm số có tập xác định \({\rm{D = }}\left( { - \infty ;\frac{5}{4}} \right]\) nên xác định và liên tục trên đoạn [-1;1], do đó có GTLN, GTNN trên đoạn [-1;1].
Ta có:\(y' = - \frac{2}{{\sqrt {5 - 4x} }} < 0,\forall x \in \left[ { - 1;1} \right].\)
Trên đoạn [-1;1]: y(-1) = 3; y(1) = 1.
Vậy: Giá trị lớn nhất của hàm số là \(\mathop {\max }\limits_{x \in \left[ { - 1;1} \right]} y = y( - 1) = 3.\)
Giá trị nhỏ nhất của hàm số là \(\mathop {\min }\limits_{x \in \left[ { - 1;1} \right]} y = y(1) = 1.\)
2. Giải bài 2 trang 24 SGK Giải tích 12
Trong số các hình chữ nhật cùng có chu vi 16 cm, hãy tìm hình chữ nhật có diện tích lớn nhất.
Phương pháp giải
Với bài 2 ta có hai cách giải thường được sử dụng
- Cách 1: áp dụng bất đẳng thức cô-si đã học ở lớp 10.
- Cách 2: ứng dụng đạo hàm để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số như nội dung bài vừa học.
Hướng dẫn giải
Cách 1: Áp dụng bất đăng thức cô-si
Kí hiệu x, y thứ tự là chiều dài và chiều rộng của hình chữ nhật (0 < x, y < 16).
Khi đó x + y = 8.
Theo bất đẳng thức Cô-si, ta có:
\(8=x+y\geq 2 \sqrt {x.y}\Rightarrow xy\leq 16.\)
\(xy=16\Leftrightarrow x=y=4.\)
Vậy diện tích hình chữ nhật lớn nhất bằng 16 cm2 khi x = y = 4(cm), tức là khi hình chữ nhật là hình vuông.
Cách 2: Ứng dụng đạo hàm để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Gọi x,y lần lượt là chiều dài và chiều rộng của hình chữ nhật (8>x>0; 8>y>0).
Khi đó chu vi: p=2(x+y)=16 ⇔ x+y=8 ⇔ y=8-x.
Ta có diện tích của hình chữ nhật là S=x.y=x(8-x) ⇔ S=-x2+8x.
Xét hàm số: S(x) = -x2+8x trên khoảng (0,8) ta có:
S'=-2x+8; S'=0 ⇔ x=4
Bảng biến thiên:

Từ bảng biến thiên ta thấy hàm số đạt giá trị lớn nhất tại x=4 khi đó maxS = 16.
Với x=4 suy ra y=4.
Vậy hình vuông có cạnh bằng 4 là hình có diện tích lớn nhất.
3. Giải bài 3 trang 24 SGK Giải tích 12
Trong tất cả các hình chữ nhật cùng có diện tích 48 m2 , hãy xác định hình chữ nhật có chu vi nhỏ nhất.
Phương pháp giải
Với bài 3 ta có hai cách giải thường được sử dụng như sau:
- Cách 1: áp dụng bất đẳng thức cô-si đã học ở lớp 10.
- Cách 2: ứng dụng đạo hàm để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số như nội dung bài vừa học.
Hướng dẫn giải
Cách 1: Sử dụng bất đẳng thức cô-si:
Kí hiệu x, y thứ tự là chiều dài và chiều rộng của hình chữ nhật (x, y > 0).
Khi đó xy = 48.
Theo bất đẳng thức Cô-si, ta có :
\(x + y \ge 2\sqrt {xy} = 2\sqrt {48} = 8\sqrt 3 \)
\(x + y = 8\sqrt 3 \Leftrightarrow x = y = 4\sqrt 3 \)
Vậy chu vi hình chữ nhật nhỏ nhất bằng \(2\left( {x + y} \right) = 16\sqrt 3 \) (m) khi \(x = y = 4\sqrt 3 \) (m), tức là khi hình chữ nhật là hình vuông
Cách 2: Ứng dụng đạo hàm để tìm giá trị lớn nhất và nhỏ nhất của hàm số
Gọi x,y lần lượt là chiều dài và chiều rộng của hình chữ nhật (x>0,y>0)
Ta có:
Khi đó chu vi của hình chữ nhật là \(p=2(x+y) \Leftrightarrow p=2x+\frac{96}{x}.\)
Xét hàm số \(p(x)=2x+\frac{96}{x}.\) trên \(\left( {0; + \infty } \right).\)
\(p'(x) = 2 - \frac{{96}}{{{x^2}}};\,\,p'(x) = 0 \Leftrightarrow x = 4\sqrt 3 {\mkern 1mu}\) (do x>0).
Bảng biến thiên

Từ bảng biến thiên ta có: \(\min p = 16\sqrt 3\) khi \(x = 4\sqrt 3 \,\).
Với \(x = 4\sqrt 3 \,\Rightarrow y=\frac{48}{x}=4\sqrt 3\).
Vậy hình vuông có cạnh \(4\sqrt 3 \,\) là hình có chu vi nhỏ nhất theo yêu cầu bài toán
4. Giải bài 4 trang 24 SGK Giải tích 12
Tính giá trị lớn nhất của các hàm số sau
a) \(y=\frac{4}{1+x^2}\)
b) \(y=4x^3-3x^4\)
Phương pháp giải
Bài 4 yêu cầu tìm giá trị lớn nhất của hàm số mà không có miền cho trước thì ta hiểu yêu cầu bài tập là tập giá trị lớn nhất của hàm số trên tập xác định.
Để tìm GTLN, GTNN của hàm số \(y=f(x)\) xác định trên tập hợp D, ta tiến hành khảo sát sự biến thiên của hàm số trên D, rồi căn cứ vào bảng biến thiên của hàm số đưa ra kết luận về GTLN và GTNN của hàm số.
Hướng dẫn giải
Câu a: Tính giá trị lớn nhất của hàm số sau \(y=\frac{4}{1+x^2}\)
Tập xác định \(D=\mathbb{R}.\)
Đạo hàm: \(y' = - \frac{{8x}}{{{{\left( {1 + {x^2}} \right)}^2}}}\)..
\(y'=0\Leftrightarrow x=0\)
Bảng biến thiên

Từ bảng biến thiên ta thấy giá trị lớn nhất của hàm số là \(\max y = y(0) = 4.\)
Câu b: Tính giá trị lớn nhất của hàm số sau \(y=4x^3-3x^4\)
Tập xác định \(D=\mathbb{R}.\)
Đạo hàm y’ = 12x2 – 12x3 = 12x2 (1 – x).
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 1 \end{array} \right.\)
Bảng biến thiên

Từ bảng biến thiên ta thấy giá trị lớn nhất của hàm số là \(\max y = y(1) = 1\)
5. Giải bài 5 trang 24 SGK Giải tích 12
Tính giá trị nhỏ nhất của các hàm số sau
a) \(y = \left | x \right |\)
b) \(y = x+\frac{4}{x} ( x > 0)\)
Phương pháp giải
Với bài 5 ta áp dụng cách giải sau
Để tìm GTLN, GTNN của hàm số \(y=f(x)\) xác định trên tập hợp D, ta tiến hành khảo sát sự biến thiên của hàm số trên D, rồi căn cứ vào bảng biến thiên của hàm số đưa ra kết luận về GTLN và GTNN của hàm số.
Có nhiều trường hợp ta có thể nhìn vào hàm số và đánh giá ngay được giá trị lớn nhất và nhỏ nhất của hàm số, cụ thể ở đây là câu a bài 5
Hướng dẫn giải
Câu a: Tính giá trị nhỏ nhất của hàm số sau \(y = \left | x \right |\)
Cách 1: Ứng dụng đạo hàm
\[y = \left| x \right| = \left\{ \begin{array}{l}
x,\;\;x \ge 0\\
- x,\;\;x \le 0
\end{array} \right.\]
Tập xác định \(D=\mathbb{R}.\)
\(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f(x) - f(0)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{x}{x} = 1.\)
\(\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f(x) - f(0)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{ - x}}{x} = - 1.\)
Vậy hàm số không có đạo hàm tại x=0.
Bảng biến thiên:
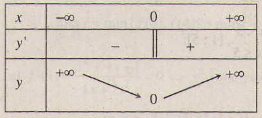
Từ bảng biến thiên ta thấy \(\min y = y(0) = 0.\)
Cách 2: Dùng tính chất của hàm số
Tập xác định \(D=\mathbb{R}.\)
Ta có: \(\left| x \right| \ge 0,\forall x \in\mathbb{R} ,\) dấu bằng xảy ra khi x=0. Vậy \(\min y = y(0) = 0.\)
Câu b: Tính giá trị nhỏ nhất của hàm số sau \(y = x+\frac{4}{x} ( x > 0)\)
Tập xác định \(D = \left( {0; + \infty } \right).\)
\(y' = 1 - \frac{4}{{{x^2}}} = \frac{{{x^2} - 4}}{{{x^2}}}\)
\(y' = 0 \Leftrightarrow x = 2.\)
Bảng biến thiên:
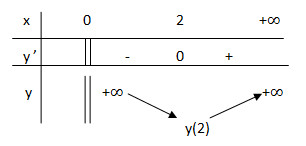
Vậy giá trị nhỏ nhất của hàm số là \(\mathop {\min }\limits_{x\left( {0; + \infty } \right)} = y(2) = 4.\)
Với câu b bài 5 ta cũng có thể dùng bất đẳng thức côsi để giải
Tham khảo thêm
- docx Giải bài tập SGK Toán 12 Bài 1: Sự đồng biến, nghịch biến của hàm số
- docx Giải bài tập SGK Toán 12 Bài 2: Cực trị của hàm số
- docx Giải bài tập SGK Toán 12 Bài 4: Đường tiệm cận
- docx Giải bài tập SGK Toán 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
- docx Giải bài tập SGK Toán 12 Ôn tập Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ ĐTHS
