Giải bài tập SGK Toán 5 Bài: Luyện tập chung

159 lượt xem
Share

Dựa theo cấu trúc SGK Toán 5, eLib xin mời các em học sinh tham khảo giải bài tập bài Luyện tập chung trang 127. Với các bài tập có lời giải chi tiết tương ứng với từng bài, hi vọng rằng đây sẽ là tài liệu giúp các em học tập tốt hơn.

Mục lục nội dung

Giải bài tập SGK Toán 5 Bài: Luyện tập chung

1. Giải bài 1 trang 127 SGK Toán 5

Cho hình thang vuông ABCD (xem hình vẽ) có AB = 4cm, DC = 5cm, AD = 3cm. Nối D với B ta được hai hình tam giác ABD và BDC.

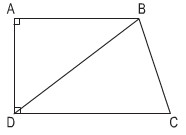
a) Tính diện tích mỗi hình tam giác đó.

b) Tính tỉ số phần trăm của diện tích hình tam giác ABD và diện tích hình tam giác BDC.

Phương pháp giải

a) Diện tích tam giác bằng nửa tích độ dài đáy nhân chiều cao

Đường cao của tam giác \(BDC\) chính bằng độ dài của đoạn \(AD\)

b) Tính tỉ số phần trăm của hai số \(a, \,\, b\) bằng cách lấy \(a\) chia \(b\) rồi nhân với \(100\)

Hướng dẫn giải

a) Diện tích tam giác \(ABD\) là:

\(\dfrac{AB \times AD}{2} = \dfrac{4 \times 3}{2} = 6 \, (cm^2)\)

Diện tích tam giác \(BDC\) (với độ dài đáy là \(DC\), độ dài đường cao bằng độ dài \(AD\)) là:

\(\dfrac{DC \times AD}{2} = \dfrac{5 \times 3}{2} = 7,5 \, (cm^2)\)

b) Tỉ số phần trăm của diện tích tam giác \(ABD\) và diện tích tam giác \(BDC\) là:

\(6 : 7,5 \times 100 = 80\%\)

Đáp số: 

a) \(6cm^2\) và \(7,5cm^2\)

b) \(80\%\)

2. Giải bài 2 trang 127 SGK Toán 5

Cho hình bình hành \(MNPQ\) (xem hình vẽ) có \(MN = 12cm\), chiều cao \(KH = 6cm\). So sánh diện tích hình tam giác \(KQP\) với tổng diện tích của hình tam giác \(MKQ\) và hình tam giác \(KNP.\)

Phương pháp giải

Bước 1: Tính diện tích tam giác \(KQP\) với độ dài đáy bằng độ dài \(MN\), chiều cao \(KH\)

Bước 2: Tính diện tích tam giác \(KQP\) với độ dài đáy \(MK\) chiều cao \(KH\)

Bước 3: Tính diện tích tam giác \(KNP\) với độ dài đáy \(KN\) chiều cao \(KH\)

Bước 4: Tính tổng diện tích hai tam giác \(KQP\) và \(KNP\) rồi so sánh với diện tích tam giác \(KQP\)

Hướng dẫn giải

Vì \(MNPQ\) là hình bình hành nên \( PQ = MN = 12cm\)

Diện tích tam giác \(KPQ\) là:

\(\dfrac{12 \times 6}{2} = 36 \, (cm^2)\)

Diện tích tam giác \(MKQ\) là:

\(\dfrac{MK \times KH}{2} = \dfrac{MK \times 6}{2} = 3 \times MK \, (cm^2)\)

Diện tích tam giác \(KNP\) là:

\(\dfrac{KN \times KH}{2} = \dfrac{KN \times 6}{2} = 3 \times KN \, (cm^2)\)

Tổng diện tích hai tam giác \(MKQ\) và \(KNP\) là:

\(3 \times MK + 3 \times NK = 3 \times (MK + NK) = 3 \times MN = 3 \times 12 = 36 \, (cm^2)\)

Vậy diện tích tam giác \(KQP\) bằng tổng diện tích hai tam giác \(MKQ\) và \(KNP\)

3. Giải bài 3 trang 127 SGK Toán 5

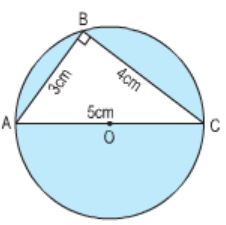
Trên hình bên, hãy tính diện tích phần đã tô màu của hình tròn.

Phương pháp giải

Bước 1: Tính bán kính hình tròn rồi tính diện tích hình tròn tâm O. Diện tích hình tròn bằng \(r \times r \times 3,14\)

Bước 2: Tính diện tích tam giác vuông ABC, diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông

Bước 3: Tính diện tích phần tô màu bằng diện tích hình tròn tâm O trừ đi diện tích tam giác ABC

Hướng dẫn giải

Bán kính hình tròn tâm O là:

\(5 : 2 = 2,5 \, (cm)\)

Diện tích hình tròn tâm O là:

\(2,5 \times 2,5 \times 3,14 = 19,625 \, (cm^2)\)

Diện tích tam giác vuông ABC là:

\(\dfrac{3 \times 4}{2} = 6 \, (cm^2)\)

Diện tích phần đã tô màu của hình tròn là:

\(19,625 - 6 = 13,625 \, (cm^2)\)

Đáp số: \(13,625cm^2\)

159 lượt xem
Share
Ngày:05/10/2020 Chia sẻ bởi:
TẢI VỀ XEM ONLINE

CÓ THỂ BẠN QUAN TÂM