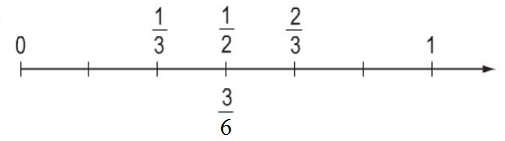Giải bài tập SGK Toán 5 Bài: Ôn tập về phân số

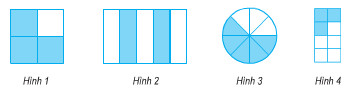
a) Viết phân số chỉ phần đã tô màu của mỗi hình dưới đây:

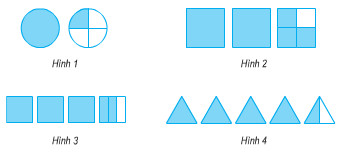
b) Viết hỗn số chỉ phần đã tô màu của mỗi hình dưới đây:

Phương pháp giải

- Phân số chỉ phần đã tô màu có tử số là số phần đã tô màu, mẫu số là tổng số phần bằng nhau trong hình

- Hỗn số chỉ số phần đã tô màu có phần nguyên là số hình đã tô màu trọn vẹn, phần phân số có tử số là số phần đã tô màu (trong hình chưa tô kín), mẫu số là tổng số phần bằng nhau trong hình chưa tô kín đó

Hướng dẫn giải

a)

Hình 1: $\bf \dfrac{3}{4}$           Hình 2: $\bf \dfrac{2}{5}$         

Hình 3: $\bf \dfrac{5}{8}$           Hình 4: $\bf \dfrac{3}{8}$

b)

Hình 1: $\bf 1 \dfrac{1}{4}$          Hình 2:  $\bf 2\dfrac{3}{4}$

Hình 3:  $\bf 3\dfrac{2}{3}$         Hình 4: $\bf 4\dfrac{1}{2}$

Rút gọn các phân số:

$\dfrac{3}{6}$         $\dfrac{18}{24}$         

$\dfrac{5}{35}$          $\dfrac{40}{90}$         

$\dfrac{75}{30}$

Phương pháp giải

Khi rút gọn phân số có thể làm như sau:

- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.

- Chia tử số và mẫu số cho số đó.

Cứ làm như thế cho đến khi nhận được phân số tối giản.

Hướng dẫn giải

$\dfrac{3}{6}= \dfrac{3:3}{6:3}= \dfrac{1}{2}$             $\dfrac{18}{24} = \dfrac{18:6}{24:6} = \dfrac{3}{4}$           

$\dfrac{5}{35}= \dfrac{5:5}{35:5} = \dfrac{1}{7}$            $\dfrac{40}{90} = \dfrac{40:10}{90:10}= \dfrac{4}{9}$           

$\dfrac{75}{30} = \dfrac{75:15}{30:15} = \dfrac{5}{2}$

Quy đồng mẫu số các phân số:

a) $\dfrac{3}{4}$ và $\dfrac{2}{5}$                      

b) $\dfrac{5}{12}$ và $\dfrac{11}{36}$

c) $\dfrac{2}{3}$, $\dfrac{3}{4}$ và $\dfrac{4}{5}$

Phương pháp giải

Khi quy đồng mẫu số hai phân số có thể làm như sau:

- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.

- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.

Hướng dẫn giải

a) $\dfrac{3}{4}=\dfrac{3 \times 5}{4 \times  5}= \dfrac{15}{20}$

$\dfrac{2}{5}=\dfrac{2 \times  4}{5 \times 4}=\dfrac{8}{20}$

b) $\dfrac{5}{12}=\dfrac{5 \times 3}{12 \times 3}=\dfrac{15}{36}$

Giữ nguyên phân số $\dfrac{11}{36}.$ 

c) $\dfrac{2}{3}=\dfrac{2 \times 4 \times 5}{3 \times 4 \times5}=\dfrac{40}{60}$      

$\dfrac{3}{4}=\dfrac{3 \times 3 \times 5}{4 \times 3 \times 5}=\dfrac{45}{60}$

$\dfrac{4}{5}=\dfrac{4 \times 3 \times 4}{5 \times 3 \times 4}=\dfrac{48}{60}$

Điền dấu thích hợp $(>;\; <;\;=)$ vào chỗ chấm:

$\dfrac{7}{12}....\dfrac{5}{12}$

$\dfrac{2}{5}.....\dfrac{6}{15}$

$\dfrac{7}{10}....\dfrac{7}{9}$

Phương pháp giải

Áp dụng các quy tắc so sánh phân số:

- Nếu hai phân số có cùng mẫu số, phân số nào có tử số lớn hơn thì phân số đó lớn hơn và ngược lại.

- Nếu hai phân số có cùng tử số, phân số nào có mẫu số lớn hơn thì phân số đó bé hơn và ngược lại.

- Nếu hai phân số không cùng mẫu số, ta có thể quy đồng mẫu số rồi so sánh hai phân số sau khi quy đồng.

Hướng dẫn giải

+) $\dfrac{7}{12}  > \dfrac{5}{12}$ (vì $7>5$).

+) Ta có: $\dfrac{2}{5}= \dfrac{2 \times 3}{5 \times 3} = \dfrac{6}{15}$ 

Vậy $\dfrac{2}{5} = \dfrac{6}{15}$.

+) $\dfrac{7}{10} < \dfrac{7}{9}$ (vì $10>9$).

Viết phân số thích hợp vào vạch giữa $\dfrac {1}{3}$ và $\dfrac {2}{3}$ trên tia số:

Phương pháp giải

Ta thấy: từ vạch $0$ đến vạch $1$ được chia thành $6$ phần bằng nhau. Ta sẽ quy đồng hai phân số $\dfrac {1}{3}$ và $\dfrac {2}{3}$ với mẫu số chung là $6$ rồi tìm phân số ở giữa hai phân số đó.

Hướng dẫn giải

Ta thấy: từ vạch $0$ đến vạch $1$ được chia thành $6$ bằng nhau. Quy đồng hai phân số $\dfrac {1}{3}$ và $\dfrac {2}{3}$ với mẫu số chung là $6$ ta có:

 $\dfrac {1}{3} = \dfrac{1 \times 2}{3\times 2 }= \dfrac {2}{6}$ ;    $\dfrac {2}{3} = \dfrac{2 \times 2}{3\times 2 }= \dfrac {4}{6}$.

Mà: $\dfrac {2}{6} < \dfrac{3}{6}< \dfrac {4}{6}$

Do đó vạch ở giữa $\dfrac {1}{3}$ và $\dfrac {2}{3}$ ứng với phân số $\dfrac {3}{6}$ hoặc phân số $\dfrac {1}{2}$ (vì rút gọn phân số $\dfrac {3}{6}$ ta được phân số tối giản $\dfrac {1}{2}$).