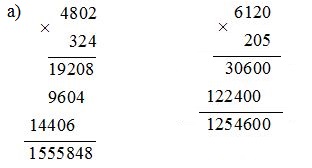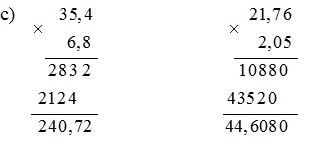Giải bài tập SGK Toán 5 Bài: Phép nhân

99 lượt xem
Share

Để các em học sinh lớp 5 có thêm thật nhiều tài liệu ôn tập môn Toán, đội ngũ eLib đã biên soạn và tổng hợp nội dung giải bài tập bài Phép nhân SGK bên dưới đây. Tài liệu gồm 4 bài tập có phương pháp và đáp án chi tiết đi kèm sẽ giúp các em vừa làm bài vừa đối chiếu đáp án từ đó có kế hoạch học tập phù hợp cho bản thân.

Mục lục nội dung

Giải bài tập SGK Toán 5 Bài: Phép nhân

1. Giải bài 1 trang 162 SGK Toán 5

Tính:

a) \(4802 × 324 \)                   

\(6120 × 205 \)

b) \(\dfrac{4}{17} × 2\)

\(\dfrac{4}{7} × \dfrac{5}{12}\)

c) \(35,4 × 6,8 \) 

\(21,76 × 2,05\)

Phương pháp giải

- Muốn nhân hai số tự nhiên ta đặt tính rồi tính sao cho các chữ số ở cùng một hàng thì thẳng cột với nhau, sau đó nhân theo thứ tự từ phải sang trái.

- Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.

- Muốn nhân hai số thập phân ta đặt tính rồi nhân như nhân các số tự nhiên, sau đó đếm xem trong phần thập phân của cả hai thừa số có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.

Hướng dẫn giải

b) \(\dfrac{4}{17}\times  2  = \dfrac{8}{17}\)

\(\dfrac{4}{7} \times \dfrac{5}{12} = \dfrac{4 \times 5}{7 \times 12}= \dfrac{20}{84} = \dfrac{5}{21}\)

2. Giải bài 2 trang 162 SGK Toán 5

Tính nhẩm:

a) \(3,25 × 10\) 

\(3,25 × 0,1\)

b) \(417,56 \times 100\) 

\(417,56 \times 0,01\)

c) \(28,5 \times 100\) 

\(28,5 \times 0,01\)

Phương pháp giải

- Muốn nhân một số thập phân với \(10, 100, 1000, ...\) ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba, ... chữ số.

- Muốn nhân một số thập phân với \(0,1; 0,01; 0,001; ...\) ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, ... chữ số. 

Hướng dẫn giải

a) \(3,25 × 10 = 32,5\)

\(3,25 × 0,1 = 0,325\)

b) \(417,56 \times 100 = 41756\) 

\(417,56 × 0,01 = 4,1756\)

c) \(28,5 × 100 = 2850\) 

\(28,5 × 0,01 = 0,285\)

3. Giải bài 3 trang 162 SGK Toán 5

Tính bằng cách thuận tiện nhất:

a) \(2,5 × 7,8 × 4\)

b) \(0,5 × 9,6 × 2\)

c) \(8,36 × 5 × 0,2\)

d) \(8,3 × 7,9 + 7,9 × 1,7\)

Phương pháp giải

Áp dụng các tính chất của phép nhân như:

Tính chất giao hoán: \(a × b =  b × a\)

Tính chất kết hợp: \((a × b) × c = a × (b × c)\)

Nhân một tổng với một số: \((a + b) × c = a × c + b × c.\)

Hướng dẫn giải

a) \(2,5 × 7,8 × 4 = (2,5 × 4) × 7,8\) \( = 10 × 7,8 = 78  ;\)

b) \(0,5 × 9,6 × 2 = (0,5 × 2) × 9,6\) \( = 1 × 9,6 = 9,6 ;\)

c) \(8,36 × 5 × 0,2 = 8,36 × (5 × 0,2)\) \( = 8,36 × 1 = 8,36 ;\)

d) \(8,3 × 7,9 + 7,9 × 1,7 \) \(= (8,3 + 1,7) × 7,9 = 10 × 7,9 = 79.\)

4. Giải bài 4 trang 162 SGK Toán 5

Một ô tô và một xe máy khởi hành cùng một lúc và đi ngược chiều nhau. Ô tô đi từ \(A\) với vận tốc \(48,5\)km/giờ, xe máy đi từ \(B\) với vận tốc \(33,5\) km/giờ. Sau \(1\) giờ \(30\) phút ô tô và xe máy gặp nhau tại \(C\). Hỏi quãng đường \(AB\) dài bao nhiêu ki-lô-mét?

Phương pháp giải

Theo đề bài ta có chuyển động của hai xe là chuyển động ngược chiều nhau và xuất phát cùng lúc. Do đó, để giải bài này ta có thể làm như sau:

- Tính tổng vận tốc của hai xe.

- Tính độ dài quãng đường AB = tổng vận tốc hai xe \(\times \) thời gian đi để hai xe gặp nhau.

Hướng dẫn giải

Đổi: \(1\) giờ \(30\) phút \(= 1,5\) giờ.

Tổng vận tốc của ô tô và xe máy là:

\(48,5 + 33,5 = 82\) \((km/\)giờ)

Độ dài quãng đường \(AB\) là:

\(82 × 1,5 = 123\) \((km)\)

Đáp số: \(123km\).

99 lượt xem
Share
Ngày:06/10/2020 Chia sẻ bởi:
TẢI VỀ XEM ONLINE

CÓ THỂ BẠN QUAN TÂM