Giải bài tập SGK Toán 10 Ôn tập chương 5: Thống kê
Phần hướng dẫn giải bài tập Bài Ôn tập chương 5: Thống kê sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Đại số 10. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.
Mục lục nội dung
1. Giải bài 1 trang 129 SGK Đại số 10
2. Giải bài 2 trang 129 SGK Đại số 10
3. Giải bài 3 trang 129 SGK Đại số 10
4. Giải bài 4 trang 129 SGK Đại số 10
5. Giải bài 5 trang 130 SGK Đại số 10
6. Giải bài 6 trang 130 SGK Đại số 10
7. Giải bài 7 trang 130 SGK Đại số 10
8. Giải bài 8 trang 131 SGK Đại số 10
9. Giải bài 9 trang 131 SGK Đại số 10

1. Giải bài 1 trang 129 SGK Đại số 10
Chỉ rõ các bước để:
a) Lập bảng phân bố tần suất ghép lớp
b) Lập bảng phân bố tần số ghép lớp.
Hướng dẫn giải
Câu a: Các bước lập bảng phân bố tần suất ghép lớp:
Bước 1: Chia bảng số liệu thống kê rời rạc thành các lớp.
Bước 2: Ghi các số liệu thống kế của mỗi lớp ghép vào cột “tần số”.
Bước 3: Tính tỉ số (phần trăm) của tần số mỗi lớp chia cho tổng các số liệu thống kê, ghi kết quả vào cột “tần suất”.
Câu b: Các bước lập bảng phân bố tần số ghép lớp:
Bước 1: Chia bảng số liệu thống kê rời rạc thành các lớp.
Bước 2: Ghi các số liệu thống kế của mỗi lớp ghép vào cột “tần số”.
2. Giải bài 2 trang 129 SGK Đại số 10
Nêu rõ cách tính của: số trung bình cộng, số trung vị, mốt, phương sai và độ lệch chuẩn.
Hướng dẫn giải
Để tính được các số trung bình cộng, phương sai, độ lệch chuẩn, trước hết ta cần lập bảng phân bố (tần số, tần suất, tần số ghép lớp hoặc tần suất ghép lớp).
- Đối với bảng phân bố tần số:
- Số trung bình cộng:
\(\overline x ={1 \over n}({n_1}{x_1} + {n_2}{x_2} + ... + {n_k}{x_k}) \)
- Phương sai:
\({s^2} = \dfrac{1}{N}.\left( {{n_1}.{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}.{{\left( {{x_2} - \overline x } \right)}^2} + {n_3}.{{\left( {{x_3} - \overline x } \right)}^2} + ... + {n_k}.{{\left( {{x_k} - \overline x } \right)}^2}} \right)\)
- Độ lệch chuẩn
Bước 1: Tính phương sai : \(S^2\)
Bước 2: Căn bậc hai của \(S^2\). Đó là độ lệch chuẩn
- Đối với bảng phân bố tần suất:
- Số trung bình cộng:
\(\overline x = {f_1}{x_1} + {f_2}{x_2} + ... + {f_k}{x_k}\)
- Phương sai:
\({s^2} = {f_1}.{\left( {{x_1} - \overline x } \right)^2} + {n_2}.{\left( {{x_2} - \overline x } \right)^2} + {f_3}.{\left( {{x_3} - \overline x } \right)^2} + ... + {f_k}.{\left( {{x_k} - \overline x } \right)^2}\)
- Độ lệch chuẩn
Bước 1: Tính phương sai : \(S^2\)
Bước 2: Căn bậc hai của \(S^2\). Đó là độ lệch chuẩn
- Đối với bảng phân bố tần số ghép lớp:
- Số trung bình cộng:
\( \overline x= {1 \over n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{x_k}) \)
- Phương sai:
\({s^2} = \frac{1}{N}.\left( {{n_1}.{{\left( {{c_1} - \bar x} \right)}^2} + {n_2}.{{\left( {{c_2} - \bar x} \right)}^2} + {n_3}.{{\left( {{c_3} - \bar x} \right)}^2} + ... + {n_k}.{{\left( {{c_k} - \bar x} \right)}^2}} \right)\)
- Độ lệch chuẩn
Bước 1: Tính phương sai : \(S^2\)
Bước 2: Căn bậc hai của \(S^2\). Đó là độ lệch chuẩn
- Đối với bảng phân bố tần suất ghép lớp:
- Số trung bình cộng:
\( \overline x = {f_1}{c_1} + {f_2}{c_2} + ... + {f_k}{c_k}\)
- Phương sai:
\({s^2} = {f_1}.{\left( {{c_1} - \overline x } \right)^2} + {n_2}.{\left( {{c_2} - \overline x } \right)^2} + {f_3}.{\left( {{c_3} - \overline x } \right)^2} + ... + {f_k}.{\left( {{c_k} - \overline x } \right)^2}\)
- Độ lệch chuẩn
Bước 1: Tính phương sai : \(S^2\)
Bước 2: Căn bậc hai của \(S^2\). Đó là độ lệch chuẩn
Trong tất cả các trường hợp
\(n\) là số các số liệu thống kê
\(n_i\) là tần số của giá trị \(x_i\)
\(c_i\) là giá trị trung tâm của lớp ghép
\(f_i\) là tần suất của giá trị \(x_i\), của giá trị trung tâm \(c_i\)
Câu b:
Số trung vị
Bước 1: Sắp thứ tự các số liệu thống kế thành dãy không giảm
Bước 2: Số đứng giữa của dãy này là số trung vị \(M_e\)
(Nếu trong dãy này có hai số đứng giữa thì số trung vị là trung bình cộng của hai số đứng giữa này).
Câu c:
Mốt: Đó là giá trị có tần số lớn nhất.
3. Giải bài 3 trang 129 SGK Đại số 10
Kết quả điều tra \(59\) hộ gia đình ở một vùng dân cư về số con của mỗi hộ gia đình là:
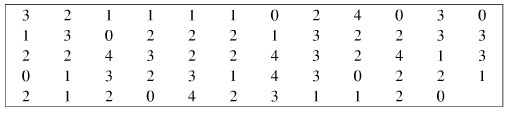
a) Lập bảng phân bố tần số và tần suất
b) Nêu nhận xét về số con của \(59\) gia đình đã được điều tra
c) Tính số trung bình cộng, số trung vị, mốt của các số liệu thống kế đã cho.
Phương pháp giải
Câu a:
- Liệt kê số con trong 1 hộ có thể có. (0, 1, 2, 3, 4)
- Đếm số hộ có 0, 1, 2, 3, 4 con điền vào cột tần số.
- Tính tỉ số phần trăm giữa tần số và tổng số hộ suy ra tần suất.
Câu b:
+) Dựa vào công thức số trung bình cộng, số trung vị và mốt được nêu ở câu 2 để làm bài toán.
Hướng dẫn giải
Câu a:
Bảng phân bố tần số và tần suất
Câu b:
Nhận xét: Số hộ có \(1\), \(2\) và \(3\) con chiếm hơn \(70\%\). Số hộ có \(2\) con chiếm tỉ lệ cao nhất \(32\%\).
Câu c:
Số trung bình: \(= {1 \over {59}}(8.0+13.1+19.2+13.3+6.4)\) \( ≈ 1,93\)
Mốt \(M_0= 2\) (con) (tần số lớn nhất bằng \(19\))
Số trung vị (số thứ 30) \(M_e= 2\)
4. Giải bài 4 trang 129 SGK Đại số 10
Cho các số liệu thống kê được ghi trong 2 bảng dưới đây:
Khối lượng (tính theo gam) của nhóm cá thứ 1
Khối lượng (tính theo gam) của nhóm cá thứ 2
a) Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 1 với các lớp là
[630; 635) ; [635;640) ; [640; 645) ; [645; 650) ; [650; 655)
b) Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 1 với các lớp là:
[638;642) ; [642; 646) ; [646;650) ; [650; 654] ;
c) Mô tả bảng phân bố tần suất ghép lớp đã được lập ở câu a) bằng cách vẽ biểu đồ tần suất hình cột và đường gấp khúc tần suất
d) Mô tả bảng phân bố tần suất ghép lớp đã được lập ở câu b) bằng cách vẽ biểu đồ tần số hình cột và đường gấp khúc tần số.
e) Tính số trung bình cộng, phương sai và độ lệch chuẩn của các bảng phân bố đã lập được
Từ đó, xét xem nhóm cá nào có khối lượng đồng đều hơn.
Hướng dẫn giải
Câu a:
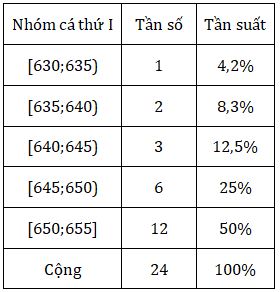
Bảng phân bố tần số và tần suất ghép lớp của nhóm cá thứ nhất.
Câu b:
Bảng phân bố tần số và tần suất ghép lớp của nhóm cá thứ hai
Câu c:
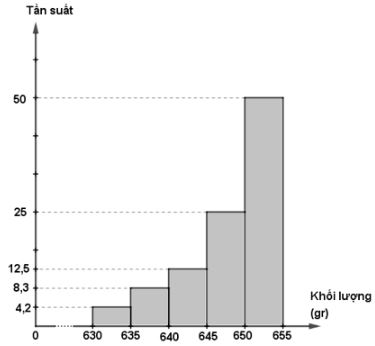
Biểu đồ hình cột và đường gấp khúc tần suất bảng phân phối ghép lớp trong câu a
Biểu đồ hình cột:
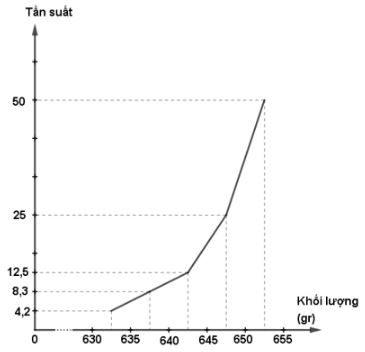
Đường gấp khúc tần suất:
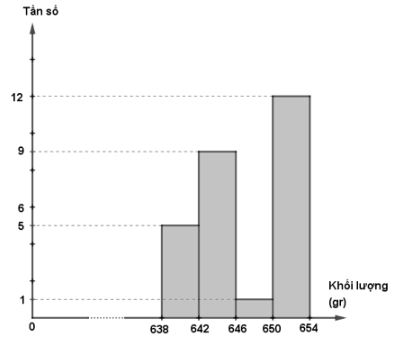
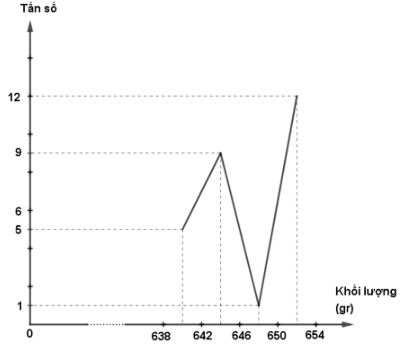
Câu d:
Biểu đồ hình cột và đường gấp khúc tần suất của bảng phân phối ghép lớp trong câu b
Câu e:
Số trung bình, phương sai và độ lệch chuẩn của bảng phân phối thứ nhất:
- Số trung bình là:
\(={1 \over {24}}[ 1.632,5 + 2.637,5 + 3.642,5 \)\(+ 647,5 + 12.652,5 ]≈ 647,92\) (gam)
- Phương sai:
\(\begin{array}{l} {s_1}^2= \frac{1}{{24}}\left[ \begin{array}{l} 1.{\left( {632,5 - 648} \right)^2} + 2.{\left( {637,5 - 648} \right)^2} + 3.{\left( {642,5 - 648} \right)^2}\\ + 6.{\left( {647,5 - 648} \right)^2} + 12.{\left( {652,5 - 648} \right)^2} \end{array} \right]\\ \approx 33,167 \end{array}\)
- Độ lệch chuẩn \(s_1≈ 5,76\)
- Số trung bình, phương sai và độ lệch chuẩn của bảng phân bố thứ hai:
- Số trung bình
\(\overline x = \frac{{5.640 + 9.644 + 1.648 + 12.652}}{{27}} \approx 647\)
- Phương sai:
\(\begin{array}{l} {s_1}^2 = \frac{1}{{27}}\left[ \begin{array}{l} 5.{\left( {640 - 647} \right)^2} + 9.{\left( {644 - 647} \right)^2}\\ + 1.{\left( {648 - 647} \right)^2} + 12.{\left( {652 - 647} \right)^2} \end{array} \right]\\ \approx 23,2 \end{array}\)
- Độ lệch chuẩn \( s_2= 4,82\)
Ta thấy số trung bình của hai nhóm cá xấp xỉ nhau. Nhưng phương sai, độ lệch chuẩn của nhóm cá thứ hai nhỏ hơn. Chứng tỏ khối lượng các con cá nhóm thứ hai đồng đều hơn nhóm thứ nhất.
5. Giải bài 5 trang 130 SGK Đại số 10
Cho dãy số liệu thống kế được ghi trong bảng sau:
Mức lương hàng năm của các cán bộ và nhân viên trong một công ty (đơn vị nghìn đồng)
a) Tìm mức lương trung bình của các cán bộ và nhân viên công ty, số trung bình của dãy số liệu.
b) Nêu ý nghĩa của số trung vị.
Hướng dẫn giải
Câu a:
Mức lương bình quân của nhân viên công ty là số trung bình của bảng lương.
\(={1 \over {12}}(29010 + 76000 + 20350.... \)\(+ 20960 + 125000)= 34087,5\) nghìn đồng
Câu b:
Số trung vị \(M_e= {{20960 + 21130} \over 2} = 21045\) (nghìn đồng)
Ý nghĩa: Số trung vị đại diện cho mức lương trung bình của nhân viên (vì trong trường hợp này chênh lệch giữa các số liệu quá lớn nên không thể lấy mức lương bình quân làm giá trị đại diện).
6. Giải bài 6 trang 130 SGK Đại số 10
Người ta tiến hành thăm dò ý kiến khách hàng về các mẫu 1, 2, 3, 4, 5 của một loại sản phẩm mới được sản xuất ở một nhà máy. Dưới đây là bảng phân bố tần số theo số phiếu tín nhiệm dành cho các mẫu kể trên.
a) Tìm mốt của bảng phân bố tần số đã cho
b) Trong sản xuất, nhà máy nên ưu tiên mẫu nào?
Phương pháp giải
- Mốt: Đó là giá trị có tần số lớn nhất.
- Nhà máy sẽ ưu tiên mẫu có tần số lớn nhất.
Hướng dẫn giải
Câu a:
Giá trị 1 (Mẫu số 1) là mốt của bảng phân bố. Vì có tần số \(2100\) lớn hơn các tần số còn lại.
Câu b:
Nhà máy ưu tiên sản xuất mẫu số 1 vì nhu cầu lớn hơn
7. Giải bài 7 trang 130 SGK Đại số 10
Cho bảng phân bố tần số.
Tiền thưởng (triệu đồng) cho các bộ và nhân viên trong một công ty.
Mốt của bảng phân bố đã cho là:
(A) Số 2
(B) Số 6
(C) Số 3
(D) Số 5
Phương pháp giải
Mốt: Đó là giá trị có tần số lớn nhất.
Hướng dẫn giải
Vì số tiền thưởng 3 triệu có tần số là 15 lớn nhất nên Mốt là 3 triệu đồng.
(C) đúng.
8. Giải bài 8 trang 131 SGK Đại số 10
Cho bảng phân bố tần số:
Tuổi của \(169\) đoàn viên thanh niên
Số trung vị của bảng phân phối đã cho là:
(A) Số \(18\)
(B) Số \(20\)
(C) Số \(19\)
(D) Số \(21\)
Phương pháp giải
Các bước tìm số trung vị
Bước 1: Sắp thứ tự các số liệu thống kế thành dãy không giảm
Bước 2: Số đứng giữa của dãy này là số trung vị \(M_e\) (Nếu trong dãy này có hai số đứng giữa thì số trung vị là trung bình cộng của hai số đứng giữa này).
Hướng dẫn giải
Sắp xếp các tuổi trên thành dãy không giảm :
18, 18, …, 18, 19, 19, …., 19, 20, 20, …, 20, 21, 21, …., 21, 22, 22, …, 22.
Dãy trên có 169 số nên số trung vị là số thứ 85 trong dãy trên.
Số thứ 85 trong dãy là 20.
Chọn B.
9. Giải bài 9 trang 131 SGK Đại số 10
Cho dãy số liệu thống kê \(21; 23; 24; 25; 22; 20\)
Số trung bình cộng của các số liệu thống kê đã cho bằng:
(A) \(23,5\)
(B) \(22\)
(C) \(22,5\)
(D) \(14\)
Phương pháp giải
Bảng phân bố rời rạc
\(\overline x ={1 \over n}({n_1}{x_1} + {n_2}{x_2} + ... + {n_k}{x_k})\)\( = {f_1}{x_1} + {f_2}{x_2} + ... + {f_k}{x_k}\)
Hướng dẫn giải
Số trung bình:
\({1 \over 6}(21 + 23 + 24 + 25 + 22 + 20) \)\(= 22,5\)
(C) đúng.
10. Giải bài 10 trang 131 SGK Đại số 10
Cho bảng thống kê: \(1,\, 2, \, 3, \, 4, \, 5,\, 6, \,7.\) Phương sai của các số liệu thống kê đã cho là:
(A) \(1\) (B) \(2\)
(C) \(3\) (D) \(4\)
Phương pháp giải
- Sử dụng công thức tính số trung bình:
\(\overline x ={1 \over n}({n_1}{x_1} + {n_2}{x_2} + ... + {n_k}{x_k}) \)
- Phương sai:
- Bước 1. Tìm số trung bình cộng.
- Bước 2. Bình phương các độ lệch của mỗi số liệu \({\left( {{x_i} - \overline x } \right)^2}\)
- Bước 3. Tìm trung bình cộng của \({\left( {{x_i} - \overline x } \right)^2}n_i\)
Kết quả là \(S^2\) (phương sai).
Hướng dẫn giải
- Số trung bình \({1 \over 7}(1 + 2 + 3 + 4 + 5 + 6 + 7) = 4\)
- Phương sai:
\({1 \over 7}{\rm{[}}{(1 - 4)^2} + {(2 - 4)^2} + {(3 - 4)^2} \)\(+ {(4 - 4)^2} + {(5 - 4)^{^2}} + {(6 - 4)^2} \)\(+ {(7 - 4)^2}{\rm{]}} = 4\)
Chọn (D)
11. Giải bài 11 trang 131 SGK Đại số 10
Ba nhóm học sinh gồm \(10 \)người, \(15\) người, \(25\) người. Khối lượng trung bình của mỗi nhóm lần lượt là : \(50kg,\, 38kg, \, 40kg.\) Khối lượng trung bình của ba nhóm học sinh là:
(A) \(41,4kg\)
(B) \(42,4 kg\)
(C) \(26 kg\)
(D) \(37 kg\)
Phương pháp giải
Sử dụng công thức tính số trung bình:
\(\overline x ={1 \over n}({n_1}{x_1} + {n_2}{x_2} + ... + {n_k}{x_k}) \)
Hướng dẫn giải
Khối lượng trung bình của cả ba nhóm học sinh: \(\frac{{50.10 + 38.15 + 40.25}}{{10 + 15 + 25}} = 41,4\) (kg)
Chọn (A)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
