Giải bài tập SGK Toán 10 Chương 2 Bài 3: Các hệ thức lượng trong tam giác và giải tam giác

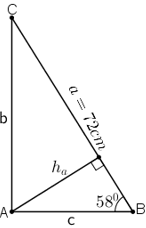
Cho tam giác \(ABC\) vuông tại \(A\), \(\widehat{B}= 58^0\) và cạnh \(a = 72 cm\). Tính \(\widehat{C}\), cạnh \(b\), cạnh \(c\) và đường cao \(h_a\)

Hướng dẫn giải

Theo định lí tổng \(3\) góc trong một tam giác ta có:

\(\eqalign{
& \widehat A + \widehat B + \widehat C = {180^0} \cr
& \Rightarrow \widehat C = {180^0} - \widehat A - \widehat B \cr&= {180^0} - {90^0} - {58^0} = {32^0} \cr} \)

Xét tam giác vuông \(ABC\) có:

\(\cos C = \frac{b}{a}\) \( \Rightarrow b =a. \cos C= 72.\cos {32^0} \) \(\Rightarrow b \approx 61,06cm\);

\(\sin C = \frac{c}{a} \) \(\Rightarrow c =a.\sin C= 72.\sin{32^0}\)\( \Rightarrow c \approx 38,15cm\)

\(a{h_a} = bc  \)\(\Rightarrow h_a =\frac{b.c}{a} = \frac{{61,06.38,15}}{{72}}\) \(\Rightarrow h_a ≈ 32,36cm.\)

Cho tam giác \(ABC\) biết các cạnh \(a = 52, 1cm\); \(b = 85cm\) và \(c = 54cm\). Tính các góc \(\widehat{A}\), \(\widehat{B}\), \(\widehat{C}\).

Hướng dẫn giải

Từ định lí cosin ta có: \({a^2} = {b^2} + {c^2} - 2bc.cosA.\)

Ta suy ra \(\cos A = \dfrac{b^{2}+c^{2}-a^{2}}{2bc}\)

\(= \dfrac{85^{2}+54^{2}-(52,1)^{2}}{2.85.54}\)

\(\Rightarrow \cos A  ≈ 0,809  \Rightarrow \widehat{A}≈ 36^0\) 

\(\begin{array}{l}
{b^2} = {c^2} + {a^2} - 2ca\cos B\\
\Rightarrow \cos B = \frac{{{c^2} + {a^2} - {b^2}}}{{2ca}}\\
= \frac{{{{54}^2} + 52,{1^2} - {{85}^2}}}{{2.54.52,1}} \approx - 0,2834
\end{array}\)

\(\Rightarrow  \widehat{B}≈  106^0 28’\) ;

\(\widehat{C} = {180^0} - \left( {A + B} \right) \) \(\approx {180^0} - \left( {{{36}^0} + {{106}^0}28'} \right)≈  37^032’\).

Cho tam giác \(ABC\) có \(\widehat{A}  = 120^0\) cạnh \(b = 8cm\) và \(c = 5cm\). Tính cạnh \(a\), và góc  \(\widehat{B}\), \(\widehat{C}\) của tam giác đó.

Hướng dẫn giải

Ta có   

\(\eqalign{
& {a^2}  = {b^2} + {c^2} - 2bc\cos A\cr &= {8^2} + {5^2} - 2.8.5.\cos{120^0} \cr&= 64 + 25 + 40 = 129 \cr
& \Rightarrow a = \sqrt {129} \approx 11,36cm \cr} \)

Theo định lí sin:

\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} \) \(\Rightarrow \sin B = \frac{{b\sin A}}{a} \approx \frac{{8\sin {{120}^0}}}{{11,36}} \approx 0,61 \) \(\Rightarrow B \approx {37^0}35'\)

\(A+B+C=180^0\) (Tổng ba góc trong một tam giác)

\(\Rightarrow \widehat{C}=180^0- (\widehat{A} + \widehat{B})\)\(=180^0-(120^0+37^0 35')\)  

\(\Rightarrow\widehat{C}= 22^0 25’.\)

Tính diện tích \(S\) của tam giác có số đo các cạnh lần lượt là \(7, \, \,9\) và \(12\).

Hướng dẫn giải

Diện tích tam giác là:

\(S = \sqrt {14\left( {14 - 7} \right)\left( {14 - 9} \right)\left( {14 - 12} \right)}  \) \(= \sqrt {980}  \approx 31,3\)

Tam giác \(ABC\) có  \(\widehat{A} = 120^0\). Tính cạnh \(BC\) cho biết cạnh \(AC = m\) và \(AB = n\).

Hướng dẫn giải

Áp dụng định lý hàm số \(\cos\) ta có:

\(\eqalign{ & BC^2=AB^2+AC^2-2AB.AC.\cos A \cr
&  = {m^2} + {n^2} - 2.m.n.\cos 120^0 \cr
& = {m^2} + {n^2} - 2mn.\left( { - \frac{1}{2}} \right) \cr &= {m^2} + {n^2} + m.n \cr
& \Rightarrow BC = \sqrt {{m^2} + {n^2} + m.n}. \cr} \)

Cho tam giác \(ABC\) biết cạnh \(a = 137,5cm; \widehat{B} = 83^0, \, \widehat{C} = 57^0.\) Tính góc \(A,\) bán kính \(R\) của đường tròn ngoại tiếp, cạnh \(b\) và \(c\) của tam giác.

Hướng dẫn giải

Ta có: \(\widehat{A} = 180^0- (\widehat{B}+ \widehat{C}) = 40^0\)

\(\dfrac{a}{{\sin A}} = 2R\) \( \Leftrightarrow R = \dfrac{a}{{2\sin A}} = \dfrac{{137,5}}{{2\sin {{40}^0}}} \approx 106,96\)

Áp dụng định lí \(\sin\):

\(\dfrac{a}{\sin A} = \dfrac{b}{\sin B} =  \dfrac{c}{\sin C}\), ta có:

\(b =\dfrac{a \sin B}{\sin A}= \dfrac{137,5.\sin83^{0}}{\sin40^0} ≈ 212,31cm.\)

\(c  =\dfrac{a \sin C}{\sin A}= \dfrac{137,5.\sin57^{0}}{\sin40^0} ≈ 179,40cm.\)

9. Giải bài 9 trang 59 SGK Hình học 10

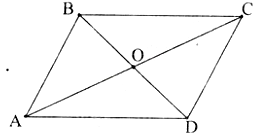
Cho hình bình hành \(ABCD\) có \(AB = a, BC = b ,BD = m\), và \(AC = n\). Chứng minh rằng:

\({m^2} + {n^2} = 2({a^2} + {b^2})\)

Hướng dẫn giải

Gọi O là giao điểm của AC và BD. Khi đó O là trung điểm của AC và BD.

Tam giác ABD có AO là đường trung tuyến.

Áp dụng định lí về đường trung tuyến:

\(A{O^2} = \frac{{2\left( {A{B^2} + A{D^2}} \right) - B{D^2}}}{4}\)

Mà O là trung điểm AC nên \(AO = \frac{{AC}}{2} = \frac{n}{2}\)

Thay \(OA = \frac{n}{2}, \, AB = a,\) \(AD = BC = b\) và \(BD = m\) ta được: 

\(\begin{array}{l}
{\left( {\frac{n}{2}} \right)^2} = \frac{{2\left( {{a^2} + {b^2}} \right) - {m^2}}}{4}\\
\Leftrightarrow \frac{{{n^2}}}{4} = \frac{{2\left( {{a^2} + {b^2}} \right) - {m^2}}}{4}\\
\Leftrightarrow {n^2} = 2\left( {{a^2} + {b^2}} \right) - {m^2}\\
\Leftrightarrow {m^2} + {n^2} = 2\left( {{a^2} + {b^2}} \right)
\end{array}\)

10. Giải bài 10 trang 60 SGK Hình học 10

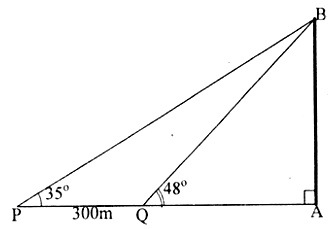
Hai chiếc tàu thủy \(P\) và \(Q\) cách nhau \(300m\).Từ \(P\) và \(Q\) thẳng hàng với chân \(A\) của tháp hải đăng \(AB\) ở trên bờ biển người ta nhìn chiều cao \(AB\) của tháp dưới các góc \(\widehat {BPA} = {35^0},\widehat {BQA} = {48^0}.\) Tính chiều cao của tháp.

Hướng dẫn giải

Tam giác ABQ vuông tại A có: \(\cot Q=\frac{AQ}{AB} \Rightarrow AQ = AB\cot48^0\)

Tam giác ABP vuông tại A có: \(\cot P = \frac{{AP}}{{AB}} \Rightarrow AP = AB\cot {35^0}\) 

\(\begin{array}{l}
\Rightarrow AP - AQ = AB\cot {35^0} - AB\cot {48^0}\\
\Leftrightarrow PQ = AB\left( {\cot {{35}^0} - \cot {{48}^0}} \right)\\
\Rightarrow AB = \frac{{PQ}}{{\cot {{35}^0} - \cot {{48}^0}}}\\
= \frac{{300}}{{\cot {{35}^0} - \cot {{48}^0}}}\\
= \frac{{300}}{{\frac{1}{{\tan {{35}^0}}} - \frac{1}{{\tan {{48}^0}}}}}
\end{array}\)

\( \approx {{300} \over {1,4281 - 0,9004}} \)\(\approx 568,457m.\)

11. Giải bài 11 trang 60 SGK Hình học 10

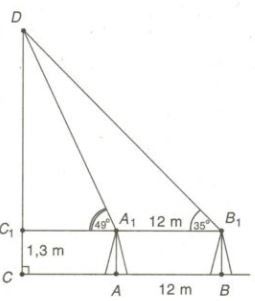
Muốn đo chiều cao của tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm \(A\) và \(B\) trên mặt đất có khoảng cách \(AB = 12m\) cùng thẳng hàng với chân \(C\) của tháp để đặt hai giác kế. Chân của giác kế có chiều cao \(h = 1,3m\). Gọi \(D\) là đỉnh tháp và hai điểm \(A_1, \, B_1\) cùng thẳng  hàng với \(C_1\) thuộc chiều cao \(CD\) của tháp. Người ta đo được \(\widehat {D{A_1}{C_1}} = {49^0}\) và \(\widehat {D{B_1}{C_1}} = {35^0}.\) Tính chiều cao của  \(CD\) của tháp đó.

Hướng dẫn giải

Ta có: \(A_1B_1=AB=12m.\)

Xét \(\Delta DC_1A_1\) có: \(\cot \widehat {D{A_1}{C_1}} = \frac{{{A_1}{C_1}}}{{{C_1}D}}\)

\(\Rightarrow {A_1}{C_1} = {C_1}D.\cot \widehat {D{A_1}{C_1}}\) \(=C_1D.\cot 49^0\)

Xét \(\Delta DC_1B_1\) có: \(\cot \widehat {D{B_1}{C_1}} = \frac{{{B_1}{C_1}}}{{{C_1}D}} \)

\(\Rightarrow {B_1}{C_1} = {C_1}D.\cot \widehat {D{B_1}{C_1}}\) \(=C_1D.\cot 35^0\)

Mà \(A_1B_1=C_1B_1-C_1A_1\)\(=C_1D.\cot 35^0-C_1D.\cot 49^0\)

\(=C_1D(\cot 35^0 - \cot 49^0).\)

\(\Rightarrow C_1D=\frac{A_1B_1}{\cot 35^0 - \cot 49^0}  =\frac{12}{\cot 35^0 - \cot 49^0}\)\(\approx 21,47 \, m. \)

Vậy chiều cao \(CD\) của tháp là: 

\(DC = C{C_1} + {C_1}D = 1,3 + 21,47\) \(= 22,77m.\)