Giải bài tập SGK Toán 10 Bài 4: Hệ trục tọa độ
Phần hướng dẫn giải bài tập Hệ trục tọa độ sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Hình học 10 Cơ bản và Nâng cao.
Mục lục nội dung

1. Giải bài 1 trang 26 SGK Hình học 10
Trên trục (O,  ) cho các điểm A, B, M có tọa độ lần lượt là \(-1, 2, 3, -2\) .
) cho các điểm A, B, M có tọa độ lần lượt là \(-1, 2, 3, -2\) .
a) Hãy vẽ trục và biểu diễn các điểm đã cho trên trục
b) Tính độ dài đại số của \(\overrightarrow{AB}\) và \(\overrightarrow{MN}\). Từ đó suy ra hai vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{MN}\) ngược hướng
Phương pháp giải
- Nếu hai điểm A, B trên trục \(\left( {O,\overrightarrow e } \right)\) có tọa độ lần lượt là a, b thì độ dài đại số \(\overline {AB} = {b - a} \).
- Số a là độ dài đại số của véc tơ \(\overrightarrow {AB} \) đối với trục \(\left( {O,\overrightarrow e } \right)\) thì \(\overrightarrow {AB} = a\overrightarrow e \).
Hướng dẫn giải
Câu a

Câu b
Đáp số: \(\overrightarrow{AB}\) = 3; \(\overrightarrow{MN}\) = -5. Từ đây ta có \(\overrightarrow{AB}\) = 3 , \(\overrightarrow{MN}\) = -5
, \(\overrightarrow{MN}\) = -5 và suy ra \(\overrightarrow{AB}\) = -
và suy ra \(\overrightarrow{AB}\) = -  \(\overrightarrow{MN}\) ⇒ \(\overrightarrow{AB}\) và \(\overrightarrow{MN}\) là hai vectơ ngược hướng.
\(\overrightarrow{MN}\) ⇒ \(\overrightarrow{AB}\) và \(\overrightarrow{MN}\) là hai vectơ ngược hướng.
2. Giải bài 2 trang 26 SGK Hình học 10
Trong mặt phẳng tọa độ các mệnh đề sau đúng hay sai?
a) \(\overrightarrow{a}= ( -3; 0)\) và \(\overrightarrow{i}= (1; 0)\) là hai vectơ ngược hướng
b) \(\overrightarrow{a}= ( 3; 4)\) và \(\overrightarrow{i}= (-3; -4)\) là hai vectơ đối nhau
c) \(\overrightarrow{a}= ( 5; 3)\) và \(\overrightarrow{i}= (3; 5)\) là hai vectơ đối nhau
d) hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau
Phương pháp giải
\(+ )\;\overrightarrow a = k\overrightarrow b \Rightarrow \overrightarrow a ,\;\overrightarrow b \) cùng phương. Với \(k < 0\) thì \(\overrightarrow a ,\;\overrightarrow b\) ngược hướng, với \(k > 0\) thì \(\overrightarrow a ,\;\overrightarrow b\) cùng hướng.
Hai véc tơ \(\overrightarrow a ,\overrightarrow b \) đối nhau nếu \(\overrightarrow a = - \overrightarrow b \)
Hướng dẫn giải
Câu a: Ta có: \(\overrightarrow a = - 3\overrightarrow i \) và \( -3 < 0\)
\( \Rightarrow \overrightarrow a ,\;\overrightarrow i \) là hai vecto ngược hướng.
Vậy a) đúng.
Câu b: Ta thấy: \(\overrightarrow a = - \overrightarrow b \)
\(\Rightarrow \overrightarrow a ,\;\overrightarrow b \) là hai vecto đối của nhau.
Vậy b) đúng.
Câu c: Ta có
\(\left\{ \begin{array}{l}
\overrightarrow a = 5\overrightarrow e + 3\overrightarrow j \\
\overrightarrow i = 3\overrightarrow e + 5\overrightarrow j
\end{array} \right. \\\Rightarrow \overrightarrow a \ne k\overrightarrow i \Rightarrow \overrightarrow a, \, \overrightarrow i \) không cùng phương.
Vậy c) sai.
Câu d: Dựa vào định nghĩa hai vecto bằng nhau ta thấy đáp án D đúng.
3. Giải bài 3 trang 26 SGK Hình học 10
Tìm tọa độ của các vec tơ sau:
a) \(\overrightarrow{a}=2\overrightarrow{j}\)
b) \(\overrightarrow{b}= -3\)
c) \(\overrightarrow{c}=3\overrightarrow{i} - 4\)
d) \(\overrightarrow{d}= 0,2\) \(\overrightarrow{i} + \sqrt{3}\overrightarrow{j}\)
Phương pháp giải
Cho vecto: \(\;\overrightarrow u = a\overrightarrow i + b\overrightarrow j \Rightarrow \overrightarrow u = \left( {a;\;b} \right).\)
Hướng dẫn giải
Câu a
Ta có = 2
= 2
+ 0
suy ra
= (2;0)
Câu b
= (0; -3)
Câu c
= (3; -4)
Câu d
\(\overrightarrow{d}= (0,2; - \sqrt{3})\)
4. Giải bài 4 trang 26 SGK Hình học 10
Trong mặt phẳng Oxy. Các khẳng định sau đúng hay sai?
a) Tọa độ của điểm A là tọa độ của vec tơ \(\overrightarrow{OA}\)
b) Điểm A nằm trên trục hoành thì có tung độ bằng 0
c) Điểm A nằm trên trục tung thì có hoành độ bằng 0
d) Hoành độ và tung độ của điểm A bằng nhau khi và chỉ khi A nằm trên tia phân giác của góc phần tư thứ nhất
Phương pháp giải
Dựa vào các khái niệm đã học trong sách giáo khoa để làm bài.
Hướng dẫn giải
Câu a: Đúng vì \(\overrightarrow {OA} = \left( {{x_A} - 0;\;{y_A} - 0} \right) = \left( {{x_A};\;y{ _A}} \right)\) chính là tọa độ điểm A.
Câu b: Đúng.
Mọi điểm trên trục hoành có tọa độ dạng (x;0).
Câu c: Đúng.
Mọi điểm trên trục tung có tọa độ dạng (0;y).
Câu d: Đúng vì tia phân giác của góc phần tư thứ nhất có phương trình là: \(y=x.\)
Mọi điểm thuộc đường thẳng này đều có y=x nên có tọa độ dạng (a;a) hay hoành độ và tung độ của chúng bằng nhau.
5. Giải bài 5 trang 27 SGK Hình học 10
Trong các mặt phẳng Oxy cho điểm (x0; y0)
a) Tìm tọa độ điểm A đối xứng với M qua trục Ox
b) Tìm tọa độ điểm B đối xứng với M qua trục Oy
c) Tìm tọa độ điểm C đối xứng với M qua gốc O
Phương pháp giải
Dựng hình suy ra tọa độ cần tìm.
Hướng dẫn giải
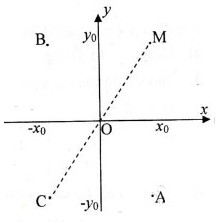
Câu a
Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0) ⇒ A(x0;-y0)
Câu b
Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) ⇒ B(-x0;y0)
Câu c
Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) ⇒ C(-x0;-y0)
6. Giải bài 6 trang 27 SGK Hình học 10
Cho hình bình hành ABCD có A(-1; -2), B(3;2), C(4;-1). Tìm tọa độ điểm D.
Phương pháp giải
Dựa vào tính chất của hình bình hành: ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {CD} = \overrightarrow {BA} \)
Các công thức sử dụng: \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right)\)
Hai véc tơ bằng nhau \(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}
{x_1} = {x_2}\\
{y_1} = {y_2}
\end{array} \right.\)
Hướng dẫn giải
.png)
Tứ giác ABCD là hình bình hành nên
\(\overrightarrow {CD} \) = \(\overrightarrow {BA} \)
Gọi (x; y) là tọa độ của D thì
\(\overrightarrow {CD} \) = (x-4; y+1)
\(\overrightarrow {BA} \)= (-4;4)
\(\overrightarrow {CD} \) = \(\overrightarrow {BA} \) \( \Leftrightarrow \left\{ \begin{array}{l}
x - 4 = - 4\\
y + 1 = - 4
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = 0\\
y = 5
\end{array} \right.\)
Vậy điểm D(0;-5) là điểm cần tìm
7. Giải bài 7 trang 27 SGK Hình học 10
Các điểm A'(-4; 1), B'(2;4), C(2, -2) lần lượt là trung điểm của các cạnh BC, CA và AB của tam giác ABC. Tính tọa độ các đỉnh của tam giác ABC. Chứng minh trọng tâm của các tam giác ABC và A'B'C' trùng nhau.
Phương pháp giải
- \(I\) là trung điểm của \(AB\) thì: \(\left\{ \begin{array}{l}
{x_I} = \frac{{{x_A} + {x_B}}}{2}\\
{y_I} = \frac{{{y_A} + {y_B}}}{2}
\end{array} \right..\)
- \(G\) là trọng tâm tam giác \(ABC\) thì: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right..\)
Hướng dẫn giải
A' là trung điểm của cạnh BC nên -4 = \(\frac{1}{2}\) (xB+ xC)
⇒ xB+ xC = -8 (1)
Tương tự ta có xA+ xC = 4 (2)
xB+ xC = 4 (3)
⇒ xA+ xB+ xC =0 (4)
Kết hợp (4) và (1) ta có: xA= 8
(4) và (2) ta có: xB= -4
(4) và (3) ta có: xC = -4
Tương tự ta tính được: yA = 1; yB = -5; yC = 7.
Vậy A(8;1), B(-4;-5), C(-4; 7).
Gọi G la trọng tâm tam giác ABC thì
xG = \(\frac{{8 - 4 - 4}}{3}\)= 0; yG = \(\frac{{1 - 5 +7}}{3}\) = 1 ⇒ G(0,1).
xG’ = \(\frac{{-4 +2+2}}{3}\); yG’ = \(\frac{{1+4-2}}{3}\) = 1 ⇒ G'(0;1)
Rõ ràng G và G' trùng nhau.
8. Giải bài 8 trang 27 SGK Hình học 10
Cho \(\overrightarrow{a}= (2; -2)\), \(\overrightarrow{b} = (1; 4)\). Hãy phân tích vectơ \(\overrightarrow{c} = (5; 0)\) theo hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}.\)
Phương pháp giải
Dựa vào công thức cộng các vecto để làm bài toán.
\(\overrightarrow c = m\overrightarrow a + n\overrightarrow b \)\(\Leftrightarrow \left\{ \begin{array}{l}
{x_c} = m{x_a} + n{x_b}\\
{y_c} = m{y_a} + n{y_c}
\end{array} \right..\)
Hướng dẫn giải
Giả sử ta phân tích được \(\overrightarrow{c}\) theo \(\overrightarrow{a}\) và \(\overrightarrow{b}\) tức là có hai số \(m, n\) để:
\(\overrightarrow{c}= m.\overrightarrow{a} + n.\overrightarrow{b}\).
Mà \(\overrightarrow{a}= (2; -2)\), \(\overrightarrow{b} = (1; 4)\) nên:
\(\begin{array}{l}
m\overrightarrow a = \left( {2m; - 2m} \right)\\
n\overrightarrow b = \left( {n;4n} \right)
\end{array}\)
Do đó \(\overrightarrow{c}= (2m+n; -2m+4n)\)
Vì \(\overrightarrow{c} =(5;0)\) nên ta có hệ:
\(\left\{\begin{matrix} 2m+n=5\\ -2m+4n=0 \end{matrix}\right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}
5n = 5\\
2m + n = 5
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
n = 1\\
2m + 1 = 5
\end{array} \right. \) \(\Leftrightarrow \left\{ \begin{array}{l}
m = 2\\
n = 1
\end{array} \right.\)
Vậy \(\overrightarrow{c} = 2\overrightarrow{a} + \overrightarrow{b}\
