Toán 12 Chương 3 Bài 1: Hệ tọa độ trong không gian
Việc học các kỹ năng giải Toán rất quan trọng đặc biệt là các em học sinh lớp 12. Vậy giải Toán như thế nào để phù hợp với tất cả các học sinh, các em có thể tự đọc các kiến thức và tự làm các ví dụ minh họa để nâng cao các kỹ năng giải Toán lớp 12 của mình thêm hiệu quả. Sau đây là các kiến thức cần nhớ và các bài tập minh họa bài hệ tọa độ trong không gian, mời các em cùng tham khảo.

1. Tóm tắt lý thuyết
1.1. Tọa độ của điểm và của vectơ
a) Hệ tọa độ
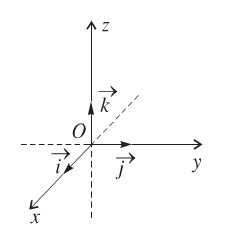
Trong không gian, cho ba trục xOx', yOy', zOz' vuông góc với nhau từng đôi một.
Các vectơ \(\overrightarrow i ,\,\,\overrightarrow j ,\,\overrightarrow k\) lần lượt là các vectơ đơn vị trên các trục xOx', yOy', zOz' với: \(\left | \vec{i} \right |=\left | \vec{j} \right |=\left | \vec{k} \right |=1.\)
Hệ trục như vậy được gọi là hệ trục tọa độ Oxyz, với O là gốc tọa độ.
b) Tọa độ của vectơ trong không gian
Trong không gian Oxyz, cho vectơ \(\vec{u}\) tồn tại duy nhất bộ số \((x,y,z)\) sao cho: \(\overrightarrow{u}=(x;y;z)\)\(\Leftrightarrow \vec{u}=x\vec{i}+y\vec{j}+z\vec{k}.\)
Bộ số: \((x,y,z)\) được gọi là tọa độ của vectơ \(\vec{u}\).
c) Tọa độ điểm trong không gian
Trong không gian Oxyz, cho điểm A tùy ý tồn tại duy nhất bộ số \((x_A,y_A,z_A)\) sao cho: \(A(x_A,y_A,z_A)\Leftrightarrow \overrightarrow{OA}=(x_A;y_A;z_A).\)
Bộ số \((x_A,y_A,z_A)\) được gọi là tọa độ điểm A.
1.2. Biểu thức tọa độ của các phép toán vectơ
Cho hai vectơ \(\vec{u}=(x;y;z)\) và \(\vec{u'}=(x';y'; z')\):
\(\vec{u}+\vec{u'}=(x+x';y+y';z+ z')\)
\(\vec{u}-\vec{u'}=(x-x';y-y';z- z')\)
\(k\vec{u}=(kx;ky;kz)\)
\(\vec{u}=u'\Leftrightarrow \left\{\begin{matrix} x=x'\\ y=y'\\ z=z' \end{matrix}\right.\)
\(\vec{u}=\vec{u'}\) cùng phương \(\Leftrightarrow \left\{\begin{matrix} x=kx'\\ y=ky'\\ z=kz' \end{matrix}\right.\)
\(\left | \vec{u} \right |=\sqrt{x^2+y^2+z^2}\)
Cho hai điểm \(A(x_A,y_A,z_A)\); \(B(x_B,y_B,z_B)\):
\(\overrightarrow{AB}=(x_B-x_A;y_B-y_A;z_B-z_A)\)
\(AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2}\)
\(\overrightarrow{IA}=k.\overrightarrow{IB}(k\neq 1)\Leftrightarrow \left\{\begin{matrix} x_I=\frac{x_A-k.x_B}{1-k}\\ \\ y_I=\frac{y_A-k.y_B}{1-k}\\ \\ z_I=\frac{z_A-k.z_B}{1-k} \end{matrix}\right.\)
Đặc biệt I là trung điểm AB thì: \(\left\{\begin{matrix} x_I=\frac{x_A+x_B}{2}\\ \\ y_I=\frac{y_A+y_B}{2}\\ \\ z_I=\frac{z_A+z_B}{2} \end{matrix}\right.\)
G là trọng tâm \(\Delta ABC\): \(\left\{\begin{matrix} x_G=\frac{x_A+x_B+x_C}{3}\\ \\ y_G=\frac{y_A+y_B+y_C}{3}\\ \\ z_G=\frac{z_A+z_B+z_C}{3} \end{matrix}\right.\)
G là trọng tâm của tứ diện ABCD: \(\left\{\begin{matrix} x_G=\frac{x_A+x_B+x_C+x_D}{4}\\ \\ y_G=\frac{y_A+y_B+y_C+y_D}{4}\\ \\ z_G=\frac{z_A+z_B+z_C+z_D}{4} \end{matrix}\right.\)
1.3. Tích vô hướng
Công thức tính tích vô hướng: \(\vec{a}.\vec{b}=\left | \vec{a} \right |.\left | \vec{b} \right |.cos(\vec{a},\vec{b})\).
Biểu thức tọa độ của tích vô hướng: \(\left.\begin{matrix} \vec{a}=(x_1;y_1;z_1)\\ \vec{b}=(x_2;y_2;z_2) \end{matrix}\right\} \vec{a}.\vec{b} = x_1.x_2 + y_1.y_2 + z_1.z_2\).
Công thức tính góc giữa hai vectơ: \(cos(\vec a,\vec b) = \frac{{\vec a.\vec b}}{{\left| {\vec a} \right|.\left| {\vec b} \right|}}.\)
1.4. Phương trình mặt cầu
Trong không gian Oxyz, mặt cầu tâm I(a;b;c), bán kính R có phương trình: \((x-a)^2+(y-b)^2+(z-c)^2=R^2.\)
Nhận xét: Phương trình mặt cầu có thể viết dưới dạng \(x^2+y^2+z^2-2Ax-2By-2Cz+D=0\), điều kiện \(A^2+B^2+C^2-D> 0\).
Khi đó, mặt cầu có tâm \(I(A;B;C)\), bán kính \(R = \sqrt {{A^2} + {B^2} + {C^2} - D} .\)
2. Bài tập minh hoạ
2.1. Bài tập 1
Cho A(3;0;4), B(1;2;3), C(9;6;4). Tìm:
a) Trọng tâm tam giác ABC.
b) Tọa độ đỉnh D để ABCD là hình bình hành.
c) Tọa độ giao điểm hai đường chéo của hình bình hành ABCD.
Hướng dẫn giải
a) Gọi G là trọng tâm tam giác ABC, ta có:
\(\left\{ \begin{array}{l} {x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\ {y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\\ {z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} {x_G} = \frac{{13}}{3}\\ {y_G} = \frac{8}{3}\\ {z_G} = \frac{{11}}{3} \end{array} \right.\)
Vậy \(G\left( {\frac{{11}}{3};\frac{8}{3};\frac{{11}}{3}} \right).\)
b) Gọi \(D\left( {{x_D};{y_D};{z_D}} \right)\)
\(\begin{array}{l} \overrightarrow {AB} = ( - 2;2; - 1)\\ \overrightarrow {DC} = (9 - {x_D};6 - {y_D};4 - {z_D}) \end{array}\)
Để ABCD là hình bình hành thì:
\(\overrightarrow {AB} = \overrightarrow {DC}\)
Hay: \(\left\{ \begin{array}{l} - 2 = 9 - {x_D}\\ 2 = 6 - {y_D}\\ - 1 = 4 - {z_D} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} {x_D} = 11\\ {y_D} = 4\\ {z_D} = 5 \end{array} \right. \Rightarrow D(11;4;5)\)
c) Gọi I là giao điểm hai đường chéo AC và BD thì:
I là trung điểm của AC \(\Rightarrow \left\{ \begin{array}{l} {x_I} = \frac{{{x_A} + {x_C}}}{2} = 6\\ {y_I} = \frac{{y{}_A + {y_C}}}{2} = 3\\ {z_I} = \frac{{{z_A} + {z_C}}}{2} = 4 \end{array} \right. \Rightarrow I(6,3,4)\).
2.2. Bài tập 2
Trong mặt phẳng (P) cho hình chóp S.ABC có tọa độ các đỉnh \(A(0;0;0);\,B\left( {\frac{a}{2};\frac{{a\sqrt 3 }}{2};0} \right);C(a;0;0);S(0;0;a)\). Tính góc giữa hai đường thẳng AB và SC.
Hướng dẫn giải
Ta có: \(\overrightarrow {AB} = \left( {\frac{a}{2};\frac{{a\sqrt 3 }}{2};0} \right)\); \(\overrightarrow {SC} = \left( {a;0; - a} \right).\)
\(\cos \left( {AB,SC} \right) = \frac{{\left| {\overrightarrow {AB} .\overrightarrow {SC} } \right|}}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {SC} } \right|}} = \frac{{\sqrt 2 }}{4} \Rightarrow \widehat {\left( {AB,SC} \right)} \approx {69^0}18'.\)
2.3. Bài tập 3
Trong không gian với hệ tọa độ Oxyz, cho điểm A(-1;-1;2) điểm B(-1;-1;0). Viết phương trình mặt cầu đường kính AB.
Hướng dẫn giải
Gọi I là trung điểm AB ta có: \(\left\{ \begin{array}{l} {x_I} = \frac{{{x_A} + {x_B}}}{2} = - 1\\ {y_I} = \frac{{{y_A} + {y_B}}}{2} = - 1\\ {z_I} = \frac{{{z_A} + {z_B}}}{2} = 1 \end{array} \right. \Rightarrow I( - 1; - 1;1)\)
Ta có: \(IA = IB = 1.\)
Mặt cầu đường kính AB, nhận điểm I làm tâm, có bán kính R=IA=1 nên có phương trình là:
\({(x + 1)^2} + {(y + 1)^2} + {(z - 1)^2} = 1.\)
2.4. Bài tập 4
Lập phương trình mặt cầu ngoại tiếp tứ diện ABCD với A(1; 1; 0), B(3; 1; 2), C(-1; 1; 2) và D(1;-1;2).
Hướng dẫn giải
Gọi phương trình mặt cầu là: \(\,{x^2} + {y^2} + {z^2} - 2{\rm{ax}}\,{\rm{ - }}\,{\rm{2by}}\,{\rm{ - }}\,{\rm{2cz}}\,{\rm{ + }}\,{\rm{d}}\,{\rm{ = }}\,{\rm{0}}\,\left( {{{\rm{a}}^{\rm{2}}} + {b^2} + {c^2} - d > 0} \right)\)
Mặt cầu đi qua 4 điểm A, B, C, D nên:
\(\Rightarrow \left\{ \begin{array}{l} -2a - 2b + d + 2 = 0\\ -6a - 2b - 4c + d + 14 = 0\\ 2a - 2b - 4c + d + 6 = 0\\ -2a + 2b - 4c + d + 6 = 0 \end{array} \right.\,\,\,\, \Rightarrow a = b = 1;\,c = 2;d = 2\)
Kết luận: Phương trình mặt cầu là \(x^2+y^2+z^2-2x-2y-4z+2=0.\)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Trong không gian Oxyz cho ba vecto \(\overrightarrow a = (2; - 1;2),\overrightarrow b = (3;0;1),\overrightarrow c = ( - 4;1; - 1)\). Tìm tọa độ của các vecto \(\overrightarrow m \) và \(\overrightarrow n \) biết rằng:
a) \(\overrightarrow m = 3\overrightarrow a - 2\overrightarrow b + \overrightarrow c \)
b) \(\overrightarrow n = 2\overrightarrow a + \overrightarrow b + 4\overrightarrow c \)
Câu 2: Trong không gian Oxyz cho điểm M có tọa độ (x0; y0 ; z0). Tìm tọa độ hình chiếu vuông góc của điểm M trên các mặt phẳng tọa độ (Oxy), (Oyz), (Ozx).
Câu 3: Tìm tâm và bán kính của các mặt cầu có phương trình sau đây:
a) \(\small x^2 + y^2 + z^2 - 8x - 2y + 1 = 0\)
b) \(\small 3x^2 + 3y^2 + 3z^2 - 6x + 8y + 15z - 3 = 0\)
Câu 4: Trong không gian Oxyz, hãy tìm trên mặt phẳng (Oxz) một điểm M cách đều ba điểm A(1; 1; 1), B(-1; 1; 0), C(3; 1; -1).
Câu 5: Cho hình tứ diện ABCD. Chứng minh rằng:
a) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AD} + \overline {BC} \)
b) \(\overrightarrow {AB} = \dfrac{1}{2}\overrightarrow {AC} + \dfrac{1}{2}\overrightarrow {AD} + \dfrac{1}{2}\overrightarrow {CD} + \overrightarrow {DB} \)
3.2. Bài tập trắc nghiệm
Câu 1: Trong không gian Oxyz, cho ba vectơ \(\overrightarrow a = \left( {2; - 1;2} \right),\overrightarrow b = \left( {3;0;1} \right),\overrightarrow c = \left( { - 4;1; - 1} \right)\). Tìm tọa độ \(\overrightarrow m = 3\overrightarrow a - 2\overrightarrow b + \overrightarrow c.\)
A. \(\overrightarrow m = \left( { - 4;2;3} \right)\)
B. \(\overrightarrow m = \left( { - 4;-2;3} \right)\)
C. \(\overrightarrow m = \left( { - 4;-2;-3} \right)\)
D. \(\overrightarrow m = \left( { - 4;2;-3} \right)\)
Câu 2: Trong không gian với hệ tọa độ Oxyz, cho 3 điểm \(A\left( {1;1;3} \right);B\left( {2;3;5} \right);C\left( { - 1;2;6} \right)\). Xác định tọa độ điểm M sao cho \(\overrightarrow {MA} + 2\overrightarrow {MB} - 2\overrightarrow {MC} = 0\).
A. \(M\left( {7;3;1} \right)\)
B. \(M\left( { - 7; - 3; - 1} \right)\)
C. \(M\left( {7; - 3;1} \right)\)
D. \(M\left( {7; - 3; - 1} \right)\)
Câu 3: Cho \(\overrightarrow a = \left( {0;0;1} \right);\,\overrightarrow b = \left( {1;1;0} \right);\,\overrightarrow c = \left( {1;1;1} \right)\). Trong các mệnh đề sau, mệnh đề nào đúng?
A. \(\overrightarrow a .\overrightarrow b = 1\)
B. \(\cos \left( {\overrightarrow b ,\overrightarrow c } \right) = \sqrt {2/3}\)
C. \(\left| {\overrightarrow b } \right| = \left| {\overrightarrow a } \right|.\left| {\overrightarrow c } \right|\)
D. \(\overrightarrow a + \overrightarrow b + \overrightarrow c = \overrightarrow 0\)
Câu 4: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \((S):{x^2} + {y^2} + {z^2} - 2x + 4y - 4z - m = 0\) có bán kính R = 5. Tìm giá trị của m.
A. m = -4
B. m = -16
C. m = 16
D. m = -4
Câu 5: Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt cầu đi qua bốn điểm O, \(A\left( {1;0;0} \right),B\left( {0; - 2;0} \right),C\left( {0;0;4} \right)\)
A. \({x^2} + {y^2} + {z^2} - x + 2y - 4z = 0\)
B. \({x^2} + {y^2} + {z^2} +x - 2y + 4z = 0\)
C. \({x^2} + {y^2} + {z^2} - 2x + 4y - 8z = 0\)
D. \({x^2} + {y^2} + {z^2} +2x -4y +8z = 0\)
4. Kết luận
Qua bài học này giúp các em nắm được một số nội dung như sau:
- Hiểu được định nghĩa của hệ trục tọa độ Oxyz trong không gian và biết xác định tọa độ của 1 điểm, của vectơ các phép trái của nó.
- Biết cách tính tích vô hướng của 2 vectơ, độ dài của véc tơ và khoảng cách giữa hai điểm.
- Viết được phương trình mặt cầu, tìm được tâm và bán kính khi viết phương mặt cầu.
