Toán 12 Ôn tập chương 2: Mặt nón, Mặt trụ, Mặt cầu

Mặt nón, hình nón, khối nón.

Mặt trụ, hình trụ, khối trụ.

Mặt cầu, khối cầu, vị trí tương đối giữa mặt cầu với đường thẳng, mặt phẳng.

a) Công thức tính diện tích và thể tích liên quan đến hình nón, khối nón

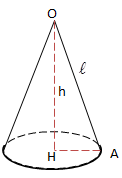
Cho hình nón có đường sinh \(l\), bán kính đáy \(R\), chiều cao \(h\), ta có các công thức sau:

Thể tích khối nón: \(V_{Khoi \, \, non}=\frac{1}{3}.S.h=\frac{1}{3}.\pi .R^{2}.h\).

Diện tích xung quanh hình nón: \(S_{xq}=\pi Rl\).

Diện tích toàn phần hình nón: \(S_{tp}=\pi Rl+\pi R^{2}\).

b) Các công thức tính toán liên quan đển hình trụ, khối trụ

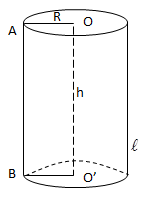
Thể tích khối trụ: \(V=\pi .R^2.h\) (=Sđáy.h).

Diện tích xung quanh hình trụ: \(S_{xq}=2\pi .R.h\).

Diện tích toàn phân hình trụ: \(S_{tp}=2\pi .R.h+2\pi R^2\).

Trong đó:

R: bán kính đáy.

h: chiều cao (k/c giữa hai đáy = OO').​

c) Công thức tính toán liên qua đến mặt cầu, khối cầu

Công thức tính thể tích khối cầu bán kính R: \(V=\frac{4}{3}\pi .R^3\).

Công thức tính diện tích mặt cầu bán kính R: \(S = 4\pi {R^2}.\)

Cho tam giác ABC vuông tại A có AC=3a, AB=4a. Cho tam giác này quay quanh đường thẳng BC, tính thể tích V của khối tròn xoay thu được.

Hướng dẫn giải

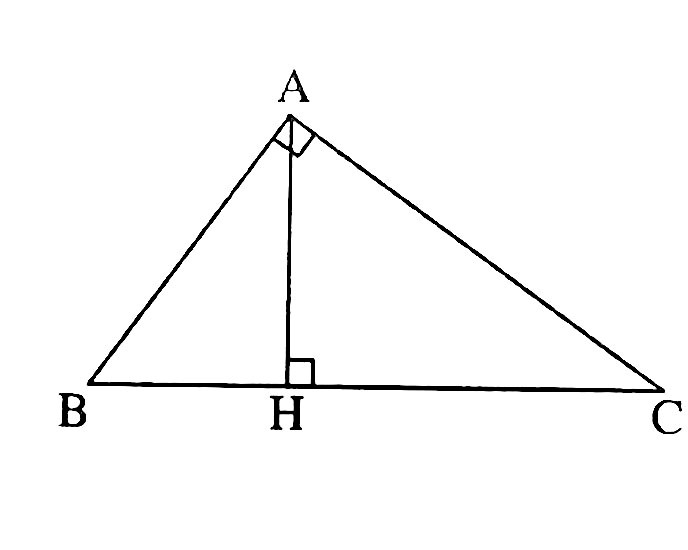
Kẻ đường cao AH của ∆ABC

Khi quay tam giác ABC quanh đường thẳng BC miền tam giác ABC sinh ra hai khối nón chung đáy có bán kính đáy là R = AH và chiều cao lần lượt là HB và HC.

Ta có: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{16{a^2}}} + \frac{1}{{9{a^2}}} = \frac{{25}}{{144{a^2}}}.\)

Suy ra \(A{H^2} = \frac{{25}}{{144{a^2}}}.\)

Mặt khác: \(HB + HC = BC = \sqrt {A{B^2} + A{C^2}} = 5a.\)

Thể tích khối tròn xoay sinh ra là:

\(V = {V_1} + {V_2} = \frac{1}{3}\pi A{H^2}.\left( {HB + HC} \right) = \frac{1}{3}\pi .\frac{{144{a^2}}}{{25}}.5a = \frac{{144\pi {a^2}}}{{15}}.\)

Cho một cái bể nước hình hộp chữ nhật có ba kích thước 2m, 3m, 2m lần lượt là chiều dài, chiều rộng, chiều cao của lòng trong đựng nước của bể. Hàng ngày nước ở trong bể được lấy ra bởi một cái gáo hình trụ có chiều cao là 5 cm bà bán kính đường tròn đáy là 4 cm. Trung bình một ngày được múc ra 170 gáo nước để sử dụng (Biết mỗi lần múc là múc đầy gáo). Hỏi đến ngày thứ bao nhiêu bể sẽ hết nước?

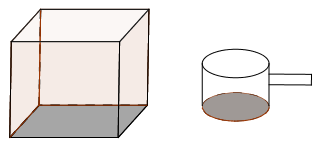
Hướng dẫn giải

Thể tích nước được đựng đầy trong hình bể là là thể tích của hình hộp chữ nhật: \(V = 2.3.2 = 12\left( {{m^3}} \right).\)

Thể tích nước đựng đầy trong một gáo là: \({V_g} = \pi {4^2}.5 = 80\pi \left( {c{m^3}} \right) = \frac{\pi }{{12500}}\left( {{m^3}} \right).\)

Mội ngày bể được múc ra 170 gáo nước tức trong một ngày lượng được được lấy ra là: \({V_m} = 170.{V_g} = \frac{{17}}{{1250}}\pi \left( {{m^3}} \right)\).

Ta có: \(\frac{V}{{{V_m}}} = \frac{{12}}{{\frac{{17}}{{1250}}\pi }} \simeq 280,8616643\)

Vậy đến ngày thứ 281 bể sẽ hết nước.

Một quả bóng bàn và một chiếc chén hình trụ có cùng chiều cao. Người ta đặt quả bóng lên chiếc chén thấy phần ở ngoài của quả bóng có chiều cao bằng \(\frac{3}{4}\) chiều cao của nó. Tìm V1, V2 lần lượt là thể tích của quả bóng và chiếc chén. 

Hướng dẫn giải

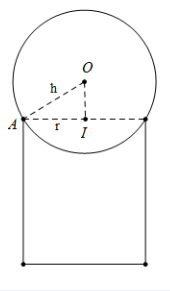
Gọi chiều cao của chiếc chén hình trụ là 2h và bán kính đường tròn đáy của hình trụ là r.

Gọi O là tâm của quả bóng bàn, khi đó khoảng cách từ O đến mặt phẳng thiết diện bằng \(\frac{h}{2}\) 

Bán kính đường tròn đáy hình trụ là \(AI = \sqrt {O{A^2} - O{I^2}} = \frac{{h\sqrt 3 }}{2}.\)

Thể tích của quả bóng bàn là  \({V_1} = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {h^3} = \frac{{4\pi {h^3}}}{3}.\)

Thể tích của chiếc chén là: \({V_2} = \pi {r^2}{h_c} = \pi {\left( {\frac{{h\sqrt 3 }}{2}} \right)^2}.2h = \frac{{3\pi {h^3}}}{2}.\) 

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, BC=2a. SA vuông góc (ABC) và \(SA = 2a\sqrt 2\). Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.

Hướng dẫn giải

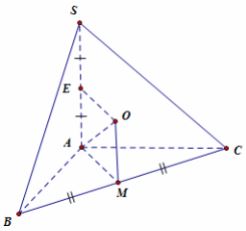
Gọi M là trung điểm của BC.

Do ABC là tam giác vuông cân tại A nên: \(AB = AC = \frac{{BC}}{{\sqrt 2 }} = a\sqrt 2 ;AM = \frac{{BC}}{2} = a\)  

Dựng đường thẳng qua M song song với SA và cắt mặt phẳng trung trực của SA tại 0.

Khi đó O là tâm mặt cầu ngoại tiếp hình chóp.

Do ABCD là hình chữ nhật nên: \(OM=AE=a \sqrt 2.\)

Mặc khác: \(R = OA = \sqrt {O{M^2} + M{A^2}} = \sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {a^2}} = a\sqrt 3\)

Vậy thể tích khối cầu ngoại tiếp hình chóp là: \(V = \frac{4}{3}\pi {R^3} = 4\pi {a^3}\sqrt 3 .\)

Câu 1: Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC) và cạnh BD vuông góc với cạnh BC. Biết AB = AD = a. Tính diện tích xung quanh của hình nón và thể tích của khối nón được tạo thành khi quay đường gấp khúc BDA quanh cạnh AB.

Câu 2: Một hình chóp có tất cả các cạnh bên bằng nhau. Chứng minh rằng hình chóp đó nội tiếp được trong một mặt cầu (các đỉnh của hình chóp nằm trên mặt cầu).

Câu 3: Hình chóp S.ABC có một mặt cầu tiếp xúc với các cạnh bên SA, SB, SC. Mặt cầu này còn tiếp xúc với ba cạnh AB, BC, CA tại trung điểm của mỗi cạnh. Chứng minh rằng hình chóp đó là hình chóp tam giác đều.

Câu 4: Cho tứ diện đều ABCD cạnh a. Gọi H là hình chiếu vuông góc của đỉnh A xuống mặt phẳng (BCD).

a) Chứng minh H là tâm đường tròn ngoại tiếp tam giác BCD. Tính độ dài đoạn AH.

b) Tính diện tích xung quanh của hình trụ và thể tích của khối trụ có đường tròn đáy ngoại tiếp tam giác BCD và chiều cao AH.

Câu 5: Cho hình vuông ABCD cạnh a. Từ tâm O của hình vuông dựng đường thẳng ∆ vuông góc với mặt phẳng (ABCD). Trên ∆ lấy điểm S sao cho OS = a/2 . Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABCD. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó.

Câu 1: Cho tam giác ABC đều cạnh a, đường cao AH. Tính thể tích V của khối nón sinh ra khi cho tam giác ABC quay xung quanh trục AH.

A. \(V = \frac{{\pi {a^3}\sqrt 6 }}{{12}}\)

B. \(V = \frac{{\pi {a^3}\sqrt 3 }}{{12}}\)

C. \(V = \frac{{\pi {a^3}\sqrt 2 }}{{24}}\)

D. \(V = \frac{{\pi {a^3}\sqrt 3 }}{{24}}\)

Câu 2: Hình nón có thiết diện qua trục là tam giác đều. Tính độ dài đường cao h của hình nón.

A. \(h = \frac{a}{4}.\)  

B. \(h = \frac{{\sqrt 3 }}{4}a.\)

C. \(h = \frac{a}{2}.\)

D. \(h = \frac{{\sqrt 3 }}{2}a.\)

Câu 3: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông cạnh a và cạnh bên bằng 2a. Tính diện tích xung quanh \(S_{xq}\) của hình nón có đỉnh là tâm O của hình vuông A’B’C’D’ và đáy là hình tròn nội tiếp hình vuông ABCD.​

A. \(S_{xq}=\frac{{\pi {a^2}\sqrt {17} }}{4}\)  

B. \({S_{xq}} = \pi {a^2}\) 

C. \({S_{xq}} = \frac{{\pi {a^2}\sqrt {17} }}{2}\)  

D. \({S_{xq}} = \pi {a^2}\sqrt {17}\)

Câu 4: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có độ dài đáy bằng 3a và chiều cao bằng h. Tính thể tích V của khối trụ ngoại tiếp lăng trụ đã cho.

A. \(\pi {a^2}h\) 

B. \(3\pi {a^2}h\) 

C.  \(27\pi {a^2}h\) 

D. \(9\pi {a^2}h\)

Câu 5: Gọi \(V_1\) là thể tích giữa khối lập phương và \(V_2\) là thể tích khối cầu ngoại tiếp khối lập phương đó. Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}.\)

A. \(\frac{{{V_1}}}{{{V_2}}} = \frac{{3\pi }}{{2\sqrt 3 }}.\)

B. \(\frac{{{V_1}}}{{{V_2}}} = \frac{{\pi \sqrt 2 }}{3}.\)

C. \(\frac{{{V_1}}}{{{V_2}}} = \frac{3}{{\pi \sqrt 2 }}.\)

D. \(\frac{{{V_1}}}{{{V_2}}} = \frac{{2\sqrt 3 }}{{3\pi }}.\)

Qua bài này học sinh nắm được các nội dung chính như sau:

•  Nắm được thế nào là hình tròn xoay , mặt tròn xoay và sự hình thành hình tròn xoay, mặt tròn xoay, đường sinh trục.
•  Nắm vững định nghĩa mặt nón tròn xoay, khối nón tròn xoay. Công thức tínhdiện tích mặt nón và công thức tính thể tich khối nón.
•  Nhận biết được một hình cho trước là hình tròn xoay hay không tròn xoay.
•  Liên hệ được sự hình thành các hình tròn xoay trong thực tế.
•  Biết cách tính diện tích và thể tích mặt , vật hình nón.