Toán 12 Chương 1 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị hàm số
Qua bài học các em sẽ nắm được hình dạng cũng như bước để khảo sát sự biến thiên và vẽ đồ thị hàm số các hàm số phổ biến trong chương trình phổ thông như hàm số bậc ba, hàm số bậc bốn trùng phương và hàm số phân thức bậc nhất/ bậc nhất (hàm nhất biến).
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Các bước khảo sát và vẽ đồ thị hàm số y = f(x)
- Bước 1: Tìm tập xác định của hàm số
- Bước 2: Tính đạo hàm y' = f'(x), tìm nghiệm của phương trình
- Bước 3: Tính giới hạn \(\mathop {\lim }\limits_{x \to + \infty } y,\mathop {\lim }\limits_{x \to - \infty } y\) và tìm tiệm cận đứng, ngang (nếu có)
- Bước 4: Lập bảng biến thiên
- Bước 5: Kết luận tính biến thiên và cực trị (nếu có)
- Bước 6: Nêu tâm đối xứng, trục đối xứng (nếu có).
- Bước 7: Tìm các điểm đặc biệt của đồ thị (giao với trục Ox, Oy, các điểm đối xứng, ...)
- Bước 8: Vẽ đồ thị.
1.2. Chú ý
- Đồ thị hàm số bậc ba nhận điểm \(I(x_0,f(x_0))\) với \(x_0\) là nghiệm phương trình \(f''(x_0)=0\) làm tâm đối xứng.
- Đồ thị hàm số phân thức bậc nhất/bậc nhất nhận giao của hai tiệm cận làm tâm đối xứng.
- Đồ thị hàm số lẻ nhận \(O(0;0)\) làm tâm đối xứng.
- Đồ thị hàm số chẵn nhận Oy làm trục đối xứng.
1.3. Các dạng đồ thị của hàm số bậc 3 y= ax3 + bx2 + cx + d (a ≠ 0)
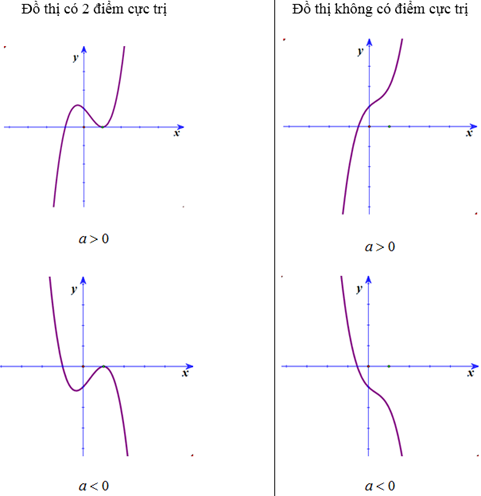
- Lưu ý: Đồ thị hàm số có 2 điểm cực trị nằm 2 phía so với trục Oy khi ac < 0
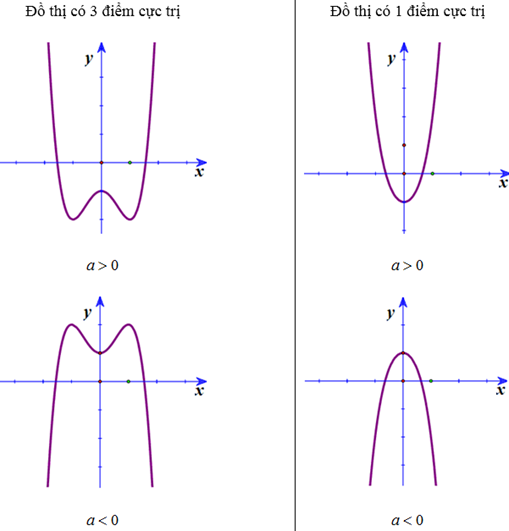
1.4. Các dạng đồ thị của hàm số bậc 4 trùng phương y = ax4 + bx2 + c (a ≠ 0)
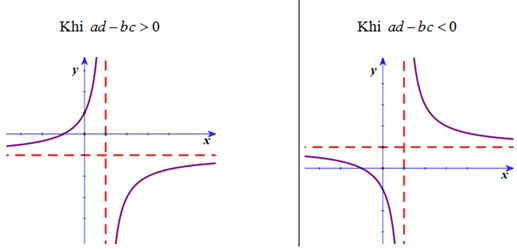
1.5. Các dạng đồ thị của hàm số nhất biến \(y = \frac{{ax + b}}{{cx + d}}\) (ab - bc ≠ 0)
1.6. Biến đổi đồ thị
Cho hàm số y = f(x) có đồ thị (C). Khi đó, với số a > 0 ta có:
• Hàm số y = f(x) + a có đồ thị (C') là tịnh tiến (C) theo phương của Oy lên trên a đơn vị.
• Hàm số y = f(x) - a có đồ thị (C') là tịnh tiến (C) theo phương của Oy xuống dưới a đơn vị.
• Hàm số y = f(x + a) có đồ thị (C') là tịnh tiến (C) theo phương của Ox qua trái a đơn vị.
• Hàm số y = f(x - a) có đồ thị (C') là tịnh tiến (C) theo phương của Ox qua phải a đơn vị.
• Hàm số y = -f(x) có đồ thị (C') là đối xứng của (C) qua trục Ox.
• Hàm số y = f(-x) có đồ thị (C') là đối xứng của (C) qua trục Oy.
• Hàm số \(y = f\left( {\left| x \right|} \right) = \left\{ \begin{array}{l}
f\left( x \right)\;\;\;\;\;\;\;khi\;\;\;\;x > 0\\
f\left( { - x} \right)\;\;\;\;khi\;\;\;\;x \le 0
\end{array} \right.\) có đồ thị (C') bằng cách
- Giữ nguyên phần đồ thị (C) nằm bên phải trục Oy và bỏ phần (C) nằm bên trái Oy.
- Lấy đối xứng phần đồ thị (C) nằm bên phải trục Oy qua Oy.
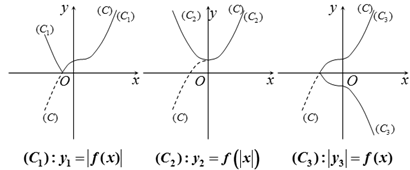
• Hàm số \(y = \left| {f\left( x \right)} \right| = \left\{ \begin{array}{l}
f\left( x \right)\;\;\;\;\;\;\;khi\;\;\;\;f\left( x \right) > 0\\
- f\left( x \right)\;\;\;\;khi\;\;\;\;f\left( x \right) \le 0
\end{array} \right.\) có đồ thị (C') bằng cách:
- Giữ nguyên phần đồ thị (C) nằm trên Ox.
- Lấy đối xứng phần đồ thị (C) nằm dưới Ox qua Ox và bỏ phần đồ thị (C) nằm dưới Ox.
2. Bài tập minh hoạ
2.1. Dạng 1: Khảo sát hàm số bậc 3
Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\).
Hướng dẫn giải
+ Bước 1: Tập xác định: \(D=\mathbb{R}.\)
+ Bước 2: \(y'=3x^2-6x\)
\(y' = 0 \Leftrightarrow 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 2 \end{array} \right.\)
+ Bước 3: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\mathop {\lim }\limits_{x \to + \infty } y = + \infty\)
+ Bước 4: Bảng biến thiên
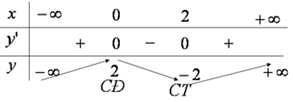
+ Bước 5: Vậy
Hàm số đồng biến trên \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\).
Hàm số nghịch biến trên \((0;2).\)
Hàm số đạt cực đại tại x=0; giá trị cực đại là y=2.
Hàm số đạt cực tiểu tại x=2; giá trị cực tiểu là y=-2.
+ Bước 6: \(y''=6x-6\)
\(y'' = 0 \Leftrightarrow 6x - 6 = 0 \Leftrightarrow x = 1 \Rightarrow y = 0\)
Vậy đồ thị hàm số nhận điểm I(1;0) làm tâm đối xứng.
+ Bước 7: Cho: \(x = - 1 \Rightarrow y = - 2;x = 3 \Rightarrow y = 2\)
+ Bước 8: Đồ thị hàm số
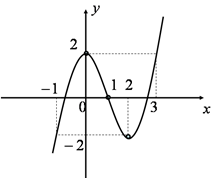
2.2. Dạng 2: Khảo sát hàm số trùng phương
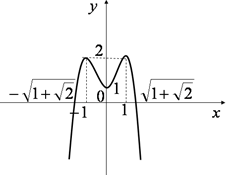
Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y = - {x^4} + 2{x^2} + 1\).
Hướng dẫn giải
+ Bước 1: Tập xác định: \(D=\mathbb{R}.\)
+ Bước 2: \(y' = - 4{x^3} + 4x\)
\(y' = 0 \Leftrightarrow - 4{x^3} + 4x = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ {x^2} = 1 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = \pm 1 \end{array} \right.\)
+ Bước 3: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\mathop {\lim }\limits_{x \to + \infty } y = - \infty\)
+ Bước 4: Bảng biến thiên:
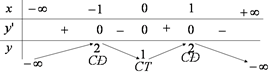
+ Bước 5: Vậy
Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right).\)
Hàm số nghịch biến trên các khoảng \((-1;0)\) và \(\left( {1; + \infty } \right)\).
Hàm số đạt cực đại tại x=-1 và x=1; giá trị cực đại y=2.
Hàm số đạt cực tiểu tại x=0; giá trị cực tiểu y=1.
+ Bước 6: Đồ thị hàm số nhậc trục Oy là trục đối xứng.
+ Bước 7: \(\begin{array}{l} y = 0 \Leftrightarrow - {x^4} + 2{x^2} + 1 = 0\\ \Rightarrow \left[ \begin{array}{l} {x^2} = 1 + \sqrt 2 \\ {x^2} = 1 - \sqrt 2 (L) \end{array} \right. \Rightarrow x = \pm \sqrt {1 + \sqrt 2 } \end{array}.\)
+ Bước 8: Đồ thị hàm số:
2.3. Dạng 3: Khảo sát hàm số nhất biến
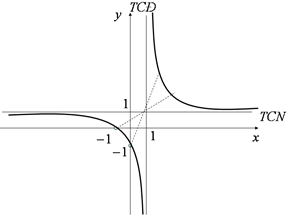
Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y = \frac{{x + 1}}{{x - 1}}\)
Hướng dẫn giải
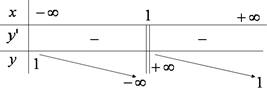
+ Bước 1: Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\)
+ Bước 2: \(y' = \frac{{ - 2}}{{{{(x - 1)}^2}}} < 0\)
+ Bước 3: Vậy
Hàm số đồng biến trên các khoảng \((-\infty ;1);(1;+\infty )\).
Hàm số không có cực trị.
+ Bước 4: Ta có:
\(\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty\); \(\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty\) nên đồ thị hàm số nhận đường thẳng x=1 làm tiệm cận đứng.
\(\mathop {\lim }\limits_{x \to + \infty } y = 1\) ; \(\mathop {\lim }\limits_{x \to - \infty } y = 1\) nên đồ thị hàm số nhận đường thẳng y=1 làm tiệm cận ngang.
+ Bước 5: Bảng biến thiên:
+ Bước 6: Đồ thị hàm số nhận điểm I(1;1) là tâm đối xứng.
+ Bước 7: Cho: \(x = 0 \Rightarrow y = - 1;y = 0 \Rightarrow x = - 1\).
+ Bước 8: Đồ thị hàm số:
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc ba sau:
a) \(y=2+3x-{{x}^{3}}\)
b) \(y={{x}^{3}}+4{{x}^{2}}+4x\)
Câu 2: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc bốn sau:
a) \(y=-{{x}^{4}}+8{{x}^{2}}-1\)
b) \(y={{x}^{4}}-2{{x}^{2}}+2\)
Câu 3: Khảo sát và vẽ đồ thị các hàm số:
a) \(y=2-3x-x^2\)
b) \(y=x^3-x^2+x\)
c) \(y=-x^4+2x^3+3\)
Câu 4: Khảo sát và vẽ đồ thị các hàm số :
a) \(y=\dfrac{x-2}{x+1}\)
b) \(y=\dfrac{2-x}{2x-1}\)
Câu 5: Tìm giá trị của tham số m để hàm số
\(y=(m-1)x^4-mx^2+3\) có đúng một cực trị
3.2. Bài tập trắc nghiệm
Câu 1: Cho hàm số y= f(x) có \(\mathop {\lim }\limits_{x \to + \infty } f(x) = 0\) và
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = + \infty .\) Mệnh đề nào sau đây đúng?
A. Đồ thị của hàm số y = f(x) không có tiệm cận ngang.
B. Đồ thị của hàm số y = f(x) có một tiệm cận đứng là đường thẳng y = 0.
C. Đồ thị của hàm số y = f(x) nằm phía trên trục hoành
D.Đồ thị của hàm số y = f(x) có một tiệm cận ngang là trục hoành.
Câu 2: Đường cong ở hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê trong bốn phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào?
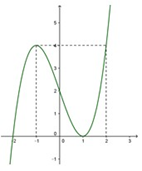
A. \(y = - {x^3} + 3x + 2\)
B. \(y = {x^3} + 3x + 2\)
C. \(y = {x^3} - 3x + 2\)
D. \(y = - {x^3} - 3x + 2\)
Câu 3: Hàm số \(y=x^3+(m+3)x^2+mx-2\) đạt cực tiểu tại \(x=1\). Khi :
A. \(m=1\)
B. \(m=2\)
C. \(m=-3\)
D. \(m=4\)
Câu 4: Hàm số \(y=x^4+(m^2-4)x^2+5\) có ba cực trị khi :
A. \(-2 < m < 2\)
B. \(m=2\)
C. \(m < -2\)
D. \(m > 2\)
Câu 5: Phương trình tiếp tuyến của đồ thị hàm số \(y=x^4-2x^2\) tại điểm có hoành độ \(x=-2\) là :
A. \(y=-24x+40\)
B. \( y=24 x-40\)
C. \(y=-24x-40\)
D. \(y=-24 x\)
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Khảo sát sự biến thiên và vẽ đồ thị hàm số Toán 12 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài học giúp học sinh
- Biết sơ đồ tổng quát để khảo sát hàm số: tìm tập xác định, xét chiều biến thiên, tìm cực trị, tìm tiệm cận, lập bảng biến thiên và vẽ đồ thị hàm số.
- Biết cách phân loại các dạng đồ thị hàm số.
Tham khảo thêm
- docx Toán 12 Chương 1 Bài 1: Sự đồng biến, nghịch biến của hàm số
- docx Toán 12 Chương 1 Bài 2: Cực trị của hàm số
- docx Toán 12 Chương 1 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- docx Toán 12 Chương 1 Bài 4: Đường tiệm cận
- docx Toán 12 Ôn tập chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
