Toán 12 Chương 3 Bài 3: Ứng dụng của tích phân trong hình học

Nếu hàm số \(y=f(x)\) liên tục trên \([a;b]\) thì diện tích S của hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a,x=b\) là \(S = \int\limits_a^b {\left| {f(x)} \right|dx} .\)

Diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y = f(x)\), \(y = g(x)\) và hai đường thẳng \(x=a,x=b\) là: \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx}\)

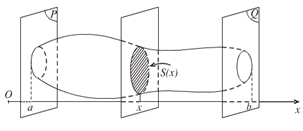
Thể tích vật thể B giới hạn bởi  hai mặt phẳng vuông góc với trục Ox tại các điểm \(a,b\) là \(V = \int\limits_a^b {S(x)dx}.\) Trong đó S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là \(x \in \left[ {a;\,b} \right]\) và S(x) là một hàm liên tục.

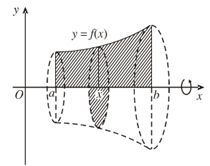
Hàm số  \(y=f(x)\) liên tục và không âm trên \([a,b].\) Hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a,x=b\) quay quanh trục hoành tạo nên một khối tròn xoay. Thể tích V được tính bởi công thức \(V = \pi \int\limits_a^b {{f^2}(x)dx} .\) 

Cho hai hàm số  \(y=f(x)\), \(y=g(x)\) thỏa \(0\leq g(x)\leq f(x)\), liên tục và không âm trên \([a,b].\) Hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), \(y=g(x)\) và hai đường thẳng \(x=a,x=b\) quay quanh trục hoành tạo nên một khối tròn xoay. Thể tích V được tính bởi công thức \(V = \pi \int\limits_a^b {\left[ {{f^2}(x) - {g^2}(x)} \right]dx}.\)

Cho hai hàm số hình phẳng giới hạn bởi đồ thị hàm số  \(y=f(x)\) và \(y=g(x)\)​ quay quanh trục hoành hoành tạo nên một khối tròn xoay. Để tính được thể tích khối tròn xoay ta thực hiện các bước:

Giải phương trình \(f(x) = g(x) \Leftrightarrow \left[ \begin{array}{l} x = a\\ x = b \end{array} \right.\) (Thường dạng bài này đề bài cho phương trình hoành độ giao điểm có hai nghiệm phân biệt).

Giải sử \(0\leq g(x)\leq f(x)\) với mọi x thuộc \([a,b].\) Khi đó: \(V = \pi \int\limits_a^b {\left[ {{f^2}(x) - {g^2}(x)} \right]dx}.\)

Hình phẳng giới hạn bởi đồ thị hàm số \(x = g(y)\), trục tung và hai đường thẳng \(y = c,\,y = d\) quay quanh trục tung tạo nên một khối tròn xoay. Thể tích V được tính bởi công thức \(V = \pi \int\limits_c^d {{g^2}(y)dy}.\)

Câu 1: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \left( {e + 1} \right)x\) và \(y=(1+e^x)x.\)

Hướng dẫn giải

Phương trình hoành độ giao điểm của hai đường cong là:\(\left( {e + 1} \right)x = \left( {1 + {e^x}} \right)x \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0}\\ {{e^x} = e} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0}\\ {x = 1} \end{array}} \right.\) 

Nhận xét, với \(x \in \left[ {0;1} \right]\) thì hiệu số \(\left( {1 + {e^x}} \right)x - \left( {e + 1} \right)x = x\left( {{e^x} - e} \right) > 0.\) 

Khi đó, diện tích hình phẳng cần tìm là \(S = \int\limits_0^1 {\left| {\left( {1 + {e^x}} \right)x - \left( {e + 1} \right)x} \right|} dx = \int\limits_0^1 {\left| {x\left( {{e^x} - e} \right)} \right|dx = \int\limits_0^1 {x\left( {{e^x} - e} \right)} dx}\) 

Đặt \(\left\{ {\begin{array}{*{20}{c}} {u = x}\\ {dv = \left( {e - {e^x}} \right)dx} \end{array} \Rightarrow \left\{ {\begin{array}{*{20}{c}} {du = dx}\\ {v = ex - {e^x}} \end{array}} \right.} \right.\)

\({ \Rightarrow S = x\left( {ex - {e^x}} \right)\left| {_0^1} \right. - \int\limits_0^1 {\left( {ex - {e^x}} \right)dx} }\) \(= \left( { - \frac{{e{x^2}}}{2} + {e^x}} \right)\left| {\begin{array}{*{20}{c}} 1\\ 0 \end{array}} \right. = \frac{{e - 2}}{2}.\)

Câu 2: Tính diện tích tích hình phẳng giới hạn bởi các đường cong \(y = {x^3},\) trục hoành và hai đường thẳng \(x = - 1,x = 2.\)

Hướng dẫn giải

Phương trình hoành độ giao điểm của đường cong \(y = {x^3}\) và trục hoành: 

Diện tích hình phẳng cần tính:

\(S = \int\limits_{ - 1}^0 {\left| {{x^3}} \right|dx + \int\limits_0^2 {\left| {{x^3}} \right|dx} = \int\limits_{ - 1}^0 {\left( { - {x^3}} \right)} dx + \int\limits_0^2 {{x^3}dx} }\) \(= \left. { - \frac{{{x^4}}}{4}} \right|_{ - 1}^0 + \left. {\frac{{{x^4}}}{4}} \right|_0^2 = \frac{{17}}{4}\)

Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng \(x=0\) và \(x=3\) , có thiết diện bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\left( {0 \le x \le 3} \right)\) là một hình chữ nhật có hai kích thước bằng \(x\) và \(2\sqrt {9 - {x^2}}.\)

Hướng dẫn giải

Diện tích của hình chữ nhật có hai cạnh là \(x;2\sqrt {9 - {x^2}}\) là \(2x\sqrt {9 - {x^2}}\) 

Khi đó, thể tích của vật thể được xác định bằng công thức \(V = \int\limits_0^3 {2x\sqrt {9 - {x^2}} dx}\) 

Đặt \(t = \sqrt {9 - {x^2}} \Leftrightarrow {t^2} = 9 - {x^2} \Leftrightarrow xdx = - tdt\) và \(\left\{ {\begin{array}{*{20}{c}} {x = 0 \Rightarrow t = 3}\\ {x = 3 \Rightarrow t = 0} \end{array}} \right.\) 

Suy ra \(V = - 2\int\limits_3^0 {{t^2}dt} = \frac{{2{t^3}}}{3}\left| {\begin{array}{*{20}{c}} 3\\ 0 \end{array}} \right. = 18.\) 

Tính thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số \(y = 2x - {x^2}\) và \(y = x\) quay quanh trục Ox.

Hướng dẫn giải

Phương trình hoành độ giao điểm của đồ thị hàm số \(y = 2x - {x^2}\) và đường thẳng \(y=x\) là \(2x - {x^2} = x \Leftrightarrow {x^2} - x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0}\\ {x = 1} \end{array}} \right.\) 

Khi đó, thể tích khối tròn xoay cần tìm là \(V = \pi \int\limits_0^1 {\left| {{{\left( {2x - {x^2}} \right)}^2} - {x^2}} \right|dx} = \pi \int\limits_0^1 {\left| {{x^4} - 4{x^3} + 3{x^2}} \right|dx}\)

\(\Rightarrow V = \left| {\pi \int\limits_0^1 {\left( {{x^4} - 4{x^3} + 3{x^2}} \right)dx} } \right| = \pi \left| {\left( {\frac{{{x^5}}}{5} - {x^4} + {x^3}} \right)\left| {\begin{array}{*{20}{c}} 1\\ 0 \end{array}} \right.} \right| = \frac{\pi }{5}.\)

Câu 1: Tính diện tích hình phẳng giới hạn bởi các đường:

a) \(y = x^2, y = x + 2\)

b) \(y = |lnx|, y = 1\)

c) \(y = (x - 6)^2, y = 6x- x^2\)

Câu 2: Parabol \(y=\frac{x^{2}}{2}\) chia hình tròn có tâm tại gốc tọa độ, bán kính \(2 \sqrt {2}\) thành hai phần. Tìm tỉ số diện tích của chúng

Câu 3: Tính diện tích hình phẳng giới hạn bởi các đường sau:

a) \(y= 2 x - x^2, x+y=2\)

b) \(y=x^3-12 x, y=x^2\)

c) \(x+y=1, x+y=-1, x-y=1, x-y=-1\)

d) \(y=\dfrac{1}{1+x^2}, y=\dfrac{1}{2}\)

Câu 4: Tính thể tích vật thể:

a) Có đáy là một tam giác cho bởi \(y=x, y=0,x=1\). Mỗi thiết diện vuông góc với trục Ox là một hình vuông.

b) Có đáy là một hình tròn giới hạn bởi \(x^2+y^2=1\). Mỗi thiết diện vuông góc với trục Ox là một hình vuông.

Câu 5: Tính thể tích các khối tròn xoay khi quay hình phẳng xác định bởi

a) \(y=2-x^2, y=1\), quay quanh trục Ox.

b) \(y=2x-x^2, y=x\), quay quanh trục Ox.

c) \(y=(2x+1)^\frac{1}{3}, x=0, y=3\)quay quanh trục Oy.

Câu 1: Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số  \(y = {x^4} - 5{x^2} + 4\), trục hoành và hai đường thẳng \(x = 0;x = 1\).

A. \(S = \frac{7}{3}\)

B. \(S = \frac{8}{5}\)

C. \(S = \frac{{38}}{{15}}\)

D. \(S = \frac{{64}}{{25}}\)

Câu 2: Tính thể tích của vật thể nằm giữa hai mặt phẳng \(x = 0;x = \pi\), biết rằng thiết diện của vật thể với mặt phẳng vuông góc với trục Ox tại điểm có hoành độ \(x\left( {0 \le x \le \pi } \right)\) là một tam giác đều có cạnh là \(2\sqrt {\sin x}\).

A. \(\sqrt 3\)

B. \(\frac{\pi }{{\sqrt 3 }}\)

C. \(2\sqrt 3\)

D. \(2\pi\)

Câu 3: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(x^3 - x\) và đồ thị hàm số \(y = x - x^2\)

A. \(\frac{9}{4}\)

B. \(\frac{{37}}{{12}}\)

C. \(\frac{{81}}{{12}}\)

D. 13

Câu 4: Diện tích hình phẳng giới hạn bởi \(y = x^2 - x + 3\) và \(y = 2x + 1\) là:

A. \(\frac{3}{2}\)

B. \(-\frac{3}{2}\)

C. \(\frac{1}{6}\)

D. \(-\frac{1}{6}\)

Câu 5: Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = \sqrt x \) và \(y = 6 - x\) và trục tung là:

A. \(\frac{{16}}{3}\)

B. \(\frac{{11}}{3}\)

C. \(\frac{{19}}{3}\)

D. \(\frac{{32}}{3}\)

Qua bài học này, các em học sinh nắm được một số nội dung chính như sau:

• Nắm được công thức thể tích của một vật thể, công thức thể tích khối tròn xoay, công thức của khối nón, khối nón cụt, khối trụ tròn xoay trong trường hợp vật thể quay xung quanh trục Ox.
• Áp dụng được công thức tính diện tích hình phẳng, thiết lập được công thức tính thể tích khối chóp, khối nón và khối nón cụt.
• Ứng dụng được tích phân để tính được thể tích nói chung và thể tích khối tròn xoay nói riêng.