Toán 12 Chương 2 Bài 1: Khái niệm về mặt tròn xoay

a) Mặt nón

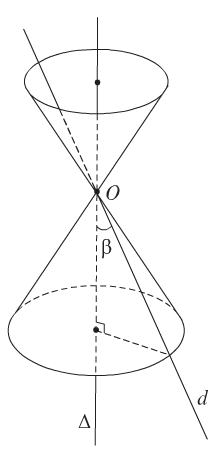
Trong không gian cho hai đường thẳng \(\Delta\) và \(l\) cắt nhau tại O sao cho \((\widehat{\Delta ,l})=\alpha \, (0^{\circ}< \alpha < 90^{\circ}).\)

Cho \(l\) quay quanh \(\Delta\) ta được mặt nón tròn xoay có:

là đường sinh.

\(\Delta\) trục của mặt nón.

\(O=l\cap \Delta\) đỉnh của mặt nón.

\(2\alpha :\) góc ở đỉnh.

b) Hình nón

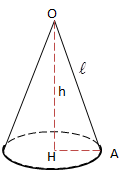
Cắt mặt nón tròn xoay đỉnh O, trục \(\Delta\) bởi mặt phẳng (P) sao cho \((P)\perp \Delta ,O\notin (P).\) 

Hình giới hạn bởi mặt nón, mặt phẳng (P) được gọi là hình nón.

c) Khối nón

Khối nón tròn xoay là phần không gian giới hạn bởi hình nón tròn xoay kể cả hình nón đó.

d) Công thức tính diện tích và thể tích liên quan đến hình nón, khối nón

Cho hình nón có đường sinh \(l\), bán kính đáy \(R\), chiều cao \(h\), ta có các công thức sau:

Thể tích khối nón: \(V_{Khoi \, \, non}=\frac{1}{3}.S.h=\frac{1}{3}.\pi .R^{2}.h\).

Diện tích xung quanh hình nón: \(S_{xq}=\pi Rl\).

Diện tích toàn phần hình nón: \(S_{tp}=\pi Rl+\pi R^{2}\).

a) Mặt trụ

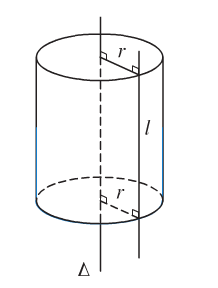
Trong không gian, cho đường thẳng \(l\) song song và cách đường thẳng \(\Delta\) một khoảng R.

Cho \(l\) quay quanh \(\Delta\) ta được một mặt tròn xoay được gọi là mặt trụ tròn xoay có:

\(l\) là đường sinh.

\(\Delta\) là trục mặt trụ

R là bán kính mặt trụ

b) Hình trụ

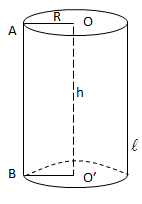
Xét hình chữ nhật OABO'

Cho đường gấp khúc OABO' quay quanh OO' ta được hình trụ tròn xoay:

OA: Bán kính đường tròn đáy.

AB: đường sinh.

c) Khối trụ

Khối trụ tròn xoay là phần không gian giới hạn bởi hình trụ tròn xoay kể cả hình trụ đó.

d) Các công thức tính toán liên quan đển hình trụ, khối trụ

Thể tích khối trụ: \(V=\pi .R^2.h\) (=Sđáy.h).

Diện tích xung quanh hình trụ: \(S_{xq}=2\pi .R.h\).

Diện tích toàn phân hình trụ: \(S_{tp}=2\pi .R.h+2\pi R^2\).

Trong đó:

R: bán kính đáy.

h: chiều cao (k/c giữa hai đáy = OO').​

Câu 1: Trong không gian cho tam giác ABC vuông tại A có AB=a, AC = 2a. Quay tam giác ABC xung quanh cạnh AB ta được một khối nón. Tính thể tích V của khối nón đó.

Hướng dẫn giải

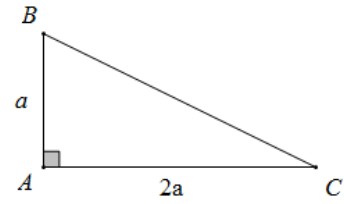
Hình nón thu được có bán kính đáy R=AC=2a, chiều cao h=AB=a.

Vậy thể tích khối nón là: \(V = \frac{1}{3}\pi {r^2}h = \frac{{4\pi {a^3}}}{3}.\)

Câu 2: Trong không gian cho tam giác ABC vuông tại A có có AB=5, AC=12. Cho đường gấp khúc BAC quay quanh cạnh BC ta được hình nón tròn xoay. Tính thể tích của khối nón đó.

Hướng dẫn giải

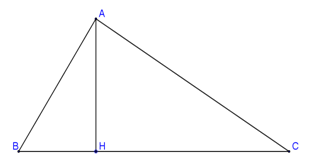
Khi quay đường gấp khúc BAC quay quanh cạnh BC ta được hai hình nón:

Hình nón thứ nhất có đường cao \({h_1} = BH\), Bán kính đáy \({R_1} = AH\).

Hình nón thứ hau có đường cao \({h_2} = CH\), Bán kính đáy \({R_2} = AH\).

Ta có: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{{60}}{{13}}\)

\(BC = \sqrt {A{B^2} + A{C^2}} = 13\)

Vậy thể tích khối tròn xoay thu được là: \(V = \frac{1}{3}\pi {R_1}^2{h_1} + \frac{1}{3}\pi R_2^2{h_2} = \frac{1}{3}\pi A{H^2}(BH + CH) = \frac{{1200}}{{13}}\pi .\)

Câu 3: Thiết diện qua trục của một hình nón là một tam giác vuông có cạnh góc vuông bằng a.

a) Tính diện tích xung quanh và diện tích toàn phần của hình nón.

b) Tính thể tích của khối nó.

c) Một thiết diện qua đỉnh tạo với đáy một góc 600. Tính diện tích của thiết diện này.

Hướng dẫn giải

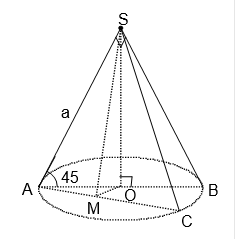
a) Thiết diện qua trục là tam giác SAB vuông cân tại S nên: \(\widehat A = \widehat B = {45^0}.\)

Diện tích xung quanh hình nón là: \({S_{xq}} = \pi Rl = \pi .OA.SA = \pi .\frac{a}{{\sqrt 2 }}.a = \frac{{\pi {a^2}}}{{\sqrt 2 }}.\)

Diện tích toàn phần hình nón là: \({S_{tp}} = {S_{xq}} + {S_{day}} = \frac{{\pi {a^2}}}{{\sqrt 2 }} + \frac{{\pi {a^2}}}{2} = \left( {\frac{1}{{\sqrt 2 }} + \frac{1}{2}} \right)\pi {a^2}.\)

b) Thể tích khối nón là: \(V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi .O{A^2}.SO = \frac{1}{3}\pi .\frac{{{a^2}}}{2}.\frac{a}{{\sqrt 2 }} = \frac{{\pi {a^3}}}{{6\sqrt 2 }}.\)

c) Thiết diện (SAC) qua đỉnh tạo với đáy một góc 600.

Kẻ \(OM \bot AC \Rightarrow SM \bot AC \Rightarrow \widehat {SMO} = {60^0}.\)

Do tam giác SMO vuông tại O nên \(OM = \frac{{SO}}{{\tan 60}} = \frac{{a\sqrt 6 }}{6}.\)

Tam giác OAM vuông tại M nên: \(AM = \sqrt {O{A^2} - O{M^2}} = \frac{{a\sqrt 3 }}{3}\).

Tam giác ABC vuông tại C (nội tiếp đường tròn) suy ra \(BC \bot AC.\)

Suy ra OM là đường trung bình của tam giác ABC.

Nên \(AC = 2AM = \frac{{2a\sqrt 3 }}{3}.\)   

Ta có: \(SM = SO.\sin {60^0} = \frac{{a\sqrt 6 }}{3}.\)

Vậy diện tích thiết diện là: \({S_{SAC}} = \frac{1}{2}.SM.AC = \frac{1}{2}.\frac{{a\sqrt 6 }}{3}.\frac{{2a\sqrt 3 }}{3} = \frac{{{a^2}\sqrt 2 }}{3}.\)

Câu 1: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh đều bằng a. Tính diện tích xung quanh S của hình trụ tròn xoay ngoại tiếp lăng trụ.

Hướng dẫn giải

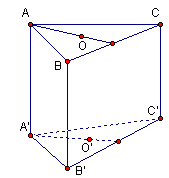
Diện tích xung quanh mặt trụ được tính theo công thức \({S_{xq}} = 2\pi .R.l\).

Gọi R là bán kính đường tròn ngoại tiếp \(\Delta ABC\).

\(\Rightarrow R = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\); \(l =AA'=a\).

Vậy diện tích cần tìm là \({S_{xq}} = 2\pi .\frac{{a\sqrt 3 }}{3}.a = 2\pi \frac{{{a^2}\sqrt 3 }}{3}\) (đvdt).

Câu 2: Một hình trụ có bán kính đáy R=5 cm và khoảng cách giữa hai đáy bằng 7 cm.

a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.

b) Tính thể tích của khối trụ

c) Cắt khối trụ bởi một mặt phẳng song song với trục và cách trụ 3cm. Hãy tính diện tích của thiết diện được tạo nên.

Hướng dẫn giải

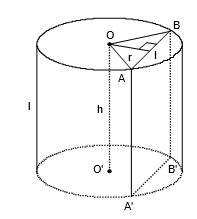
Hình trụ có bán kính đáy R=5 và chiều cao h=7.

a) Diện tích xung quanh hình trụ là: \({S_{xq}} = 2\pi Rl = 2\pi .5.7 = 70\pi \,\,(c{m^2})\)

Diện tích toàn phần hình trụ là: \({S_{tp}} = {S_{xq}} + 2.{S_{day}} = 70\pi + 2\pi {.5^2} = 120\pi \,\,(c{m^2}).\)

b) Thể tích khối trụ là: \(V = \pi {R^2}h = \pi {.5^2}.7 = 175\pi \,\,(c{m^3}).\)

c) Gọi I là trung điểm của AB suy ra OI=3cm.

\(IB = \sqrt {O{B^2} - O{I^2}} = \sqrt {{5^2} - {3^2}} = 4.\)

Ta có: AB=2IB=8.

Dễ thấy thiết diện ABB'A' là hình chữ nhật.

Vậy diện tích thiết diện là: \({S_{ABB'A'}} = AB.AA' = 8.7 = 56\,\,(c{m^2}).\)

Câu 1: Trong không gian cho hai điểm A, B cố định và có độ dài \(AB = 20cm\). Gọi d là một đường thẳng thay đổi luôn đi qua A và cách B một khoảng bằng \(10cm\). Chứng tỏ rằng đường thẳng d luôn nằm trên một mặt nón, hãy xác định trục và góc ở đỉnh của mặt nón đó.

Câu 2: Cho hình chóp tứ giác đều S.ABCD có chiều cao  SO = h và góc \(\widehat {SAB} = \alpha (\alpha  > {45^0})\) . Tính diện tích xung quanh của hình nón đỉnh S và có đường tròn đáy ngoại tiếp hình vuông ABCD của hình chóp.

Câu 3: Chứng minh rằng trong một khối nón tròn xoay, góc ở đỉnh là góc lớn nhất trong số các góc được tạo nên bởi hai đường sinh của khối nón đó.

Câu 4: Một hình trụ có bán kính r và chiều cao \(h = r \sqrt{3}\).

a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.

b) Tính thể tích khối trụ tạo nên bởi hình trụ đã cho.

c) Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng \(30^o\).Tính khoảng cách giữa đường thẳng AB và trục của hình trụ.

Câu 5: Cho mặt trụ xoay và một điểm S cố định nằm ngoài . Một đường thẳng d thay đổi luôn luôn đi qua S cắt tại A và B. Chứng minh rằng trung điểm I của đoạn thẳng AB luôn luôn nằm trên một mặt trụ xác định.

Câu 1: Khẳng định nào sau đây là sai? 

A. Thể tích khối cầu có bán kính R: \(V = \frac{4}{3}\pi {R^3}\).

B.  Diện tích mặt cầu có bán kính R: \(S = 4\pi {R^2}\).

C. Thể tích của khối trụ có bán kính đáy R và chiều cao h là:  \(V = \pi {R^2}h\).

D. Thể tích của khối nón có bán kính đáy R và chiều cao h là:  \(V = \frac{1}{3}{\pi ^2}{R^2}h\).

Câu 2: Một tam giác ABC vuông tại A có AB = 6, AC = 8. Cho đường gấp khúc ABC quay quanh cạnh AC được hình nón có diện tích xung quanh và diện tích toàn phần lần lượt là S1, S2. Hãy chọn kết quả đúng.

A.  \(\frac{{{S_1}}}{{{S_2}}} = \frac{8}{5}\)

B.  \(\frac{{{S_1}}}{{{S_2}}} = \frac{5}{8}\)

C.  \(\frac{{{S_1}}}{{{S_2}}} = \frac{5}{9}\)

D.  \(\frac{{{S_1}}}{{{S_2}}} = \frac{9}{5}\)

Câu 3: Cho hình hộp chữ nhật ABCD.A′B′C′D′ có \(AB=AD=2a, AA' = 3\sqrt 2 a.\) Tính điện tích toàn phần S của hình trụ có hai đáy lần lượt ngoại tiếp hai đáy của hình hộp chữ nhật đã cho.

A.  \(S=16 \pi a^2\)

B.  \(S=20 \pi a^2\)

C.  \(S=7 \pi a^2\)

D. \(S=12 \pi a^2\)

Câu 4: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông cạnh a và cạnh bên bằng 2a. Tính diện tích xung quanh \(S_{xq}\) của hình nón có đỉnh là tâm O của hình vuông A’B’C’D’ và đáy là hình tròn nội tiếp hình vuông ABCD.​

A.  \(S_{xq}=\frac{{\pi {a^2}\sqrt {17} }}{4}\)

B.  \({S_{xq}} = \pi {a^2}\) 

C.  \({S_{xq}} = \frac{{\pi {a^2}\sqrt {17} }}{2}\)

D.  \({S_{xq}} = \pi {a^2}\sqrt {17}\)

Câu 5: Trong một chiếc hộp hình trụ người ta bỏ vào đó 6 quả banh tennis, biết rằng đáy của hình trụ bằng hình tròn lớn trên quả banh và chiều cao hình trụ bằng 6 lần đường kính của quả banh. Gọi V1 là tổng thể tích của 6 quả banh và V2 là thể tích của khối trụ. Tính tỉ số  \(\frac{V_1}{V_2}\)?

A.  \(\frac{{{V_1}}}{{{V_2}}} = \frac{1}{3}\)

B.   \(\frac{{{V_1}}}{{{V_2}}} = \frac{2}{3}\) 

C.  \(\frac{{{V_1}}}{{{V_2}}} = \frac{1}{2}\)

D.  \(\frac{{{V_1}}}{{{V_2}}} = \frac{1}{4}\)

Qua bài học giúp học sinh nắm được một số nội dung chính như sau:

• Nắm được sự tạo thành mặt tròn xoay ,các yếu tố của mặt tròn xoay.
• Hiểu được mặt nón tròn xoay ,góc ở đỉnh ,trục,đường sinh của mặt nón
• Phân biệt các khái niệm: Mặt nón,hình nón khối nón tròn xoay,nắm vững công thức tính toán diện tích xung quanh. Biết tính diện tích xung quanh và thể tích .