Toán 12 Chương 1 Bài 3: Khái niệm về thể tích của khối đa diện
Bài học Khái niệm về thể tích của khối đa diện bao gồm kiến thức thức cần nhớ và các dạng Toán liên quan được eLib tóm tắt một cách chi tiết, dễ hiểu. Sau đây mời các em cùng tham khảo.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Tính chất của thể tích khối đa diện
- Hai khối đa diện bằng nhau thì có thể tích bằng nhau.
- Nếu 1 khối đa diện được phân chia thành các khối đa diện nhỏ thì thể tích của nó bằng tổng thể tích của các khối đa diện nhỏ.
- Khối lập phương có cạnh bằng 1 thì có thể tích bằng 1.
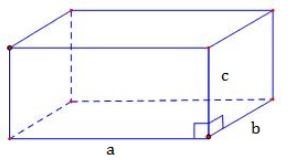
1.2. Thể tích khối hộp chữ nhật
Giả sử có 1 khối hộp chữ nhật với 3 kích thước a, b, c đều là những số dương. Khi đó thể tích của nó là: \(V=a.b.c\).
1.3. Thể tích khối chóp
- Thể tích của 1 khối chóp bắng một phần ba tích số của mặt đáy và chiều cao khối chóp đó: \(V=\frac{1}{3}S_{day}.h.\)
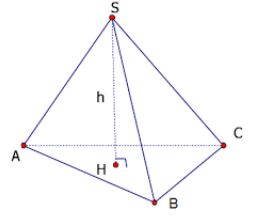
\(V_{S.ABCD}=\frac{1}{3}S_{ABC}.SH\)
- Công thức tỉ số thể tích của khối chóp tam giác:
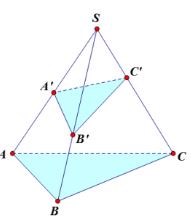
Trên các đường thẳng SA, SB, SC của hình chóp S.ABC ta lấy lần lượt các điểm A', B', C'. Ta có:
\({V_{S.A'B'C'}} = \dfrac{{SA'.SB'.SC'}}{{SA.SB.SC}}{V_{S.ABC}}\).
1.4. Thể tích khối lăng trụ
Thể tích của khối lăng trụ bằng tích số của diện tích mặt đáy với chiều cao của khối lăng trụ đó: \(V=S_{day}.h.\)
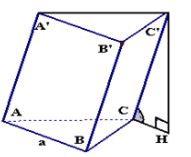
\(V_{ABC.A'B'C'}=S_{ABC}.C'H\)
2. Bài tập minh họa
2.1. Dạng 1. Tính thể tích khối chóp
Câu 1: Cho hình chóp S.ABC có tam giác ABC vuông tại B, \(AB=a \sqrt 2, AC=a \sqrt 3\), cạnh bên SA vuông góc với mặt phẳng đáy và \(SB=a \sqrt 3.\) Tính thể tích khối chóp S.ABC.
Hướng dẫn giải
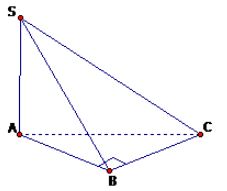
Tam giác ABC vuông tại B nên \(BC = \sqrt {A{C^2} - A{B^2}} = a.\)
Suy ra: \({{\rm{S}}_{\Delta {\rm{ABC}}}} = \frac{1}{2}BA.BC = \frac{1}{2}.a\sqrt 2 .a = \frac{{{a^2}.\sqrt 2 }}{2}\)
Tam giác SAB vuông tại A có \(SA = \sqrt {S{B^2} - A{B^2}} = a.\)
Vậy thể tích khối chóp S.ABC là: \({V_{S.ABC}} = \frac{1}{3}.{S_{ABC}}.SA = \frac{1}{3}.\frac{{{a^2}.\sqrt 2 }}{2}.a = \frac{{{a^3}.\sqrt 2 }}{6}.\)
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \(a\sqrt2\), cạnh bên SA vuông góc với mặt phẳng đáy và \(SC=a \sqrt5\). Tính thể tích khối chóp S.ABCD.
Hướng dẫn giải
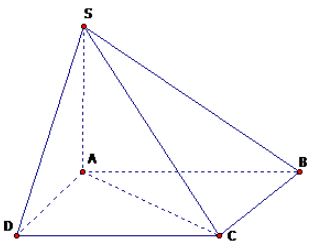
Diện tích ABCD: \({{\rm{S}}_{{\rm{ABCD}}}} = {\left( {a\sqrt 2 } \right)^2} = 2{a^2}.\)
Ta có: \(AC = AB.\sqrt 2 = a\sqrt 2 .\sqrt 2 = 2a.\)
Tam giác SAC vuông tại A nên: \(SA = \sqrt {S{C^2} - A{C^2}} = a\).
Vậy thể tích khối chóp S.ABCD là: \({V_{S.ABCD}} = \frac{1}{3}.{S_{ABCD}}.SA = \frac{1}{3}.2{a^2}.a = \frac{{2{a^3}}}{3}.\)
2.2. Dạng 2. Thể tích khối lăng trụ
Câu 1: Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, AB=a, \(AC=a\sqrt3\), cạnh A'B = 2a. Tính thể tích khối lăng trụ ABC.A'B'C'.
Hướng dẫn giải
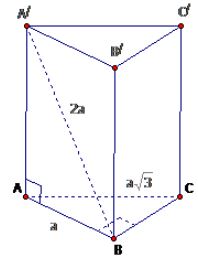
Tam giác ABC vuông tại B nên \(BC=\sqrt {A{C^2} - A{B^2}} = a\sqrt 2.\)
Suy ra: \({S_{ABC}} = \frac{1}{2}AB.BC = \frac{{{a^2}\sqrt 2 }}{2}.\)
Tam giác A'AB vuông tại A nên: \(A'A = \sqrt {A'{B^2} - A{B^2}} = a\sqrt 3 .\)
Vậy thể tích khối lăng trụ là: \({V_{ABC.A'B'C'}} = {S_{ABC}}.A'A = \frac{{{a^3}\sqrt 6 }}{2}.\)
Câu 2: Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh \(2a\sqrt3\), hình chiếu vuông góc của A' lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC, cạnh A'A hợp với mặt đáy (ABC) một góc 300. Tính thể tích khối lăng trụ ABC.A'B'C'.
Hường dẫn giải
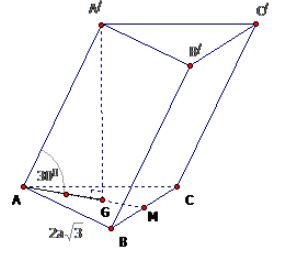
Gọi M là trung điểm của BC.
G là trọng tâm tam giác ABC suy ra: \(A'G \bot (ABC)\).
Do đó AG là hình chiếu vuông góc của AA' lên mặt phẳng (ABC).
Suy ra: \(\left( {\widehat {{A^/}A,(ABC)}} \right) = \widehat {{A^/}AG} = {30^0}.\)
Tam giác ABC đều cạnh \(2a\sqrt3\) nên: \({S_{ABC}} = {\left( {2a\sqrt 3 } \right)^2}.\frac{{\sqrt 3 }}{4} = 3{a^2}\sqrt 3.\)
Tam giác A'AG vuông tại G có \(\widehat A = {30^0},AG = \frac{2}{3}AM = \frac{2}{3}.2a\sqrt 3 .\frac{{\sqrt 3 }}{2} = 2a.\)
Suy ra: \(A'G = AG.\tan {30^0} = \frac{{2a\sqrt 3 }}{3}.\)
Vậy: \({V_{ABC.{A'}{B'}{C'}}} = {S_{ABC}}.{A'}A = 6{a^3}.\)
2.3. Dạng 3. Công thức tính tỷ số thể tích
Câu 1: Cho hình chóp S.ABC có tam giác ABC đều cạnh 2a, cạnh bên SA vuông góc với mặt phẳng đáy và \(SA=a\sqrt3.\)Gọi M, N lần lượt là trung điểm của SB và SC. Tính thể tích khối chóp S.AMN và A.BCNM.
Hướng dẫn giải
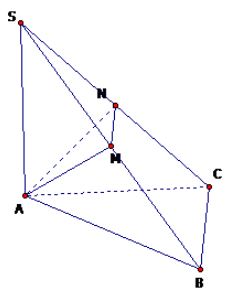
Khối chóp S.AMN và S.ABC có chung đỉnh S và góc ở đỉnh S.
Do đó theo công thức tỷ số thể tích, ta có:
\(\frac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \frac{{{\rm{SA}}}}{{{\rm{SA}}}}.\frac{{SM}}{{SB}}.\frac{{SN}}{{SC}} = 1.\frac{1}{2}.\frac{1}{2} = \frac{1}{4}\)
Suy ra: \({V_{S.AMN}} = \frac{{{V_{S.ABC}}}}{4} = \frac{{\frac{1}{3}.{a^2}\sqrt 3 .a\sqrt 3 }}{4} = \frac{{{a^3}}}{4}\)
Và: \({V_{A.BCNM}} = \frac{3}{4}.{V_{S.ABC}} = {\frac{{3a}}{4}^3}.\)
Câu 2: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, M và N theo thứ tự là trung điểm của SA và SB. Tính tỉ số thể tích \(\frac{{{V_{S.CDMN}}}}{{{V_{S.CDAB}}}}\).
Hướng dẫn giải
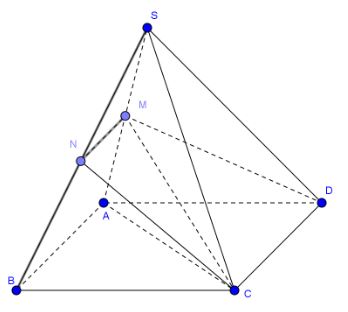
Ta có:
\({V_{S.MNCD}} = {V_{S.MCD}} + {V_{S.MNC}}\) và \({V_{S.ABCD}} = {V_{S.ACD}} + {V_{S.ABC}}\).
Khi đó: \(\frac{{{V_{S.MCD}}}}{{{V_{S.ACD}}}} = \frac{{SM}}{{SA}} = \frac{1}{2} \Leftrightarrow {V_{S.MCD}} = \frac{1}{4}{V_{S.ABCD}}\)
Mặt khác: \(\frac{{{V_{S.MNC}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SA}}.\frac{{SN}}{{SB}} = \frac{1}{4} \Rightarrow {V_{S.MNC}} = \frac{1}{8}{V_{S.ABCD}}\)
Từ trên suy ra \({V_{S.MNCD}} = \left( {\frac{1}{4} + \frac{1}{8}} \right){V_{S.ABCD}} = \frac{3}{8}{V_{S.ABCD}}\).
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân ở B, AC=a√2, SA vuông góc với mặt phẳng (ABC), SA = a. Tính thể tích khối chóp S.ABC
Câu 2: Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có AB = 2a, AD = a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, góc giữa SC và mặt phẳng S.ABCD bằng 60º. Tính theo a thể tích khối chóp S.ABCD
Câu 3: Cho hình chóp S.ABC có cạnh bên SA vuông góc với đáy và AB = a, AC = 2a, góc BAC = 120º. Mặt phẳng (SBC) tạo với đáy một góc 60º. Tính theo a thể tích khối chóp S.ABC
Câu 4: Cho khối chóp S.ABCD có ABCD là hình chữ nhật, AD = 2a, AB = a. Gọi H là trung điểm AD, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết SA=a√5
Câu 5: Cho khối chóp S.ABC có tam giác ABC vuông tại B, AB = 3a, AC = 6a. Hình chiếu của S trên mặt phẳng (ABC) là điểm H thuộc đoạn AB sao cho AH = 2HB. Biết SC hợp với (ABC) một góc bằng 60º . Tính thể tích khối chóp S.ABC.
3.2 Bài tập trắc nghiệm
Câu 1. Cho khối tứ diện đều ABCD có cạnh bằng a. Gọi B’, C’ lần lượt là trung điểm của các cạnh AB và AC. Tính thể tích V của khối tứ diện AB’C’D theo a.
A. \(V = \frac{{{a^3}\sqrt 3 }}{{48}}\)
B. \(V = \frac{{{a^3}\sqrt 2 }}{{48}}\)
C. \(V = \frac{{{a^3}}}{{24}}\)
D. \(V = \frac{{{a^3}\sqrt 2 }}{{24}}\)
Câu 2. Cho hình lăng trụ ABC.A’B’C’ vì M là trung điểm của CC’. Gọi khối đa diện (H) là phần còn lại của khối lăng trụ ABC.A’B’C’ sau khi cắt bỏ đi khối chóp M.ABC. Tính tỷ số thể tích của (H) và khối chóp M.ABC.
A. \(\frac{{{V_{(H)}}}}{{{V_{M.ABC}}}} = \frac{1}{6}\)
B. \(\frac{{{V_{(H)}}}}{{{V_{M.ABC}}}} = 6\)
C. \(\frac{{{V_{(H)}}}}{{{V_{M.ABC}}}} = \frac{1}{5}\)
D. \(\frac{{{V_{(H)}}}}{{{V_{M.ABC}}}} = 5\)
Câu 3. Biết thể tích của khối lăng trụ ABC.A'B'C' bằng V. Tính thể tích \(V_1\) tứ diện A'ABC' theo V.
A. \(V_1=\frac{V}{4}\)
B. \(V_1=2V\)
C. \(V_1=\frac{V}{2}\)
D. \(V_1=\frac{V}{3}\)
Câu 4. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a và đường thẳng A’C tạo với mặt phẳng (ABB’A’) một góc 300. Tính thể tích V của khối lăng trụ ABC.A’B’C’.
A. \(V = \frac{{{a^3}\sqrt 6 }}{{12}}\)
B. \(V = \frac{{{a^3}\sqrt 6 }}{8}\)
C. \(V = \frac{{{a^3}\sqrt 6 }}{{4}}\)
D. \(V = \frac{{{a^3}\sqrt 6 }}{{2}}\)
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm E sao cho SE=2EC. Tính thể tích V của khối tứ diện SEBD.
A. \(V=\frac{1}{6}\)
B. \(V=\frac{1}{12}\)
C. \(V=\frac{1}{3}\)
D. \(V=\frac{2}{3}\)
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Khái niệm về thể tích của khối đa diện Toán 12 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Biết cách tính thể tích các khối chóp đặc biệt.
- Làm được các bài tập liên quan.
