Toán 12 Chương 1 Bài 1: Khái niệm về khối đa diện

a) Khối lăng trụ

- Hình lăng trụ:

• 2 đáy là 2 đa giác bằng nhau.
• Các cạch bên song song và bằng nhau.
• Các mặt bên là các hình bình hành.

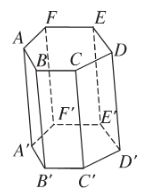
- Khối lăng trụ là phần không gian giới hạn bởi hình lăng trụ. \(\sqrt 2\)

- Hình lăng trụ đứng:

• Định nghĩa: Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với mặt đáy.

• Tính chất: Các mặt bên của hình lăng trụ đứng là các hình chữ nhật và vuông góc với mặt đáy.

- Hình lăng trụ đều:

• Định nghĩa: Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.

• Tính chất: Các mặt bên của hình lăng trụ đều là các hình chữ nhật bằng nhau. 

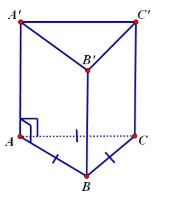
b) Khối chóp

- Hình chóp:

• Đáy là đa giác.
• Các mặt bên là các tam giác chung đỉnh.

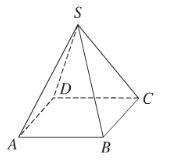
- Khối chóp là phần không gian được giới hạn được bởi hình chóp.

• Đáy khối chóp là tam giác: khối chóp tam giác.
• Đáy khối chóp là tứ giác: khối chóp tứ giác giác.
• Đáy khối chóp là ngũ giác: khối chóp ngũ giác.

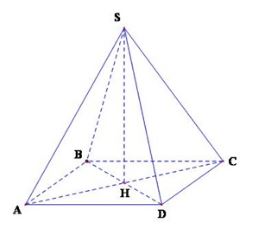
- Hình chóp đều:

+ Định nghĩa: Hình chóp đều là hình chóp có các cạnh bên bằng nhau và mặt đáy là một đa giác đều.

+ Tính chất: Chân đường cao của hình chóp đều trùng với tâm của đa giác đáy.

+ Phương pháp chứng minh hình chóp đều:

• Hình chóp là hình chóp đều khi và chỉ khi đáy của nó là đa giác đều và chân đường cao của nó trùng với tâm của đa giác đáy.

• Hình chóp là hình chóp đều khi và chỉ khi đáy của nó là đa giác đều và các cạnh bên tạo với mặt đáy các góc bằng nhau.

Khối đa diện được giới hạn bởi hữu hạn đa giác thỏa mãn điều kiện:

• Hai đa giác bất kì không có điểm chung, hoặc có một điểm chung hoặc có chung một cạnh.
• Mỗi cạnh đa giác là cạnh chung của đúng hai cạnh đa giác.

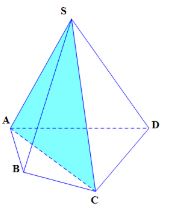
- Cho khối chóp tứ giác S.ABCD. Ta xét 2 khối chóp tam giác S.ABC và S.ACD. Ta thấy:

• Hai khối chóp đó không có điểm trong chung, nghĩa là điểm trong của khối chóp này không phải điểm trong của khối chóp kia.
• Hợp của 2 khối chóp S.ABCS.ABC và S.ACDS.ACD chính là khối chóp S.ABCDS.ABCD.

- Trong trường hợp đó ta nói rằng: Khối đa diện S.ABCD được phân chia thành 2 khối đa diện S.ABC và S.ACD.

- Ta cũng nói: Hai khối đa diện S.ABC và S.ACD được ghép lại thành khối đa diện S.ABCD.

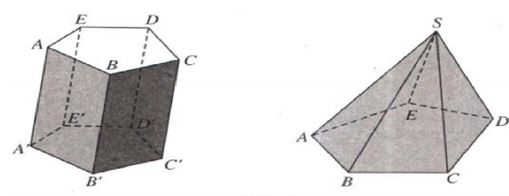
Câu 1: Kể tên các mặt của hình lăng trụ ABCDE.A’B’C’D’E’ và hình chóp S.ABCDE

Hướng dẫn giải

- Các mặt của hình lăng trụ ABCDE.A’B’C’D’E’là: ABB’A’, BCC’B’, CDD’C’, DEE’D’, EAA’E’, ABCDE, A’B’C’D’E’

- Các mặt của hình chóp S.ABCDE là: SAB, SBC, SCD, SDE, SAE, ABCDE

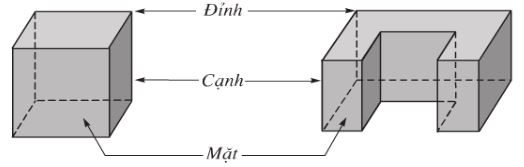
Câu 2: Giải thích tại sao hình dưới đây không phải là một khối đa diện?

Hướng dẫn giải

Hình đa diện có tính chất: Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.

Nhưng hình trên có cạnh AB là cạnh chung có 4 đa giác (không thỏa mãn t/c).

Câu 1: Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng hai lăng trụ ABD.A’B’D’ và BCD.B’C’D’ bằng nhau.

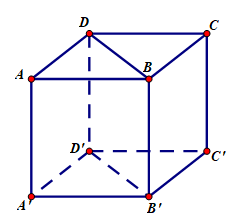
Câu 2: Hãy chia một khối lập phương thành năm khối tứ diện.

Câu 1. Cho hình chóp S.ABC có SA=a, \(SB = a\sqrt 2 ;SC = a\sqrt 3 \). Tính thể tích lớn nhất V.max của khối chóp đã cho.

A. \({V_{\max }} = {a^3}\sqrt 6 .\)

B. \({V_{\max }} = \frac{{{a^3}\sqrt 6 }}{2}.\)

C. \({V_{\max }} = \frac{{{a^3}\sqrt 6 }}{3}.\)

D. \({V_{\max }} = \frac{{{a^3}\sqrt 6 }}{6}.\)

Câu 2. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có độ dài đường chéo \(AC' = \sqrt {18} .\) Gọi S là diện tích toàn phần của hình hộp đã cho. Tìm giá trị lớn nhất S.max của S.

A. \(36\sqrt 3 \)

B. \(18\sqrt 3 \)

C. 18

D. 36

Câu 3. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Tồn tại một hình đa diện có số mặt lớn hơn số cạnh

B. Tồn tại một hình đa diện có số mặt lớn hơn số đỉnh

C. Trong một hình đa diện số mặt luôn lớn hơn hoặc bằng số đỉnh

D. Tồn tại một hình đa diện có số đỉnh lớn hơn số cạnh

Câu 4. Khẳng định nào sau đây là khẳng định sai?

A. Mỗi cạnh của khối đa diện là cạnh chung của đúng 2 mặt của khối đa diện.

B. Hai mặt bất kì của khối đa diện luôn có ít nhất một điểm chung.

C. Mỗi đỉnh của khối đa diện là đỉnh chung của ít nhất 3 mặt.

D. Mỗi mặt của khối đa diện có ít nhất ba cạnh.

Câu 5. Hình nào sau đây không phải là hình đa diện?

Qua bài học này, các em cần nắm được những nội dung sau:

• Khái niệm về khối đa diện
• Phân loại được các khối đa diện.