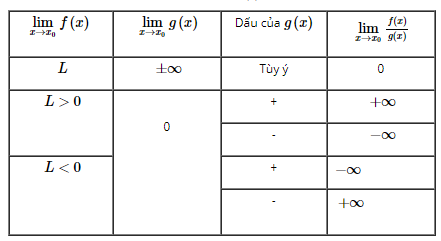
Giải bài tập SGK Toán 11 Chương 4 Bài 2: Giới hạn của hàm số

Dùng định nghĩa tìm các giới hạn sau:

a) $\underset{x\rightarrow 4}{lim} \ \frac{x+1}{3x - 2}$

b) $\underset{x \rightarrow +\infty }{lim}\frac{2-5x^{2}}{x^{2}+3}$

Phương pháp giải

Sử dụng kết quả của định nghĩa 1 trang 124 và định nghĩa 3 SGK trang 128

Hướng dẫn giải

a) Hàm số $f(x) = \dfrac{x +1}{3x - 2}$ xác định trên $D=\mathbb R\backslash \left\{ {{2 \over 3}} \right\}$ và ta có $x = 4 \in D$

Giả sử $(x_n)$ là dãy số bất kì và $x_n ∈ D$; $x_n≠ 4$ và $x_n→ 4$ khi $n \to  + \infty$ hay $\lim {x_n} = 4$

Ta có $\lim f(x_n) = \lim \dfrac{x_{n} +1}{3x_{n} - 2}$ $= \dfrac{{\lim {x_n} + 1}}{{3\lim {x_n} - 2}}$ $= \dfrac{4 + 1}{3. 4 - 2} = \dfrac{1}{2}$

Vậy $\underset{x\rightarrow 4}{\lim}$ $\dfrac{x +1}{3x - 2}$ = $\dfrac{1}{2}$.

b) Hàm số $f(x)$ = $\dfrac{2-5x^{2}}{x^{2}+3}$ xác định trên $\mathbb R$.

Giả sử $(x_n)$ là dãy số bất kì và $x_n→ +∞$ khi $n \to  + \infty$ hay $\lim {x_n} =  + \infty$

$\Rightarrow \lim \dfrac{1}{{x_n^2}} = 0$

Ta có $\lim f(x_n) = \lim \dfrac{2-5x^{2}_{n}}{x^{2}_{n}+3}$ $= \lim \dfrac{{x_n^2\left( {\dfrac{2}{{x_n^2}} - 5} \right)}}{{x_n^2\left( {1 + \dfrac{3}{{x_n^2}}} \right)}}$ $= \lim \dfrac{\dfrac{2}{x^{2}_{n}}-5}{1+\dfrac{3}{x^{2}_{n}}}$ $= \dfrac{{\lim \dfrac{2}{{x_n^2}} - 5}}{{1 + \lim \dfrac{3}{{x_n^2}}}} = \dfrac{{0 - 5}}{{1 + 0}}$ $= -5$

Vậy $\underset{x\rightarrow +\infty }{\lim}$ $\dfrac{2-5x^{2}}{x^{2}+3} = -5$.

Cho hàm số $f(x) =\left\{\begin{matrix} \sqrt{x}+1&nếu &x\geq 0 \\ 2x&nếu& x <0 \end{matrix}\right.$

và các dãy số $(u_n)$ với  $u_n =\frac{1}{n}$, $(v_n)$ với $v_n = -\frac{1}{n}$

Tính $lim u_n, lim v_n, lim f (u_n)$và $lim (v_n).$

Từ đó có kết luận gì về giới hạn của hàm số đã cho khi x → 0?

Phương pháp giải

- Sử dụng giới hạn cơ bản $\lim \dfrac{1}{{{n^k}}} = 0$ với $k\in N^*$

- Thay $u_n,v_n$ vào $f(x)$ và tính giới hạn.

Hướng dẫn giải

$\begin{array}{l} \lim {u_n} = \lim \dfrac{1}{n} = 0\\ \lim {v_n} = \lim \left( { - \dfrac{1}{n}} \right) = 0\\ {u_n} = \dfrac{1}{n} > 0 \Rightarrow f\left( {{u_n}} \right) = \sqrt {\dfrac{1}{n}} + 1\\ \Rightarrow \lim f\left( {{u_n}} \right) = \lim \left( {\sqrt {\dfrac{1}{n}}  + 1} \right) = 1\\ {v_n} = - \dfrac{1}{n} < 0 \Rightarrow f\left( {{v_n}} \right) = - \dfrac{2}{n}\\ \Rightarrow \lim f\left( {{v_n}} \right) = \lim \left( { - \dfrac{2}{n}} \right)= 0 \end{array}$

Do $\lim f\left( {{u_n}} \right) = 1$ nên $\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = 1$.

$\lim f\left( {{v_n}} \right) = 0$ nên $\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = 0$.

Do đó $\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right)$ nên không tồn tại giới hạn của hàm số tại $x = 0$.

Vậy hàm số đã cho không có giới hạn khi $x \to 0$.

Tính các giới hạn sau:

a) $\underset{x\rightarrow -3}{lim} \frac{x^{2 }-1}{x+1}$

b) $\underset{x\rightarrow -2}{lim}\frac{4-x^{2}}{x + 2}$

c) $\underset{x\rightarrow 6}{lim} \frac{\sqrt{x + 3}-3}{x-6}$

d) $\underset{x\rightarrow +\infty }{lim} \frac{2x-6}{4-x}$

e) $\underset{x\rightarrow +\infty }{lim} \frac{17}{x^{2}+1}$

f) $\underset{x\rightarrow +\infty }{lim} \frac{-2x^{2}+x -1}{3 +x}$

Phương pháp giải

Nếu hàm số $y=f(x)$ xác định tại $x=x_0$ thì $\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)$.

Nếu giới hạn hàm số có dạng vô định, tìm cách khử dạng vô định.

Hướng dẫn giải

a) $\underset{x\rightarrow -3}{\lim}$ $\dfrac{x^{2 }-1}{x+1}$ $= \dfrac{{\mathop {\lim }\limits_{x \to  - 3} \left( {{x^2} - 1} \right)}}{{\mathop {\lim }\limits_{x \to  - 3} \left( {x + 1} \right)}}$ $= \dfrac{{\mathop {\lim }\limits_{x \to  - 3} {x^2} - \mathop {\lim }\limits_{x \to  - 3} 1}}{{\mathop {\lim }\limits_{x \to  - 3} x + \mathop {\lim }\limits_{x \to  - 3} 1}}$ = $\dfrac{(-3)^{2}-1}{-3 +1} = -4$.

b) $\underset{x\rightarrow -2}{\lim}$ $\dfrac{4-x^{2}}{x + 2}$ = $\underset{x\rightarrow -2}{\lim}$ $\dfrac{ (2-x)(2+x)}{x + 2}$ = $\underset{x\rightarrow -2}{\lim} (2-x) =2-(-2)= 4$

c) $\underset{x\rightarrow 6}{\lim}$ $\dfrac{\sqrt{x + 3}-3}{x-6}$ = $\underset{x\rightarrow 6}{\lim}\dfrac{(\sqrt{x + 3}-3)(\sqrt{x + 3}+3 )}{(x-6) (\sqrt{x + 3}+3 )}$ 
= $\underset{x\rightarrow 6}{\lim}$ $\dfrac{x +3-9}{(x-6) (\sqrt{x + 3}+3 )}$ $= \mathop {\lim }\limits_{x \to 6} \dfrac{{x - 6}}{{\left( {x - 6} \right)\left( {\sqrt {x + 3}  + 3} \right)}}$ $= \mathop {\lim }\limits_{x \to 6} \dfrac{1}{{\sqrt {x + 3}  + 3}}$ $= \dfrac{1}{{\mathop {\lim }\limits_{x \to 6} \left( {\sqrt {x + 3}  + 3} \right)}}$ $= \dfrac{1}{{\mathop {\lim }\limits_{x \to 6} \left( {\sqrt {x + 3} } \right) + 3}}$ $= \dfrac{1}{{\sqrt {6 + 3}  + 3}}$= $\dfrac{1}{6}$.

d) $\underset{x\rightarrow +\infty }{\lim}$ $\dfrac{2x-6}{4-x}$ $= \mathop {\lim }\limits_{x \to  + \infty } \dfrac{{x\left( {2 - \dfrac{6}{x}} \right)}}{{x\left( {\dfrac{4}{x} - 1} \right)}}$ $= \mathop {\lim }\limits_{x \to  + \infty } \dfrac{{2 - \dfrac{6}{x}}}{{\dfrac{4}{x} - 1}}$ $= \dfrac{{2 - \mathop {\lim }\limits_{x \to  + \infty } \dfrac{6}{x}}}{{\mathop {\lim }\limits_{x \to  + \infty } \dfrac{4}{x} - 1}}$ $= \dfrac{{2 - 0}}{{0 - 1}}$ $= -2$

e) $\underset{x\rightarrow +\infty }{\lim}$ $\dfrac{17}{x^{2}+1} = 0$ vì:

$\underset{x\rightarrow +\infty }{\lim}$  $(x^2+ 1) =$ $\underset{x\rightarrow +\infty }{\lim} x^2( 1 + \dfrac{1}{x^{2}}) = +∞$

f) $\underset{x\rightarrow +\infty }{\lim}$ $\dfrac{-2x^{2}+x -1}{3 +x}$ $= \mathop {\lim }\limits_{x \to  + \infty } \dfrac{{{x^2}\left( { - 2 + \dfrac{1}{x} - \dfrac{1}{{{x^2}}}} \right)}}{{{x^2}\left( {\dfrac{3}{{{x^2}}} + \dfrac{1}{x}} \right)}}$ $=\underset{x\rightarrow +\infty }{\lim}\dfrac{-2+\dfrac{1}{x} -\dfrac{1}{x^{2}}}{\dfrac{3}{x^{2}} +\dfrac{1}{x}}$

Vì $\mathop {\lim }\limits_{x \to  + \infty } \left( {\dfrac{3}{{{x^2}}} + \dfrac{1}{x}} \right) = 0$; ${\dfrac{3}{{{x^2}}} + \dfrac{1}{x}}>0$ khi $x \to  + \infty$

và $\mathop {\lim }\limits_{x \to  + \infty } \left( { - 2 + \dfrac{1}{x} - \dfrac{1}{{{x^2}}}} \right)$ $=  - 2 + \mathop {\lim }\limits_{x \to  + \infty } \dfrac{1}{x} - \mathop {\lim }\limits_{x \to  + \infty } \dfrac{1}{{{x^2}}}$ $=  - 2 + 0 - 0 =  - 2 < 0$

Vậy $\underset{x\rightarrow +\infty }{\lim}$ $\dfrac{-2x^{2}+x -1}{3 +x}$$=\underset{x\rightarrow +\infty }{\lim}\dfrac{-2+\dfrac{1}{x} -\dfrac{1}{x^{2}}}{\dfrac{3}{x^{2}} +\dfrac{1}{x}}$ $=-\infty$

Tính các giới hạn sau:

a) $\underset{x\rightarrow 2}{lim}\frac{3x -5}{(x-2)^{2}}$

b) $\underset{x\rightarrow 1^{-}}{lim}\frac{2x -7}{x-1}$

c) $\underset{x\rightarrow 1^{+}}{lim}\frac{2x -7}{x-1}$

Phương pháp giải

Sử dụng quy tắc tìm giới hạn của thương $\frac{{f\left( x \right)}}{{g\left( x \right)}}$

Hướng dẫn giải

a) Ta có $\underset{x\rightarrow 2}{\lim} (x - 2)^2= 0$ và $(x - 2)^2> 0$ với $∀x ≠ 2$ và $\underset{x\rightarrow 2}{\lim} (3x - 5) = 3.2 - 5 = 1 > 0$.

Do đó $\underset{x\rightarrow 2}{\lim}$ $\dfrac{3x -5}{(x-2)^{2}} = +∞$.

b) Ta có $\underset{x\rightarrow 1^{-}}{\lim} (x - 1)=0$ và $x - 1 < 0$ với $∀x < 1$ và $\underset{x\rightarrow 1^{-}}{\lim} (2x - 7) = 2.1 - 7 = -5 <0$.

Do đó $\underset{x\rightarrow 1^{-}}{\lim}\dfrac{2x -7}{x-1} = +∞$.

c) Ta có $\underset{x\rightarrow 1^{+}}{\lim} (x - 1) = 0$ và $x - 1 > 0$ với $∀x > 1$ và $\underset{x\rightarrow 1^{+}}{\lim} (2x - 7) = 2.1 - 7 = -5 < 0$.

Do đó $\underset{x\rightarrow 1^{+}}{lim}$ $\dfrac{2x -7}{x-1}= -∞$.

Cho hàm số  $f(x) =\frac{x+2}{x^{2}-9}$ có đồ thị như hình dưới đây:

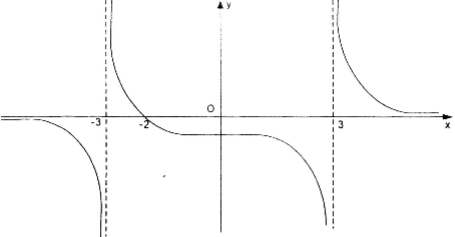
a) Quan sát đồ thị và nêu nhận xét về giá trị hàm số đã cho khi $x \rightarrow -\infty$

$x \rightarrow 3^-$ và $x \rightarrow 3^+$

b) Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:

$\underset{x\rightarrow -\infty }{lim} f(x)$ với f(x) được xét trên khoảng (-3; -3)

$\underset{x\rightarrow 3^{-}}{lim}f(x)$ với f(x) được xét trên khoảng (-3,3)

$\underset{x\rightarrow -3^{+}}{lim}f(x)$ với f(x) được xét trên khoảng (-3; 3)

Phương pháp giải

a) Quan sát đồ thị hàm số.

b) Tính các giới hạn, sử dụng quy tắc tính giới hạn được học và kết luận.

Hướng dẫn giải

a) Nhìn vào đồ thị ta có:

 Khi $x\rightarrow -\infty$ thì $f(x)\rightarrow 0.$

 Khi $x\rightarrow 3$ thì $f(x)\rightarrow -\infty .$

 Khi $x \rightarrow - 3^+$ thì $f(x) \rightarrow +\infty .$

b)  $\lim_{x\rightarrow -\infty }f(x)=\lim_{x\rightarrow -\infty }\frac{x+2}{x^2-9} =\lim_{x\rightarrow -\infty }\frac{\frac{1}{x}+\frac{2}{x^2}}{1-\frac{9}{x^2}}=0$

 $\lim_{x\rightarrow -3^+ }f(x)=\lim_{x\rightarrow -3^+ }\frac{x+2}{x^2-9}=+\infty$

 $\lim_{x\rightarrow 3^- }f(x)=\lim_{x\rightarrow 3^- } \frac{x+2}{x^2-9}=-\infty$

Tính:

a) $\lim_{+\infty } (x^4 - x^2 + x - 1)$

b) $\lim_{-\infty } (-2x^3 + 3x^2 -5 )$

c) $\lim_{-\infty } \sqrt{x^2-2x+5}$

d) $\lim_{+\infty } \frac{\sqrt{x^2+1}+x}{5-2x}$

Phương pháp giải

Sử dụng quy tắc tìm giới hạn của tích $f(x).g(x)$.

Hướng dẫn giải

a)  $\lim_{x\rightarrow +\infty } (x^4 - x^2 + x - 1)$

$=\lim_{x\rightarrow +\infty } x^4(1-\frac{1}{x^2}+\frac{1}{x^3}-\frac{1}{x^4})=+\infty$

b) $\lim_{x\rightarrow -\infty } (-2x^3 + 3x^2 -5 )= \lim_{x\rightarrow -\infty } (-x^3)\left ( 2-\frac{3}{x}+\frac{5}{x^3} \right )=+\infty$

c) $\lim_{x\rightarrow -\infty }\sqrt{x^2-2x+5}= \lim_{x\rightarrow -\infty } \left | x \right |\sqrt{1-\frac{2}{x}+\frac{5}{x^2}}$

$\lim_{x\rightarrow -\infty }\sqrt{x^2-2x+5}=\lim_{x\rightarrow -\infty }(-x) \left ( \sqrt{1-\frac{2}{x}+\frac{5}{x^2}} \right )=+\infty$

d) $\lim_{x\rightarrow +\infty } \frac{\sqrt{x^2+1}+x}{5-2x}= \lim_{x\rightarrow +\infty } \frac{\sqrt{1+\frac{1}{x^2}}+1}{\frac{5}{x}-2}=-1$

Một thấu kính hội tụ có tiêu cự là f. Gọi d và d' lần lượt là khoảng cách từ một vật thật AB và từ ảnh A'B' của nó tới quang tâm O của thấu kính. Công thức thấu kính là $\frac{1}{d}+\frac{1}{d'}=\frac{1}{f}$

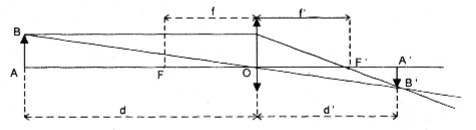
a) Tìm biểu thức xác định hàm số d' = f(d)

b) Tìm $\underset{d\rightarrow f^{+} }{lim}φ(d)$, $\underset{d\rightarrow f^{-} }{lim}φ(d)$ và $\underset{d\rightarrow +\infty }{lim}φ(d)$. Giải thích ý nghĩa của các kết quả tìm được

Phương pháp giải

a) Sử dụng công thức $\dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{f}$.

b) Sử dụng quy tắc tìm giới hạn của thương.

Hướng dẫn giải

a) Theo công thức thấu kính, ta có:

$\frac{1}{d'}=\frac{1}{f}-\frac{1}{d}\Leftrightarrow \frac{1}{d'}=\frac{d-f}{f.d}\Rightarrow d'=\frac{f.d}{d-f}$

Vậy hàm số cần tìm là $d'=\varphi (d)=\frac{f.d}{d-f}.$

b) $\lim_{d\rightarrow f^-}\varphi (d)=\lim_{d\rightarrow f^-} \frac{f.d}{d-f}=+\infty$

$\lim_{d\rightarrow 1^-}\varphi (d)=\lim_{d\rightarrow 1^-} \frac{f.d}{d-f}=-\infty$

$\lim_{d\rightarrow +\infty }\varphi (d)=\lim_{d\rightarrow +\infty} \frac{f.d}{d-f}=f.$