Giải bài tập SGK Toán 11 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song

Cho tứ diện ABCD. Gọi P, Q, R và S là bốn điểm lần lượt lấy trên bốn cạnh AB, BC, CD và DA. Chứng minh rằng nếu bốn điểm P, Q, R và S đồng phẳng thì:

a) Ba đường thẳng PQ, SR và AC hoặc song song hoặc đồng quy.

b) Ba đường thẳng PS, RQ và BD hoặc song song hoặc đồng quy.

Phương pháp giải:

a) Tìm ba mặt phẳng đôi một cắt nhau theo ba giao tuyến là PQ, SR và AC.

b) Tìm ba mặt phẳng đôi một cắt nhau theo ba giao tuyến là PS, RQ và BD.

Hướng dẫn giải:

a) Ta có:

PQ = (ABC) ∩ (PQRS).

RS = (PQRS) ∩ (ACD).

AC = (ABC) ∩ (ACD).

Vậy hoặc PQ, RS, AC đồng qui hoặc song song.

b) Ta có:

PS =(ABD) ∩ (PQRS).

RQ = (BCD) ∩ (PQRS).

BD = (ABD) ∩ (CBD).

Vậy PS, RQ, BD hoặc đồng quy hoặc song song.

Cho tứ diện ABCD và ba điểm P, Q, R lần lượt lấy trên ba cạnh AB, CD, BC. Tìm giao điểm S của AD và mặt phẳng (PQR) trong hai trường hợp sau đây.

a) PR song song với AC;

b) PR cắt AC.

Phương pháp giải:

a) Tìm giao tuyến của hai mặt phẳng chứa lần lượt hai đường thẳng PR và AC. S chính là giao điểm của giao tuyến đó với AD.

b) Tìm ba mặt phẳng cắt nhau đôi một theo ba giao tuyến phân biệt là PR, AC và giao tuyến thứ ba.

→ S chính là giao điểm của giao tuyến thứ ba với AD.

Hướng dẫn giải:

a) 

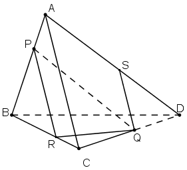
\(\left\{ \begin{array}{l} PR//AC\\ PR \subset \left( {PQR} \right)\\ AC \subset \left( {ACD} \right)\\ \end{array} \right.\)

\( \Rightarrow \left( {PQR} \right) \cap \left( {ACD} \right) = Qt\) là đường thẳng song song với AC và PR.

Gọi S là giao điểm của Qt và AD.

Vậy \(AD \cap (PQR) = S\).

b)

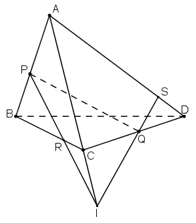
Gọi I là giao điểm của PR và AC. Ta có:

(ABC) ∩ (PQR) = PR (1).

(ACD) ∩ (ABC) = AC (2).

(ACD) cắt (PQR) (vì Q = (ACD) ∩ (PQR)) (3).

Từ (1), (2), (3) ⇒ PR, AC và giao tuyến của (ACD) và (PQR) đồng quy.

Mà PR ∩ AC = I

⇒ I ∈ (ACD) ∩ (PQR).

⇒ (ACD) ∩ (PQR) = QI.

Trong (ACD), gọi S là giao điểm của IQ và AD.

Vậy \(AD \cap (PQR) = S\).

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và G là trung điểm của đoạn MN.

a) Tìm giao điểm A’ của đường thẳng AG và mặt phẳng (BCD).

b) Qua M kẻ đường thẳng Mx song song với AA’ và Mx cắt (BCD) tại M’. Chứng minh B, M', A' thẳng hàng và BM' = M'A' = A'N.

c) Chứng minh GA = 3GA’.

Phương pháp giải:

a) Tìm một đường thẳng trong (BCD) cắt được AG

⇒ Giao điểm A' chính là giao điểm của AG và đường thẳng đó.

b)

- Chứng minh ba điểm B, M', A' cùng thuộc giao tuyến của hai mặt phẳng (ABN) và (BCD).

- Chứng minh A' là trung điểm của M'N, M' là trung điểm của A'B.

c) Áp dụng tính chất đường trung bình của tam giác: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

Hướng dẫn giải:

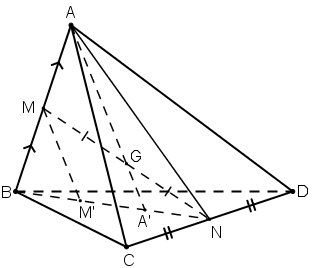
a) Ta có: MN ⊂ (ABN) ⇒ G ∈ (ABN) ⇒ AG ⊂ (ABN).

Trong (ABN), gọi A’ là giao điểm của AG và BN, ta có:

\(\left\{ \begin{array}{l} A' \in {\rm{ }}BN \subset \left( {BCD} \right)\\ A' \in AG{\rm{ }} \end{array} \right. \Rightarrow A' = AG \cap \left( {BCD} \right)\)

b) Ta có:

\(\left\{ \begin{array}{l} Mx//AA' \subset \left( {ABN} \right)\\ M \in \left( {ABN} \right) \end{array} \right. \Rightarrow Mx \subset \left( {ABN} \right)\)

Lại có: M’ = Mx ∩ (BCD) (giả thiết).

⇒ M’ nằm trên giao tuyến của (ABN) và (BCD).

Mà (ABN) ∩ (BCD) = BN.

⇒ B; M’; A’ thẳng hàng.

Xét tam giác NMM' có:

\(\left\{ \begin{array}{l} G \ là \ trung \ điểm \ của \ NM\\ GA'//MM' \end{array} \right. \Rightarrow A' \ là \ trung \ điểm \ của \ NM' \ (1).\)

Xét tam giác BAA' có:

\(\left\{ \begin{array}{l} M \ là \ trung \ điểm \ của \ AB\\ MM'//AA' \end{array} \right. \Rightarrow M' \ là \ trung \ điểm \ của \ BA' \ (2).\)

Từ (1) và (2) suy ra BM' = M'A' = A'N.

c) Ta có: MM' = \(\frac{1}{2}\) AA'.

GA' = \(\frac{1}{2}\) MM' = \(\frac{1}{2}\).\(\frac{1}{2}\) AA' = \(\frac{1}{4}\) AA'.

GA = AA' \(-\) GA' = AA' \(-\) ​\(\frac{1}{4}\)​ AA' = ​\(\frac{3}{4}\)​ AA'.

Suy ra GA = 3 GA'.